difficult
- 4. 寻找两个正序数组的中位数
- 41. 缺失的第一个正数
- 用数组下标作为哈希表
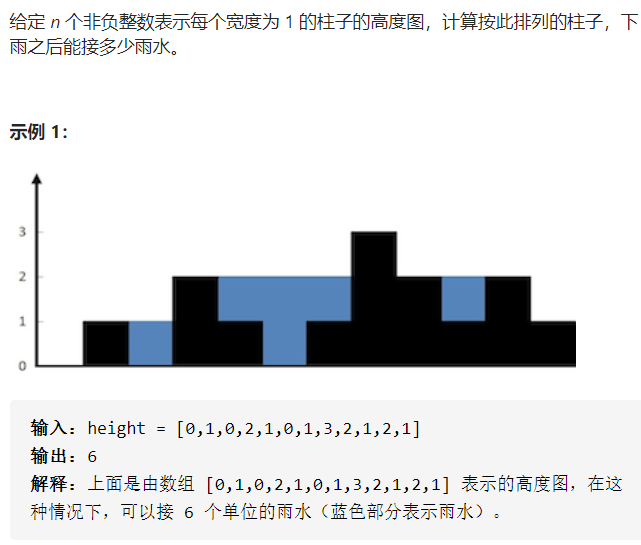
- 42.接雨水
- 单调栈
- 自己定义一个struct的优先队列
4. 寻找两个正序数组的中位数
给定两个大小为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。
进阶:你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗?
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
示例 3:
输入:nums1 = [0,0], nums2 = [0,0]
输出:0.00000
示例 4:
输入:nums1 = [], nums2 = [1]
输出:1.00000
示例 5:
输入:nums1 = [2], nums2 = []
输出:2.00000
浩浩的题解更清楚
41. 缺失的第一个正数
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
进阶:你可以实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案吗?
示例 1:
输入:nums = [1,2,0]
输出:3
示例 2:
输入:nums = [3,4,-1,1]
输出:2
示例 3:
输入:nums = [7,8,9,11,12]
输出:1
用数组下标作为哈希表
对于一个长度为 NN 的数组,其中没有出现的最小正整数只能在 [1, N+1]中。这是因为如果[1,N] 都出现了,那么答案是 N+1,否则答案是[1,N] 中没有出现的最小正整数。
我们对数组进行遍历,对于遍历到的数 x,如果它在 [1, N][1,N] 的范围内,那么就将数组中的第 x-1 个位置(注意:数组下标从 0 开始)打上「标记」。在遍历结束之后,如果所有的位置都被打上了标记,那么答案是 N+1,否则答案是最小的没有打上标记的位置加 1。
class Solution {
public:
int firstMissingPositive(vector<int>& nums) {
for(int i=0;i<nums.size();i++)
{
if(nums[i]<=0)
nums[i]=nums.size()+3;//将数组中所有小于等于 00 的数修改为 N+3
}
for(int i=0;i<nums.size();i++)
{
if(abs(nums[i])<=nums.size())
nums[abs(nums[i])-1]=-1*abs(nums[abs(nums[i])-1]);
//遍历数组中的每一个数 x,它可能已经被打了标记,因此原本对应的数为 |x|,其中∣∣为绝对值符号。如果 ∣x∣∈[1,N],那么我们给数组中的第 |x| - 1个位置的数添加一个负号。注意如果它已经有负号,不需要重复添加
}
for(int i=0;i<nums.size();i++)
{
if(nums[i]>0)
return i+1;//在遍历完成之后,如果数组中的每一个数都是负数,那么答案是 N+1,否则答案是第一个正数的位置加 1
}
return nums.size()+1;
}
};
42.接雨水
class Solution {
public:
int trap(vector<int>& height) {
int result=0;
vector<int> maxleft(height),maxright(height);
for(int i=height.size()-2;i>=0;i--)
maxright[i]=max(maxright[i],maxright[i+1]);
for(int i=1;i<height.size();i++)
{
maxleft[i]=max(maxleft[i-1],maxleft[i]);
result+=(min(maxleft[i],maxright[i])-height[i]);
}
return result;
}
};
单调栈
就是,比栈顶小/大才放进去
int trap(vector<int>& height)
{
int ans = 0, current = 0;
stack<int> st;
while (current < height.size()) {
while (!st.empty() && height[current] > height[st.top()]) {
int top = st.top();
st.pop();
if (st.empty())
break;
int distance = current - st.top() - 1;
int bounded_height = min(height[current], height[st.top()]) - height[top];
ans += distance * bounded_height;
}
st.push(current++);
}
return ans;
}
自己定义一个struct的优先队列
struct Status {
int val;
ListNode *ptr;
bool operator < (const Status &rhs) const {
return val > rhs.val;
}
};
priority_queue <Status> q;
ListNode* mergeKLists(vector<ListNode*>& lists) {
for (auto node: lists) {
if (node) q.push({node->val, node});
}
}
最后
以上就是细心蓝天最近收集整理的关于leetcode困难题题解top的全部内容,更多相关leetcode困难题题解top内容请搜索靠谱客的其他文章。








发表评论 取消回复