文章目录
- 二叉搜索树
- 中序遍历(Inorder)
- 插入节点
- 查找节点
- 删除节点:
- key/value模型
- 实现中英文翻译
- 翻译效果
- 修改节点
二叉搜索树
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
int a [] = {5,3,4,1,7,8,2,6,0,9};
使用价值:搜索
template <class K>//为了统一类型
二叉树包含左子树和右子树和值:并且希望哪里都可以访问,我们定义一个结构体struct BSTNode默认是公有访问
template <class K>
struct BSTNode
{
BSTNode<K>*_right;
BSTNode<K> *_left;
K _key;
};
然后开始创建对象class BSTree,为了方便typedef BSTNode Node * _root;简写成typedef BSTNode<K> Node; Node* _root;整体框架:
class BSTree
{
typedef BSTNode<K> Node;
public:
BSTree() :_root(nullptr)
{}
private:
Node* _root;
};
增删查改接口:
void InOrder(){}//中序遍历
bool Insert(const K&key){}
Node*find(const K&key){}
bool Erase(const K &key){}
中序遍历(Inorder)
这里为了可以在类里面访问私有成员变量,我们写一个方法把_root传参_:
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node*root)
{
if (root == nullptr)
return;
//中序遍历
_InOrder(root->_left);
cout << root->_key<< " ";
_InOrder(root->_right);
}
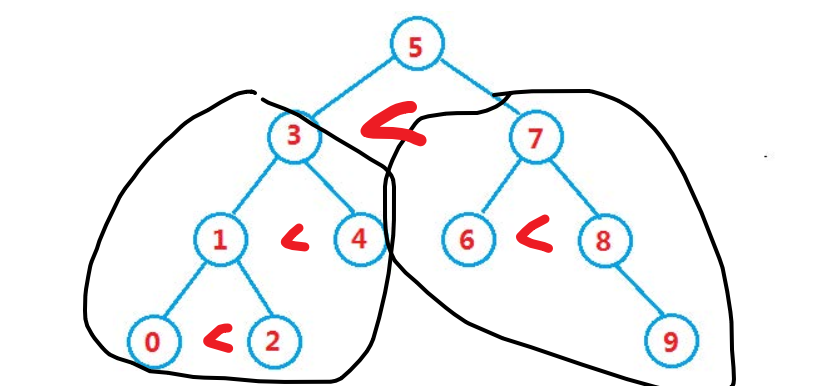
根据完全二叉树的特性,可以把数组5, 3, 4, 1, 7, 8, 2, 6, 0, 9构成下图逻辑结构:
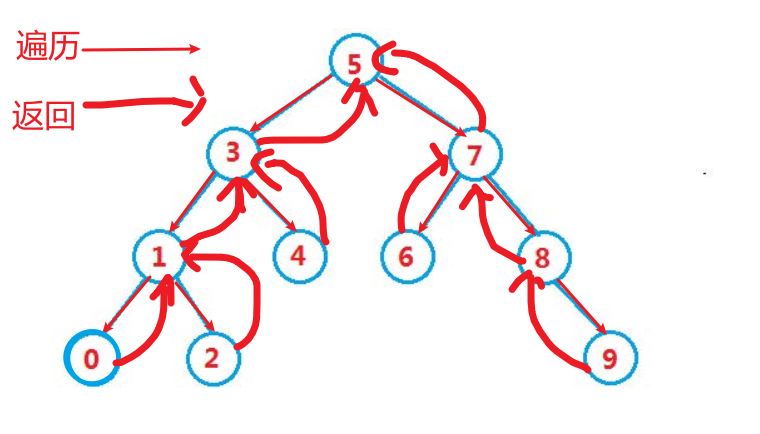
中序的遍历规则是:先遍历左孩子然后是父亲最后是右孩子
插入节点
插入第一个节点,根节点现在为空,判断一下,如果是第一次插入就是根节点:
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
这里用了new 开辟空间,需要自己写一个构造函数并初始化
BSTNode(const K& key)
:_right(nullptr)
, _left(nullptr)
, _key(key)
{}
我们需要有个节点cur指向根节点Node* cur = _root;
对cur指向的值进行判断是否比插入的节点小,根据二叉搜索树特性,左孩子小于右孩子;如果cur指向的值比新插入的小,那我们cur指向右孩子cur = cur->_right;,如果cur指向的值比新插入的大,那我们cur指向左孩子cur = cur->_left;,最后一种就是它们相等,那就返回假;
while(cur)
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key>key)
{
cur = cur->_left;
}
else
{
return false;
}
}
左孩子和右孩子已经分出来了,那结合起来的它们父亲该谁做呢?我们就需要定义一个父亲:Node*parent = nullptr;,并判断父亲指向的值是大还是小
Node* cur = _root;
Node*parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key>key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
parent->_right = cur;
else
{
parent->_left = cur;
}
return true;
查找节点
查找很简单,通过比大小,大的在右边,小的在左边:
Node*find(const K&key)
{
Node*cur = _root;
while (cur)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
return cur;
}
return NULL;
}
删除节点:
我们删除节点需要找到那个节点,那怎么找呢?这里我们也和插入一样使用用双指针,通过cur指向的节点可以找到父亲和左右孩子,但是删除有3种情况:

解决方案:
1:删除自己,父亲指向自己位置的指针置空
2:删除节点,把孩子交给父亲,顶替自己的位置
3:替换法删除。去孩子里面找一个值能替换自己位置的节点,替换自己删除

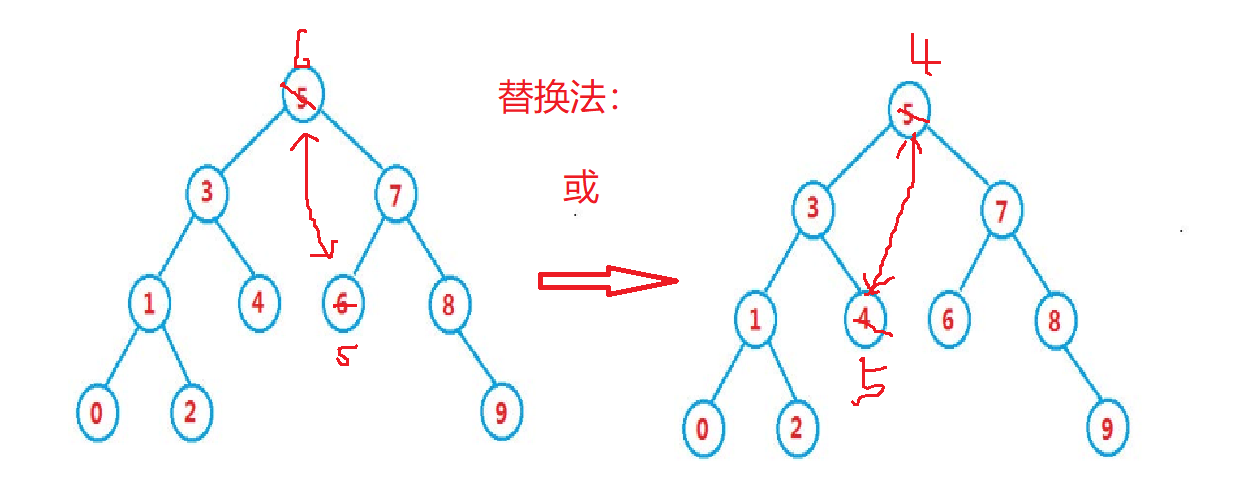
第一种情况:删除8,我们需要通过8这个值找到父亲,并判断父亲指向这个值是左孩子还是右孩子,看图8这个父亲有个右孩子9,删除8之后,右孩子8的父亲也要指向右孩子9

第二种就是相反:
第三种就需要找删除树的最小的节点,我们假设在右子树,我们也定义两个指针,一个是最小值的父亲和最小值的右子树Node* minParent = cur;Node* minRight = cur->_right;,当然最小的一个节点一定是在最左边
while (minRight->_left)
{
minRight = minRight->_left;
}
找到最小的值后 和删除的值替换
cur->_key = minRight->_key;//替换
//删除替换节点
if (minParent->_left == minRight)//如果父亲有左孩子
minParent->_left = minRight->_right;
else//如果是右孩子
minParent->_right = minRight->_right;
delete minRight;
删除测试:
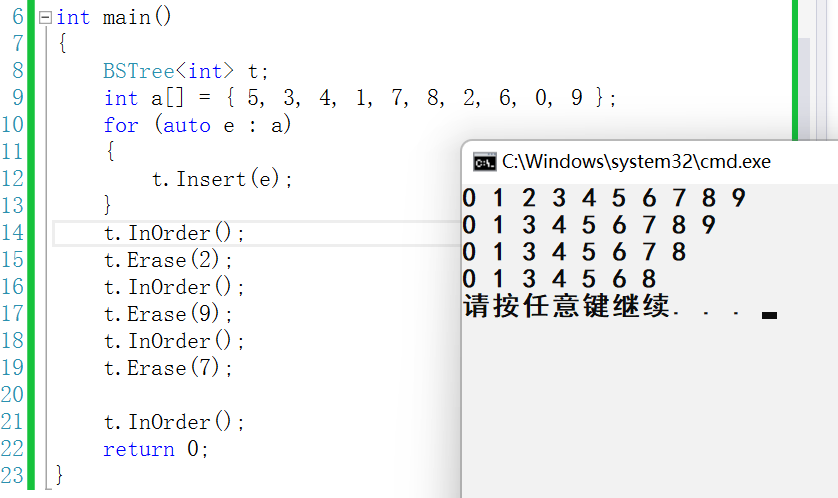
但是仔细一看会有一个bug:那就是全部删除之后,我们没有处理为空树的情况会怎么样;
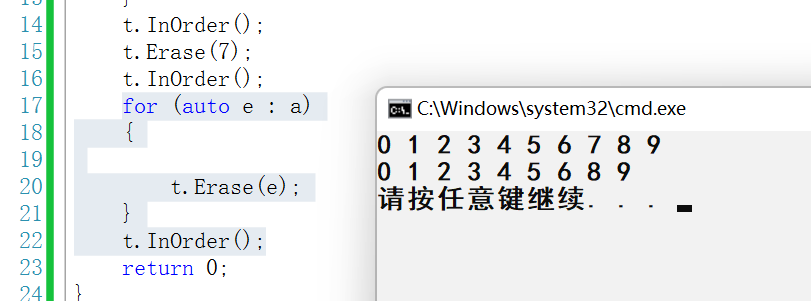
我们需要在前面判断,要是删除到根节点,就让根节点指向左子树还是右子树
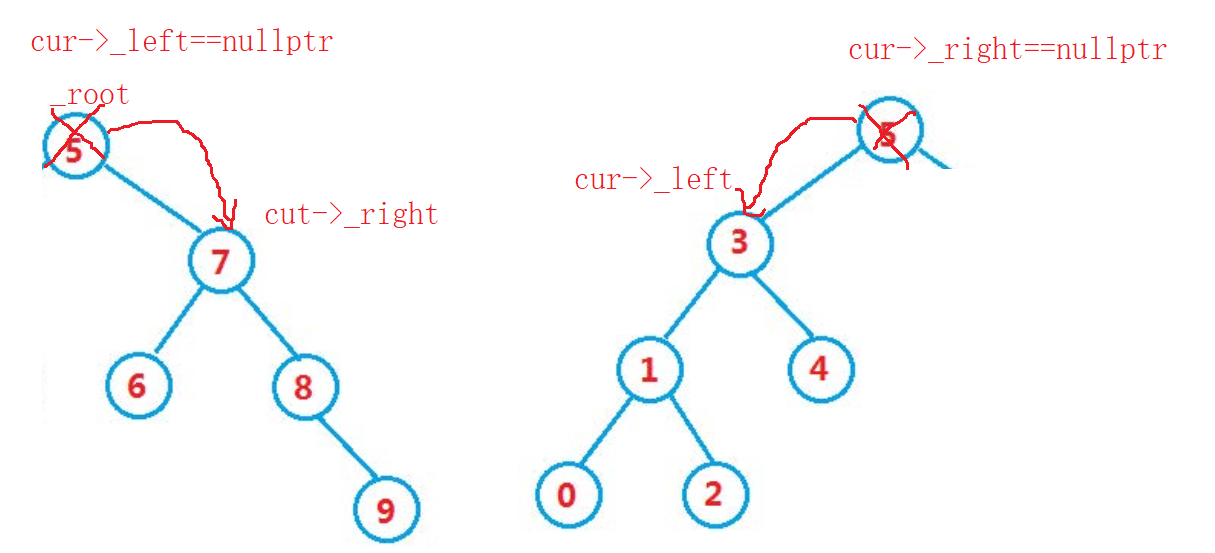
//找到了,准备删除
if (cur->_left == nullptr)//左为空
{
if (cur == _root)
{
_root=cur->_right;//指向右树
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
parent->_right = cur->_right;
}
delete cur;
}
else if (cur->_right == nullptr)//右为空
{
if (cur == _root)
{
_root = cur->_left;//指向左树
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
parent->_right = cur->_right;
}
key/value模型

我们再加一个模板class V
template <class K,class V>
实现中英文翻译
template <class K,class V>
struct BSTNode
{
BSTNode<K,V>*_right;
BSTNode<K,V> *_left;
K _key;
V _value;
BSTNode(const K& key,const V& value)
:_right(nullptr)
, _left(nullptr)
, _key(key)
, _value(value)
{}
};
template <class K,class V>
class BSTree
{
typedef BSTNode<K,V> Node;
public:
BSTree() :_root(nullptr)
{}
Node* Insert(const K&key,const V&value)
{
if (_root == nullptr)
{
_root = new Node(key,value);
return nullptr;
}
Node* cur = _root;
Node*parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key>key)
{
parent = cur;
cur = cur->_left;
}
else
{
return nullptr;
}
}
cur = new Node(key,value);
if (parent->_key < key)
parent->_right = cur;
else
parent->_left = cur;
return cur;
}
Node*find(const K&key)
{
Node*cur = _root;
while (cur)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
return cur;
}
return NULL;
}
bool Erase(const K &key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key>key)
{
parent = cur;
cur = cur->_left;
}
else
{
//找到了,准备删除
if (cur->_left == nullptr)//左为空
{
if (cur == _root)
{
_root=cur->_right;//指向右树
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
parent->_right = cur->_right;
}
delete cur;
}
else if (cur->_right == nullptr)//右为空
{
if (cur == _root)
{
_root = cur->_left;//指向左树
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
parent->_right = cur->_right;
}
}
else
{
//找到右子树的最小节点
Node* minParent = cur;//这里不能等于nullprt,当cur的右节点没有左孩子,循环不进去,删除替换节点就会出错
Node* minRight = cur->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
cur->_key = minRight->_key;//替换
//删除替换节点
if (minParent->_left == minRight)//如果父亲有左孩子
minParent->_left = minRight->_right;
else//如果是右孩子
minParent->_right = minRight->_right;
delete minRight;
}return true;
}
}return false;
}
void _InOrder(Node*root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key<< " ";
_InOrder(root->_right);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
Node* _root=nullptr;
};
翻译效果
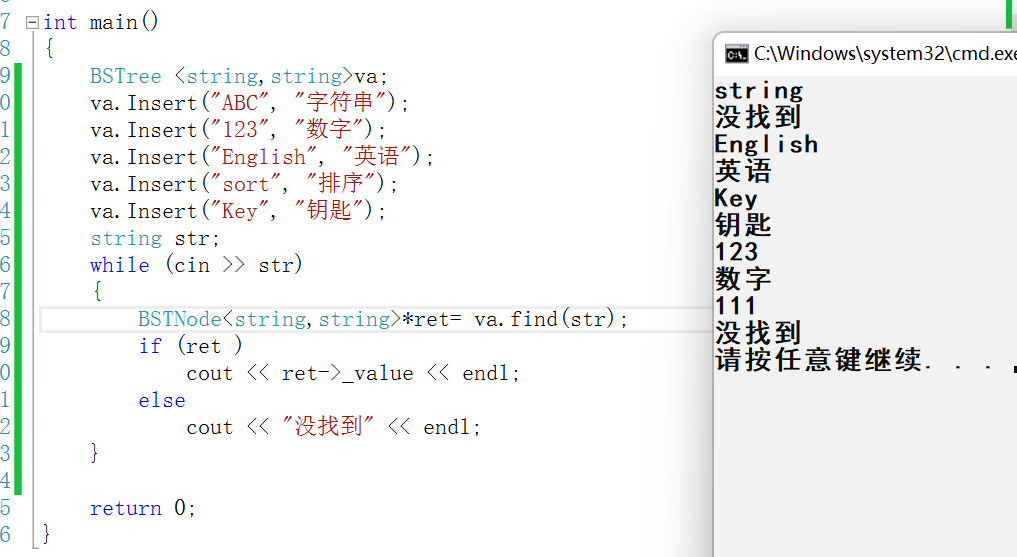
修改节点
知道为什么才开始修改节点吗?因为我们可以通过K/V模型修改,Key是不能修改的;假设修改根节点值为0,那树的结构全乱了,但是有了value值后可以对它进行修改,
- 如果对大家有帮助,请三连支持一下!
- 有问题欢迎评论区留言,及时帮大家解决!
最后
以上就是畅快山水最近收集整理的关于C++之二叉树进阶|搜索树|key/value模型二叉搜索树的全部内容,更多相关C++之二叉树进阶|搜索树|key/value模型二叉搜索树内容请搜索靠谱客的其他文章。








发表评论 取消回复