朱金灿
假如我们采用矢量表达式来表示参数化的二次曲线,那么可以把抛物线的表达式写成如下的一般形式:
P(t)=A1+ A2t+ A3t2 (0=<t<=1)
该抛物线过P1, P2, P3三个点,并且:
1. 抛物线以P1点为始点。当参变量t=0时,曲线过P1点;
2. 抛物线以P3点为终点。当参变量t=0时,曲线过P3点;
3. 当参变量t=0.5时,曲线过P2点,且切矢量等于P3—P1。
t=0: P(0)= A1= P1
t=1: P(1)= A1 + A2+ A3=P3
t=0.5:P(0.5)= A1 + 0.5A2+0.25 A3=P2
通过解联立方程,得到三个参数A1 、 A2、 A3分别为:
A1 = P1
A2=4 P2—P3—3P1
A3=2P1+2P3—4P2
把求出的这三个系数的值,代入抛物线的表达式P(t)=A1+ A2t+ A3t2
得:P(t)=(2t—3t+1)P1 +(4t—4t2)P2+(4t2—t)P3 (0=<t<=1)
设有一离散型值点列Pi(i=1,2,……,n),每经过相邻三点作一段抛物线,由于有n个型值点,所以可以做n-2条抛物线段。
在这n—2条抛物线段中,第i条抛物线段为经过Pi, Pi+1, Pi+2三点,所以它的表达式应为:Si(ti)=(2t2i—3ti+1)Pi +(4 ti—4 t2i) Pi+1 +(2t2i—ti) Pi+2 (0=< ti <=1)
同理,第i+1条抛物线段为经过Pi+1, Pi+2, Pi+3三点,所以它的表达式应为:Si+1(ti+1)=(2t2i+1—3ti+1+1)Pi+1 +(4 ti+1—4 t2i+1) Pi+2 +(2t2i+1—ti+1) Pi+3 (0=< ti+1 <=1)
一般来说,每两段曲线之间的搭接区间,两条抛物线是不可能重合的。如下图所示:
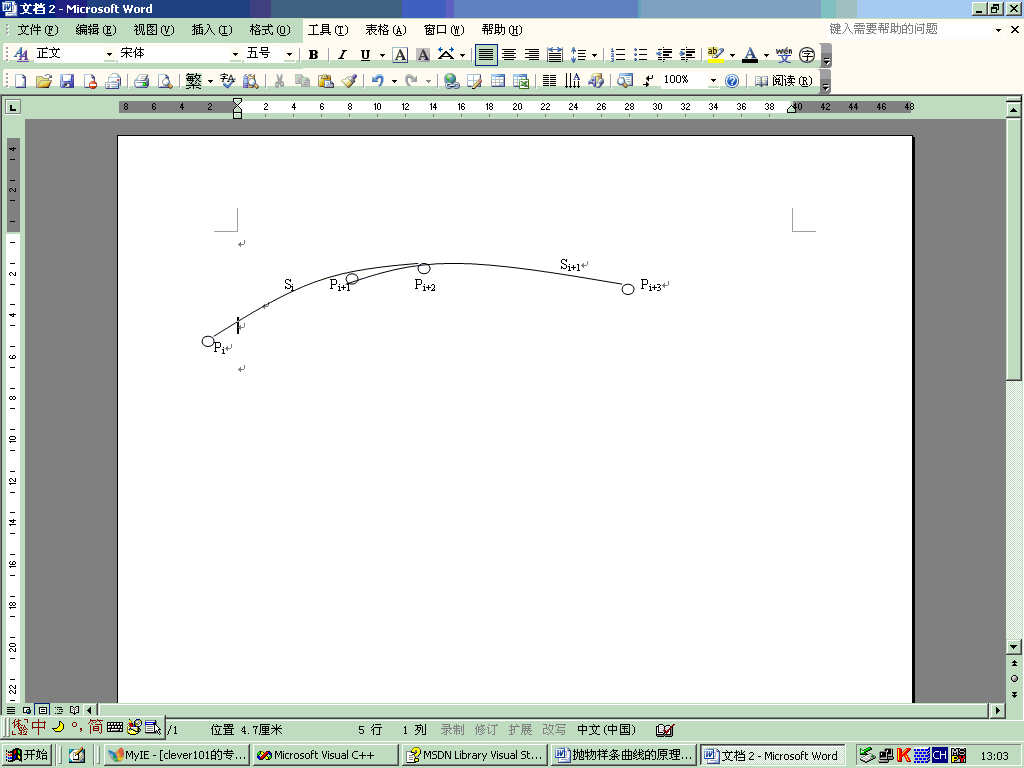
显然,对于拟合曲线来说,整个型值点必须只能用一条光滑的曲线连接起来。为了做到这一点,必须找一种方法把Si和Si+1 这样的曲线段的共同区间结合起来。这种方法就是加权合成方法。
我们设共同区间的函数是Pi+1(t)=f (T ) Si(ti)+g ( T) Si+1(ti+1). 其中f (T ) 和 g ( T) 是权函数。在抛物样条曲线中我们取简单的一次函数为权函数,且具有互补性,设
f (T ) =1—T
g ( T) =T
这样Pi+1(t)= (1—T ) Si(ti)+ T Si+1(ti+1).因为 函数中有T、ti和ti+1三个参数,因此接下来我们的工作是统一参数。我们可以三个参变量统一形式为:
T=2t
ti=0.5+t
ti+1=t
这样Pi+1(t)= (—2t3+4t2—t)Pi +(12t3—410t2+1) Pi+1 +(—12t3+8t2+t) Pi+2 +(4t3—2t2) Pi+3 (0=< ti <=0.5)
从几何意义上说,函数Pi+1(t)表示的上图的点Pi+1,到Pi+2 之间的线段。但是我们应该看到这种方法从n个点中只能得到n—3段曲线。但是n个型值点应有n—1段曲线。一个直接的想法是添加两个辅助点。那么如何添加呢?
方法一:两个辅助点为P0和Pn+1, P0=P1,Pn+1= Pn ,这样画出的曲线为一条不闭合的自由曲线。
方法二:添加三个辅助点,P0、Pn+1和Pn+2,然后P0=Pn,Pn+1= P1, ,Pn+2= P2,这样画出的曲线为一条闭合的曲线。
下面介绍根据上面原理而设计的一个画抛物曲线的一个类:
class CParspl : public CObject
{
DECLARE_SERIAL(CParspl)
public:
CParspl(int nLineStyle,int nLineWidth, COLORREF crLineColor);
virtual ~CParspl();
void SetPoint(const CPoint &point); // 添加坐标点
void DrawFreeLine(CDC *pDC);// 画自由端抛物曲线
void DrawCloseLine(CDC *pDC); // 画封闭端抛物曲线
void Serialize(CArchive & ar);
protected:
CParspl();
/*public attributes*/
public:
int m_bIsFreeLine;
/*private attibutes*/
private:
CArray<CPoint,CPoint> ParsplPoint; // 定义插值点数组
COLORREF m_crLineColor; // 定义线色
int m_nLineStyle; // 定义线型
int m_nLineWidth; //定义线宽
};
const int Clip=10;
CParspl::CParspl() // 默认的构造函数
{
}
CParspl::~CParspl()
{
}
CParspl::CParspl(int nLineStyle,int nLineWidth, COLORREF crLineColor)
{
m_nLineStyle = nLineStyle;
m_nLineWidth = nLineWidth;
m_crLineColor = crLineColor;
ParsplPoint.Add(CPoint(0,0)); //初始化第一个点
m_bIsFreeLine = 1;
}
void CParspl::SetPoint(const CPoint &point)
{
ParsplPoint.Add(point);
}
void CParspl::DrawFreeLine(CDC *pDC)
{
if(ParsplPoint.GetSize() < 4) return;
CPen LinePen(m_nLineStyle,m_nLineWidth,m_crLineColor);
int i=0,j=0;
int n=0;
n=ParsplPoint.GetSize();
double t1,t2,t3,t,a,b,c,d,x,y;
ParsplPoint[0].x=ParsplPoint[1].x;
ParsplPoint[0].y=ParsplPoint[1].y;
CPoint pt=ParsplPoint.GetAt(n-1);
ParsplPoint.Add(pt);
t= 0.5f /Clip;
CPen *pLinePen=pDC->SelectObject(&LinePen);
pDC->MoveTo(ParsplPoint[1].x,ParsplPoint[1].y);
for (i=0;i<n-2;i++)
{
for(j=1;j<Clip;j++)
{
t1=j*t;
t2=t1*t1;
t3=t2*t1;
a=4.0*t2-t1-4.0*t3;
b=1.0-10.0*t2+12.0*t3;
c=t1+8.0*t2-12.0*t3;
d=4.0*t3-2.0*t2;
x=a*ParsplPoint[i].x+b*ParsplPoint[i+1].x+c*ParsplPoint[i+2].x+d*ParsplPoint[i+3].x;
y=a*ParsplPoint[i].y+b*ParsplPoint[i+1].y+c*ParsplPoint[i+2].y+d*ParsplPoint[i+3].y;
pDC->LineTo(int(x),int(y));
}
pDC->LineTo(ParsplPoint[i+2].x,ParsplPoint[i+2].y);
}
for(i=0;i<n;i++)
{
pt=ParsplPoint.GetAt(i);
pDC->Ellipse(pt.x-2,pt.y-2,pt.x+2,pt.y+2);
}
/* 将旧画笔选回设备环境*/
pDC->SelectObject(pLinePen);
/*删除辅助点*/ ParsplPoint.RemoveAt(ParsplPoint.GetUpperBound());
}
void CParspl::DrawCloseLine(CDC *pDC)
{
if(ParsplPoint.GetSize() < 4) return;
CPen LinePen(m_nLineStyle,m_nLineWidth,m_crLineColor);
int i=0,j=0;
int n=0;
n=ParsplPoint.GetSize();
double t1,t2,t3,t,a,b,c,d,x,y;
ParsplPoint[0].x=ParsplPoint[n-1].x;
ParsplPoint[0].y=ParsplPoint[n-1].y;
CPoint pt=ParsplPoint.GetAt(1);
ParsplPoint.Add(pt);
pt=ParsplPoint.GetAt(2);
ParsplPoint.Add(pt);
t= 0.5f /Clip;
CPen *pLinePen=pDC->SelectObject(&LinePen);
pDC->MoveTo(ParsplPoint[1].x,ParsplPoint[1].y);
for (i=0;i<n-1;i++)
{
for(j=1;j<Clip;j++)
{
t1=j*t;
t2=t1*t1;
t3=t2*t1;
a=4.0*t2-t1-4.0*t3;
b=1.0-10.0*t2+12.0*t3;
c=t1+8.0*t2-12.0*t3;
d=4.0*t3-2.0*t2;
x=a*ParsplPoint[i].x+b*ParsplPoint[i+1].x+c*ParsplPoint[i+2].x+d*ParsplPoint[i+3].x;
y=a*ParsplPoint[i].y+b*ParsplPoint[i+1].y+c*ParsplPoint[i+2].y+d*ParsplPoint[i+3].y;
pDC->LineTo(int(x),int(y));
}
pDC->LineTo(ParsplPoint[i+2].x,ParsplPoint[i+2].y);
}
for(i=0;i<n;i++)
{
pt=ParsplPoint.GetAt(i);
pDC->Ellipse(pt.x-2,pt.y-2,pt.x+2,pt.y+2);
}
/*将旧画笔选回设备环境*/
pDC->SelectObject(pLinePen);
/*删除最后两个辅助点*/
ParsplPoint.RemoveAt(ParsplPoint.GetUpperBound());
ParsplPoint.RemoveAt(ParsplPoint.GetUpperBound());
}
程序效果图:
自由端曲线:
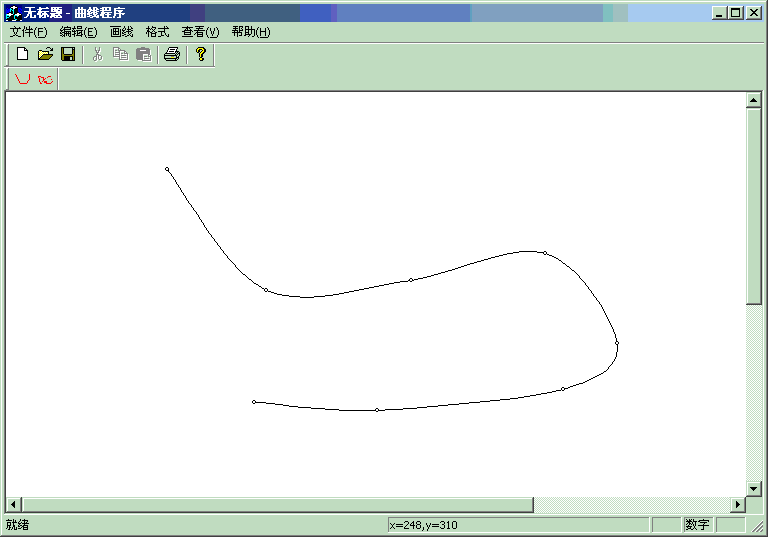
封闭端曲线:
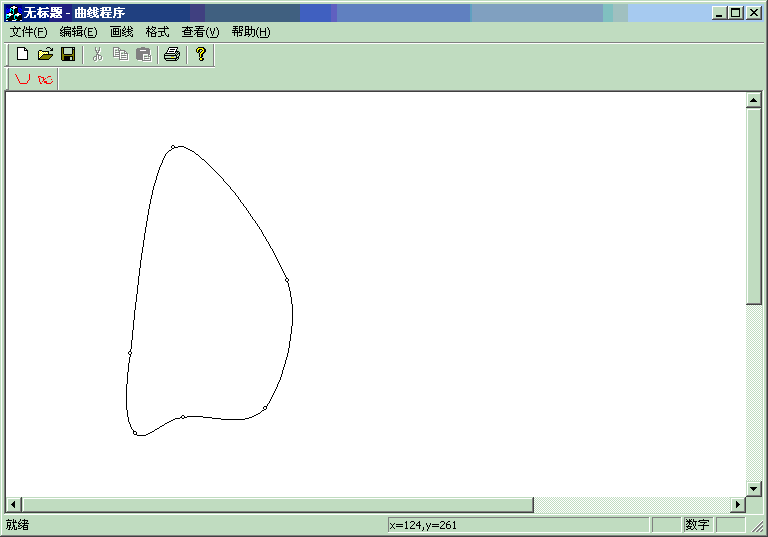
最后
以上就是冷艳白昼最近收集整理的关于抛物样条曲线的原理说明及画抛物曲线的一个类的全部内容,更多相关抛物样条曲线内容请搜索靠谱客的其他文章。

![[源码和文档分享]基于easyx实现的黑白棋游戏](https://www.shuijiaxian.com/files_image/reation/bcimg10.png)






发表评论 取消回复