1、向量

向量：对相似数据项的集合进行分组的最简单方式，向量是数据的一维分组。
元素：向量中放入数据项通常称为元素。
向量的创建：
1、直接输入数据，比如创建行向量

>> A = [1,2,3,4]

A =

     1     2     3     4

2、使用冒号的方式(起始值:增量:结束值)

>> A = 1:1:4

A =

     1     2     3     4

3、函数，比如linspace()、zeros(1,n), ones(1,n) 等等

>> ones(1,4)

ans =

     1     1     1     1

2、向量共线和共面的判断

向量共线和共面的判断：当3(两)个向量线性相关时，如果这3(两)个向量组成的秩小于3(2),那么这3(两)个向量共面(共线)，否则不共面(共线）。
matlab求秩的函数为rank()。

示例：	X = [1,5,6], Y = [-1,5,7], Z = [7,9,1]。判断这三个向量是否共面。
X = [1,5,6];
Y = [-1,5,7];
Z = [7,9,1];

A= [X;Y;Z];
rank(A)

ans =

     3
这三个向量的秩为3，所以这三个向量不共面。

3、向量方向余弦的计算

假设V = (x,y,z)是一个空间向量，r是v的长度，那么称向量D= (x/r, y/r,z/r)是向量V的方向余弦。这里使用norm(）函数->求向量的长度。

示例：设向量V1 = (1,2,3)，求方向余弦。
>> x = [1,2,3];
>> costhea = x/norm(x)

costhea =

    0.2673    0.5345    0.8018

4、向量的内积

定义：向量的内积也是数分中的“内积”.
a = [a1,a2,a3,…an];
b = [b1,b2,b3,…bn];
a*b = a1b1 + a2b2 + a3b3+ … + anbn;

几何意义:一个向量在另一个向量上的投影长度。

格式: dot(A,B);

已知:A = [1,2,3], B = [4,5,6], 求这两个向量的内积。

>> A = [1 2 3];
>> B = [4 5 6];
>> dot(A,B)

ans =

    32

%	1*4 + 2*5 + 3*6 = 32

5、向量的夹角

设U = (u1,u2,u3), V = (v1,v2,v3)是两个空间向量，r1,r2分别是U,V的长度，（U,V）= u1v1+ u2v2 + u3v3是U,V的内积，Θ是U,V的夹角，从解析几何中知道，向量内积与夹角的关系为（U,V）= r1r2cosΘ。这里使用一个新函数反余弦函数acos();

已知:A = [1,2,3], B = [4,5,6], 求这两个向量的夹角

>> A = [1 2 3];
>> B = [4 5 6];
>> r1 = norm(A);
>> r2 = norm(B);
>> costheta = dot(A,B)/(r1*r2);
>> theta = acos(costheta)*180/pi

theta =

   12.9332

6、两点之间的距离

设U = (u1,u2,u3), V = (v1,v2,v3)是两个空间点坐标，这两个向量差向量的长度就是 两点之间的距离。

已知:A = [1,2,3], B = [4,5,6], 求这两个点之间的距离

>> A = [1 2 3];
>> B = [4 5 6];
>> norm(A-B)

ans =

    5.1962

6、向量的向量积（叉积）

几何意义：表示过两相交向量的交点，垂直于两向量所在平面的向量。
数据表达式:
1、|c| = |a*b|sin<a,b>
2、c ⊥ a,并且c ⊥ b
3、c的方向要用"右手法则" 判断

格式: cross(a,b)

已知:A = [1,2,3], B = [4,5,6], 求这两个向量的叉积
>> A = [1 2 3];
>> B = [4 5 6];
>> cr = cross(A,B)

cr =

    -3     6    -3


可以用dot来进行验证
>> dot(A,cr)

ans =

     0

7、向量的混合积

定义：假设a,b,c是空间中三个向量，则(ab).c称为a,b,c的混合积。
(ab).c = |ab||c|cos(ab,c)
几何意义:它的绝对值表示以向量为棱的平行六面体的体积

格式：
dot(cross(a,b).c);
dot(a,cross(b,c));

已知:U = [0,0,2], V = [3,0,5], W = [1,1,0]。求这两个向量的叉积
>> U = [0 0 2];
>> V = [3 0 5];
>> W = [1 1 0];
>> dot(cross(U,V),W)

ans =

     6

8、点到平面的距离

定义：设U = (u1,u2,u3) 到平面Ax+By+Cz+D=0的距离r 的计算公式为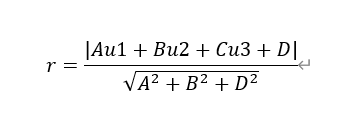

例：求原点到平面5.8x-4.5y+3.9z=1.78的距离

>> O = [0 0 0];
>> V = [5.8 -4.5 3.9];
>> dis = abs(dot(O,V)-1.78)/norm(V)

dis =

    0.2141

最后

以上就是苗条高跟鞋为你收集整理的Matlab 向量的处理1、向量2、向量共线和共面的判断3、向量方向余弦的计算4、向量的内积5、向量的夹角6、两点之间的距离6、向量的向量积（叉积）7、向量的混合积8、点到平面的距离的全部内容，希望文章能够帮你解决Matlab 向量的处理1、向量2、向量共线和共面的判断3、向量方向余弦的计算4、向量的内积5、向量的夹角6、两点之间的距离6、向量的向量积（叉积）7、向量的混合积8、点到平面的距离所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。