新版本Matlab中行列向量相加的机制

最近,我在用MATLAB画一个三维图的时候,发现了MATLAB中行向量与列向量相加的神奇机制.

在使用MATLAB画三维图时,函数要求因变量z必须为一个行与列都与x,y严格相关的矩阵.一般都是用meshgrid函数生成两个维数相同的矩阵后,在此基础上算出z.但由于我初学MATLAB 一开始不知道meshgrid函数和z的要求,一阵骚操作发现了和meshgrid等效的一个方法.

定义了一个1x2向量X和一个1x3向量Y.

meshgrid函数把X这个行向量复制出了length(Y)份后组装成一个矩阵赋给了X_new,又把Y转置为列向量后复制出了length(X)份后组装成一个矩阵赋给了Y_new.最终得到的两个新的矩阵均为3x2矩阵,行数与length(Y)相等,列数与length(X)相等.

再让X与Y相加后得到Z.

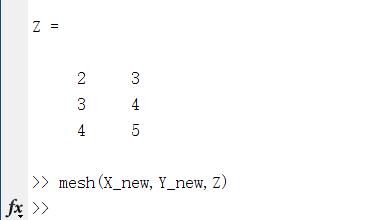
这样就能利用mesh函数画出三维图了.

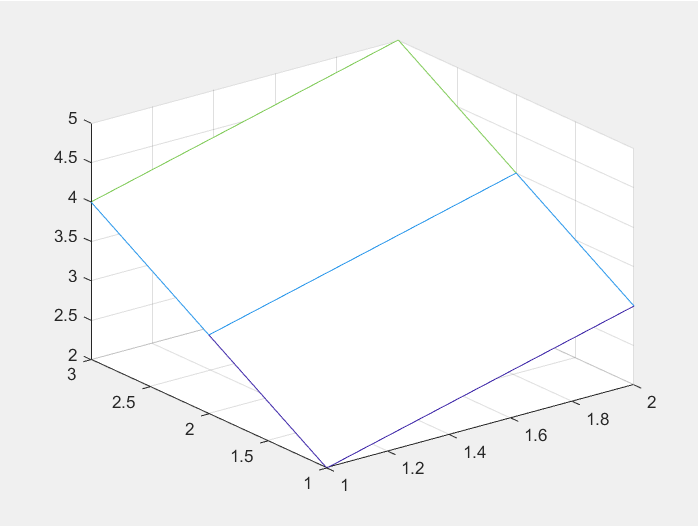
而当我直接令Z = X+Y’时,得到的Z居然和通过meshgrid方法最终得到的Z一样.

并且可生成与meshgrid方法一样的三维图

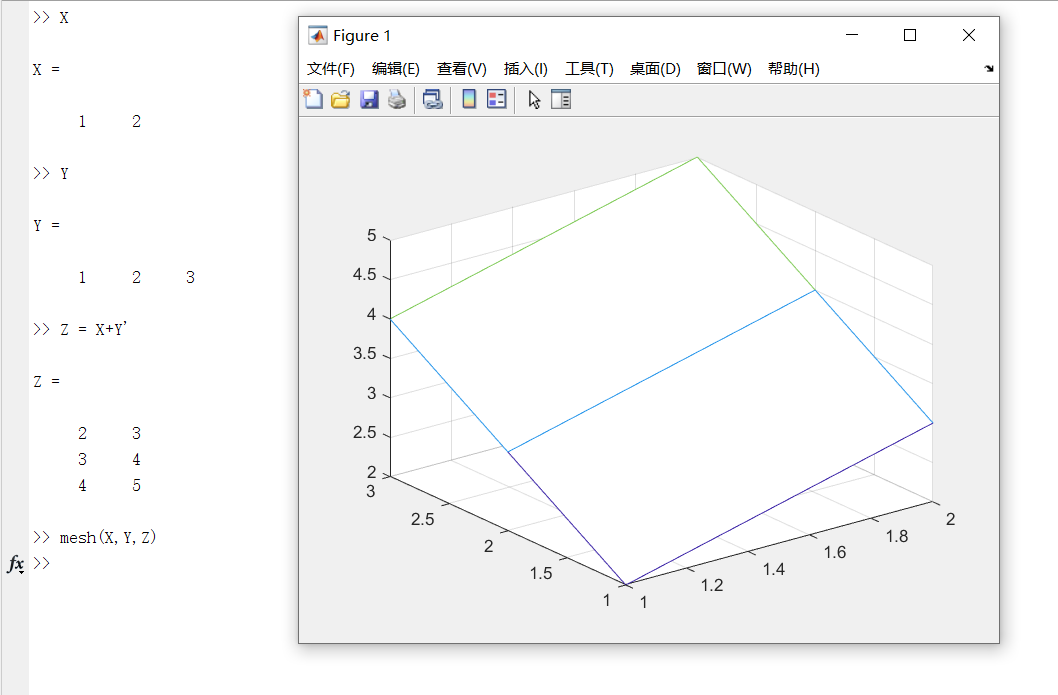
询问老师后得知,旧版本(2018之前)的MATLAB是没有这个机制的.在新版本中,只要让行列向量相加,行向量扩充为length(列向量)个,每一行的每个元素都会加上列向量中对应行的那个数.

如下图,Z = X’+Y

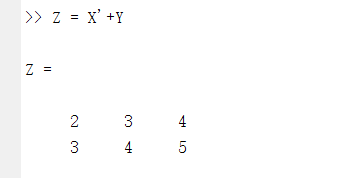
需注意的是若想利用此方法直接得到能画出三维图的Z,需要转置第二个行向量(Y).转置第一个行向量(X)得到的结果与meshgrid不一样,也不符合mesh函数的要求.

本文仅记录笔者的一个发现,还是建议大家用meshgrid函数.

最后

以上就是善良老鼠为你收集整理的新版本Matlab中行列向量相加的机制的全部内容，希望文章能够帮你解决新版本Matlab中行列向量相加的机制所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。