0. 引言

    最近在学习器件的噪声表征，涉及到了噪声的功率谱密度曲线，但这条曲线代表了啥意思？查了一下，用到了傅里叶变换。但为啥要这么搞？傅里叶变换背后真正的物理意义又是什么？
    为了了解这其中的根源，补了一下信号与系统的知识，在b站发现了西电郭宝龙老师的宝藏课程，讲解的可以说是很透彻了，非常适合零基础入门，以下是对傅里叶变换部分进行的简单梳理。

1. 广义傅里叶级数

1.1 矢量的正交分解

1.1.1 二维空间的矢量正交分解

    二维空间中，矢量$V$可以表示为正交矢量$V_1$和$V_2$的线性组合，$\overrightarrow{V}=c_1\overrightarrow{V_1}+c_2\overrightarrow{V_2}$，如下图所示。

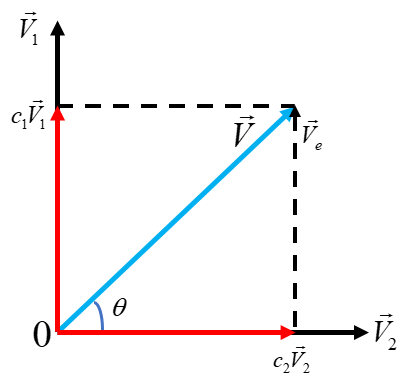
    其中
$$c_2=\frac{\left|\overrightarrow{V}\right|\cdot \cos \theta }{\left|\overrightarrow{V_2}\right|}=\frac{\left|\overrightarrow{V}\right|\cdot \left|\overrightarrow{V_2}\right|\cos \theta }{\left|\overrightarrow{V_2}\right|\cdot \left|\overrightarrow{V_2}\right|}=\frac{\overrightarrow{V}\cdot \overrightarrow{V_2}}{\overrightarrow{V_2}\cdot \overrightarrow{V_2}}$$    若矢量$V$仅采用$c_2\overrightarrow{V_2}$近似表示，则定义误差矢量$\overrightarrow{V_e}$，满足
$$\overrightarrow{V_e}=\overrightarrow{V}-c_2\overrightarrow{V_2}$$

1.1.2 n维空间的矢量正交分解

    从二维空间拓展至三维空间，甚至$n$维空间，对于任意矢量$V$，其皆可表示为n个正交矢量的线性组合，即
$$\overrightarrow{V}=c_1\overrightarrow{V_1}+c_2\overrightarrow{V_2}+\cdots +c_r\overrightarrow{V_r}+\cdots +c_n\overrightarrow{V_n}$$    其中，$\overrightarrow{V_i}\cdot \overrightarrow{V_j}=0,\left(i\ne j\right)$，第r个分量的系数为
$$c_r=\frac{\overrightarrow{V}\cdot \overrightarrow{V_r}}{\overrightarrow{V_r}\cdot \overrightarrow{V_r}}$$    类比二维空间矢量的近似表示，若$n$维空间的矢量同样以非完全正交基近似表示，即
$$\overrightarrow{V}\approx c_1\overrightarrow{V_1}+c_2\overrightarrow{V_2}+\cdots +c_r\overrightarrow{V_r}+\cdots +c_m\overrightarrow{V_m}，\left(m<n\right)$$同样存在一个误差矢量$\overrightarrow{V_e}$（划重点）。

1.2 信号的正交分解

    类似于矢量空间的正交分解，信号空间同样存在相似概念。对于某一一维信号，其可近似表示为$n$个正交函数${\phi }_1\left(t\right)$、${\phi }_2\left(t\right)$、…、${\phi }_n\left(t\right)$的线性组合，即
$$f\left(t\right)\approx c_1{\phi }_1\left(t\right)+c_2{\phi }_2\left(t\right)+\cdots +c_i{\phi }_i\left(t\right)+\cdots +c_n{\phi }_n\left(t\right)=\sum _{j=1}^n{c}_j{\phi }_j\left(t\right)$$其中，任意两个正交函数在区间$\left(t_1,t_2\right)$内满足
$${\int }_{t_1}^{t_2}{\phi }_i\left(t\right){\phi }_j^{\ast }\left(t\right)dt=\{\begin{array}{l}0,i\ne j\\ k,i=j\end{array}$$    此时均方误差$\overline{{\epsilon }^2}$满足
$$\overline{{\epsilon }^2}=\frac{{\int }_{t_1}^{t_2}{\left[f\left(t\right)-{\sum }_{j=1}^n{c}_j{\phi }_j\left(t\right)\right]}^{2}dt}{t_2-t_1}$$    为使得误差值最小，则$c_i$应满足
$$\frac{\partial \overline{{\epsilon }^2}}{\partial c_i}=0$$即
$$c_i=\frac{{\int }_{t_1}^{t_2}f\left(t\right){\phi }_i\left(t\right)dt}{{\int }_{t_1}^{t_2}{\phi }_i^2\left(t\right)dt}$$    当$n\to \infty$，即正交函数集为完备正交函数集时，误差为0。此时$f\left(t\right)$的广义傅里叶级数表示为
$$f\left(t\right)=\sum _{i=1}^{\infty }{c}_i{\phi }_i\left(t\right)$$

2. 周期信号的傅里叶级数

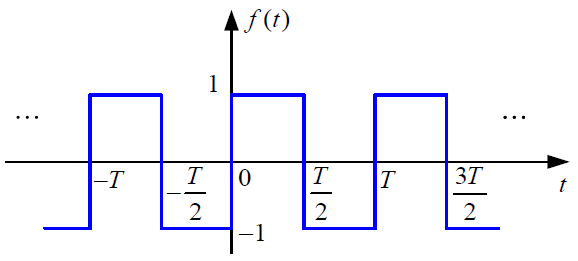
    周期函数（如下图所示）的傅里叶级数展开需满足Dirichlet条件：

• 在一个周期内，函数需连续或者拥有有限个数的第一类间断点（可去间断点、跳跃间断点）；
• 在一个周期内，函数拥有有限个数的极大值和极小值点；
• 在一个周期内，函数绝对可积。
  

2.1 三角形式的傅里叶级数

    当正交函数集为三角函数集 { 1 , cos ⁡ ( n Ω t ) , sin ⁡ ( n Ω t ) , n = 1 , 2 , 3 , ⋯   } left { 1,cos left ( nOmega t right ) ,sin left ( nOmega t right ),n=1,2,3,cdots right } {1,cos(nΩt),sin(nΩt),n=1,2,3,⋯}时，周期为$T\left(T=2\pi /\Omega \right)$的函数$f\left(t\right)$可以展开为三角形式的傅里叶级数
$$f\left(t\right)=\frac{a_0}{2}+\sum _{n=1}^{\infty }{a}_n\cos \left(n\Omega t\right)+\sum _{n=1}^{\infty }{b}_n\sin \left(n\Omega t\right)$$
其中
$$\frac{a_0}{2}=\frac{{\int }_{-\frac{T}{2}}^{\frac{T}{2}}1\cdot f\left(t\right)dt}{{\int }_{-\frac{T}{2}}^{\frac{T}{2}}{1}^{2}dt}=\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f\left(t\right)dt$$$$a_n=\frac{{\int }_{-\frac{T}{2}}^{\frac{T}{2}}\cos \left(n\Omega t\right)\cdot f\left(t\right)dt}{{\int }_{-\frac{T}{2}}^{\frac{T}{2}}{\cos }^2\left(n\Omega t\right)dt}=\frac{2}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}\cos \left(n\Omega t\right)f\left(t\right)dt$$$$b_n=\frac{{\int }_{-\frac{T}{2}}^{\frac{T}{2}}\sin \left(n\Omega t\right)\cdot f\left(t\right)dt}{{\int }_{-\frac{T}{2}}^{\frac{T}{2}}{\sin }^2\left(n\Omega t\right)dt}=\frac{2}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}\sin \left(n\Omega t\right)f\left(t\right)dt$$    当然，上式可以变换为余弦函数形式表示，即
$$f\left(t\right)=\frac{a_0}{2}+\sum _{n=1}^{\infty }{A}_n\cos \left(n\Omega t+{\phi }_n\right)$$其中，
$$A_n=\sqrt{a_n^2+b_n^2}$$$${\phi }_n=-\arctan \frac{b_n}{a_n}$$    这里$A_n$为偶函数，${\phi }_n$为奇函数，上式的物理意义在于，周期函数可以表示为直流分量和余弦分量的和，其中$\frac{a_0}{2}$表示直流分量，$A_1\cos \left(\Omega t+{\phi }_1\right)$表示基波分量（或一次谐波），$A_2\cos \left(2\Omega t+{\phi }_2\right)$表示二次谐波…，$A_n\cos \left(n\Omega t+{\phi }_n\right)$表示n次谐波。

2.2 指数形式的傅里叶级数

    当正交函数集为虚指数函数集$\left\{e^{jn\Omega t},n=0,\pm 1,\pm 2,\pm 3,\cdots \right\}$时，周期为$T\left(T=2\pi /\Omega \right)$的函数$f\left(t\right)$可以展开为指数形式的傅里叶级数，
$$\begin{array}{rl}f\left(t\right)& =\frac{A_0}{2}+\sum _{n=1}^{\infty }{A}_n\cos \left(n\Omega t+{\phi }_n\right)\\ & =\frac{A_0}{2}+\sum _{n=1}^{\infty }\frac{A_n}{2}\left(e^{j\left(n\Omega t+{\phi }_n\right)}+e^{-j\left(n\Omega t+{\phi }_n\right)}\right)\\ & =\frac{A_0}{2}+\sum _{n=1}^{\infty }\frac{A_n}{2}{e}^{j\left(n\Omega t+{\phi }_n\right)}+\sum _{n=1}^{\infty }\frac{A_n}{2}{e}^{-j\left(n\Omega t+{\phi }_n\right)}\\ & =\frac{A_0}{2}+\sum _{n=1}^{\infty }\frac{A_n}{2}{e}^{j\left(n\Omega t+{\phi }_n\right)}+\sum _{n=-1}^{-\infty }\frac{A_{-n}}{2}{e}^{-j\left(-n\Omega t+{\phi }_{-n}\right)}\\ & =\frac{A_0}{2}+\sum _{n=1}^{\infty }\frac{A_n}{2}{e}^{j\left(n\Omega t+{\phi }_n\right)}+\sum _{n=-1}^{-\infty }\frac{A_n}{2}{e}^{j\left(n\Omega t+{\phi }_n\right)}\\ & =\sum _{n=-\infty }^{\infty }\frac{A_n}{2}{e}^{j{\phi }_n}{e}^{jn\Omega t}\end{array}$$    令傅里叶系数为$F_n$，则
$$\begin{array}{rl}{F}_n& =\left|F_n\right|e^{j{\phi }_n}\\ & =\frac{1}{2}{A}_n{e}^{j{\phi }_n}\\ & =\frac{1}{2}\left(A_n\cos {\phi }_n+j{A}_n\sin {\phi }_n\right)\\ & =\frac{1}{2}\left(a_n-j{b}_n\right)\\ & =\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f\left(t\right)\cos \left(n\Omega t\right)dt-j\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f\left(t\right)\sin \left(n\Omega t\right)dt\\ & =\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f\left(t\right)e^{-jn\Omega t}dt\end{array}$$

2.3 周期信号的频谱

    日常生活中，我们习惯于在时域去表征信号，直观的去感受信号幅度随时间的变化。但其实时域分析并不足以全面反映信号中所蕴藏的信息。根据上述分析，既然信号可以分解为多个正交函数之和，每个函数又对应着不同的频率，那么信号本质上也可以在频域这一维度去表征，直观反映各个频率下，信号幅度和相位的分布情况。
    我们将周期信号分解后，各分量幅度随频率的变化称为幅度谱，各分量相位随频率的变化称为相位谱。而所谓的频谱图即将幅度和相位分量用一定高度的直线表示。
    上面几节我们得到了周期信号的三角形式和指数形式的傅里叶级数，如下所示
$$f\left(t\right)=\frac{a_0}{2}+\sum _{n=1}^{\infty }{A}_n\cos \left(n\Omega t+{\phi }_n\right)$$$$f\left(t\right)=\sum _{n=-\infty }^{\infty }\frac{A_n}{2}{e}^{j{\phi }_n}{e}^{jn\Omega t}=\sum _{n=-\infty }^{\infty }{F}_n{e}^{jn\Omega t}$$    根据上述两种傅里叶级数展开形式中n的取值范围不同，我们定义了单边谱和双边谱的概念，如下表所示。

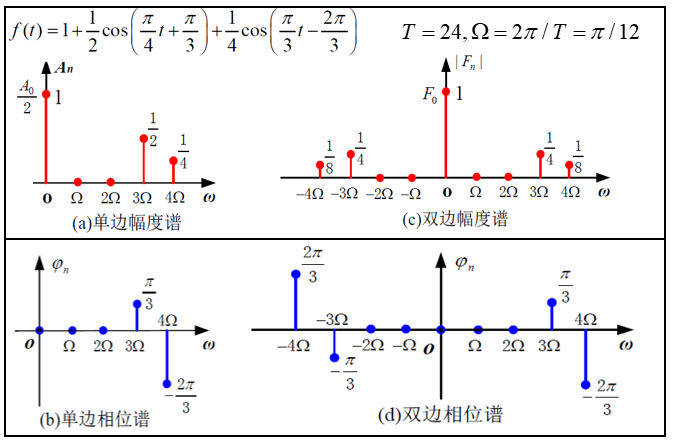
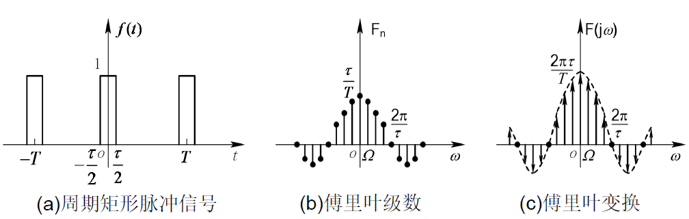
    $|F_n|$为偶函数，且双边幅度谱的直流分量的谱线高度与单边幅度谱相同，其余分量为单边谱的的一半，可以由单边幅度谱做关于$y$轴对称得到。${\phi }_n$为奇函数，双边相位谱可以由单边相位谱直接关于零点做中心对称得到。举个例子，周期函数$f\left(t\right)$的频谱图如下图所示。

3. 非周期信号的傅里叶变换

3.1 傅里叶变换的引入

    对于周期信号而言，其可以展开为傅里叶级数，那对于非周期信号呢？其是否也有类似的特点呢？下面我们继续从周期信号的频谱进行分析。对于常见的周期矩形脉冲函数，其周期为T，幅度为1，脉冲宽度为$\tau$，如下图所示。

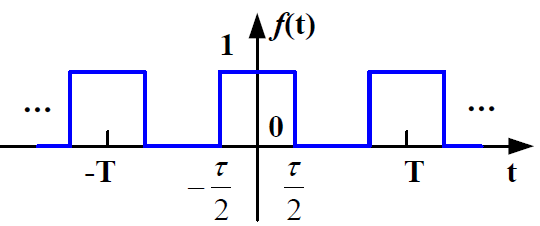
    对该函数的频谱进行求解，简略过程如下：
$$\begin{array}{rl}{F}_n& =\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f\left(t\right)e^{-jn\Omega t}dt\\ & =\frac{1}{T}{\int }_{-\frac{\tau }{2}}^{\frac{\tau }{2}}{e}^{-jn\Omega t}dt\\ & =\frac{\tau }{T}\frac{\sin \frac{n\Omega \tau }{2}}{\frac{n\Omega \tau }{2}}\\ & =\frac{\tau }{T}Sa\left(\frac{n\Omega \tau }{2}\right)\end{array}$$    其中，基频$\Omega =2\pi /T$，零点为$\frac{n\Omega \tau }{2}=m\pi \to n\Omega =\frac{2m\pi }{\tau }$，两零点间谱线间隔数为$\frac{2\pi }{\tau }/\frac{2\pi }{T}=\frac{T}{\tau }$，频谱图如下图所示。

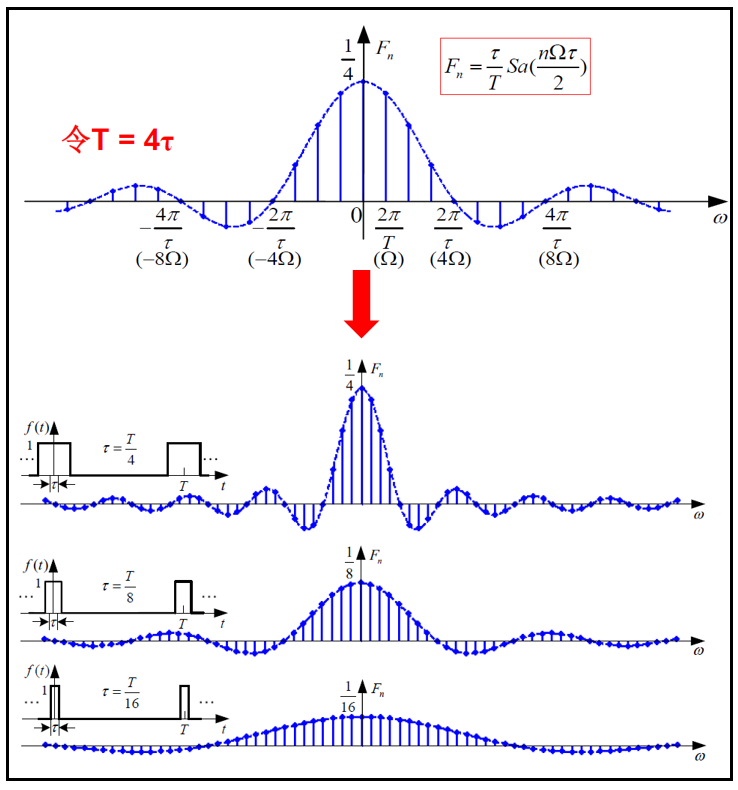
    从上图可以看出，周期信号的频谱是以基频$\Omega$为间隔的若干离散谱线组成的，谱线仅含有基频$\Omega$的整数倍分量，且随着频率的增加，幅度逐渐减小。同时，我们也可以得到如下推论：

1. 当$T$保持不变，$\tau$减小时，谱线的间隔$\Omega$不变，谱线的幅度减小，零点右移，两零点间的谱线数目$\frac{T}{\tau }$ 增加；
2. 当$\tau$保持不变，$T$增加时，谱线的间隔$\Omega$减小，谱线的幅度减小，零点位置不变，两零点间的谱线数目$\frac{T}{\tau }$ 增加。

    实际上，非周期信号即为周期无穷大的周期信号，此时，谱线间隔趋近于0，谱线幅度也趋近于0，信号的频谱将由离散谱过渡为连续谱,.但是在这一过程中，虽然各频率分量的幅度趋近于无穷小，但无穷小量之间仍有相对大小差别。为了放大这一差异性，我们引入频谱密度函数这一概念。
    我们已知周期信号的频谱函数如下：
$$F_n=\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f\left(t\right)e^{-jn\Omega t}dt$$    当$T\to \infty$时，$\Omega \to d\omega$，$n\Omega \to \omega$，
    则单位频率上的频谱为
$$\begin{array}{rl}F\left(j\omega \right)=\underset{T\to \infty }{\lim }\frac{F_n}{1/T}& =\underset{T\to \infty }{\lim }{F}_{n}T\\ & =\underset{T\to \infty }{\lim }{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f\left(t\right)e^{-jn\Omega t}dt\\ & ={\int }_{-\infty }^{\infty }f\left(t\right)e^{-j\omega t}dt\end{array}$$
    $F\left(j\omega \right)$称为$f\left(t\right)$的傅里叶变换，$f\left(t\right)$存在傅里叶变换的充分条件为$f\left(t\right)$绝对可积。

3.2 傅里叶逆变换

    根据傅里叶级数
$$f\left(t\right)=\sum _{n=-\infty }^{\infty }\frac{A_n}{2}{e}^{j{\phi }_n}{e}^{jn\Omega t}=\sum _{n=-\infty }^{\infty }{F}_n{e}^{jn\Omega t}=\sum _{n=-\infty }^{\infty }{F}_{n}T{e}^{jn\Omega t}\frac{1}{T}$$    当$T\to \infty$时，$\Omega \to d\omega$，$n\Omega \to \omega$，
$$\frac{1}{T}=\frac{\Omega }{2\pi }=\frac{d\omega }{2\pi }$$$$f\left(t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F\left(j\omega \right)e^{j\omega t}d\omega$$

4. 周期信号的傅里叶变换

    目前为止，对于周期信号，我们可以得到其傅里叶级数展开，并将对应的系数称为频谱（离散谱），对于非周期信号，我们可以对其进行傅里叶变换，同样对应的系数为信号的频谱（准确的说是频谱密度，连续谱），但二者并不相同，前者表示某一频率下，信号的幅度大小，后者表示单位频率下，信号的幅度大小。
    那对于周期信号和非周期信号，是否可以统一使用傅里叶变换进行分析？接下来将对该问题进行阐述。
    再搬出周期信号指数形式的傅里叶级数
$$f_T\left(t\right)=\sum _{n=-\infty }^{\infty }\frac{A_n}{2}{e}^{j{\phi }_n}{e}^{jn\Omega t}=\sum _{n=-\infty }^{\infty }{F}_n{e}^{jn\Omega t}$$
    傅里叶系数
$$F_n=\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f\left(t\right)e^{-jn\Omega t}dt$$
    对$f_T\left(t\right)$做傅里叶变换，
$$\begin{array}{rl}F\left[f_T\left(t\right)\right]& =F\left[\sum _{n=-\infty }^{\infty }{F}_n{e}^{jn\Omega t}\right]\\ & =\sum _{n=-\infty }^{\infty }{F}_{n}F\left[e^{jn\Omega t}\right]\\ & =\sum _{n=-\infty }^{\infty }{F}_{n}2\pi \delta \left(\omega -n\Omega \right)\\ & =2\pi \sum _{n=-\infty }^{\infty }{F}_n\delta \left(\omega -n\Omega \right)\end{array}$$
    由此可见，周期信号$f_T\left(t\right)$的频谱实际上是强度为$2\pi F_n$的冲激序列。其实也是在意料之中，因为频谱密度实质上是T倍的傅里叶级数系数，当T趋近无穷大时，离散谱各谐波分量处幅值变为无穷大，即演变为冲激函数。举个例子，如下图所示。

5. 写在最后

    看到现在只是对傅里叶变换有了些新的认识，郭老师的课对能量谱和功率谱简单的讲了一下，懂了又似乎没完全懂，感觉还需要补一下随机信号分析，待更。

最后

以上就是老迟到网络为你收集整理的信号与系统——傅里叶变换☞一维信号0. 引言1. 广义傅里叶级数2. 周期信号的傅里叶级数3. 非周期信号的傅里叶变换4. 周期信号的傅里叶变换5. 写在最后的全部内容，希望文章能够帮你解决信号与系统——傅里叶变换☞一维信号0. 引言1. 广义傅里叶级数2. 周期信号的傅里叶级数3. 非周期信号的傅里叶变换4. 周期信号的傅里叶变换5. 写在最后所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。