文章目录
- 什么是决策树
- 自己归纳一下
- 举个栗子
- 决策树模型构建
- 决策树的组成
- 流程
- 切分特征
- 信息熵
- 再举个栗子
- 信息增益ID3
- 决策树构造实例
- 一种特殊情况——信息增益率C4.5
- 另一种选定标准——CART和GINI系数
- 遇到连续值怎么搞?
- 决策树的剪枝
- 为什么要剪枝?
- 剪枝策略
- 代码部分
- 使用sklearn中的房价数据,判断经纬度对房价的影响。
- 可以看到一堆的参数:
- 可视化决策树
- 使用sklearn处理数据:
- 使用sklearn的GridSearchCV来选择最优的参数组合
什么是决策树
下面一大串是百科的描述(表示看不懂):
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干,故称决策树。在机器学习中,决策树是一个预测模型,他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度,使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。
决策树是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。
分类树(决策树)是一种十分常用的分类方法。他是一种监管学习,所谓监管学习就是给定一堆样本,每个样本都有一组属性和一个类别,这些类别是事先确定的,那么通过学习得到一个分类器,这个分类器能够对新出现的对象给出正确的分类。这样的机器学习就被称之为监督学习。
自己归纳一下
- 从根节点开始一步步走到叶子节点(决策),每个节点就是一个条件,根据不同的条件把数据进行区分。所有的数据最终都会落到叶子节点,既可以做分类也可以做回归
举个栗子
构建一个决策树分类器,用来区分是否喜欢打游戏。首先认为年龄<15岁的人群喜欢打游戏,接下来再以是否是男生为条件来区分一次,这样就得到分类结果。
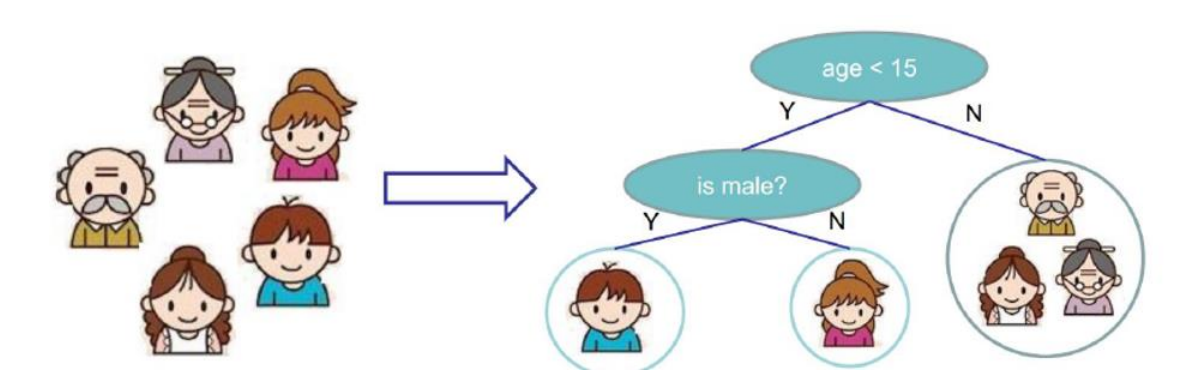
决策树模型构建
决策树的组成
- 根节点:第一个选择点
- 叶节点表示一个分类条件
- 非叶子节点与分支:中间过程
- 叶子节点:最终的决策结果
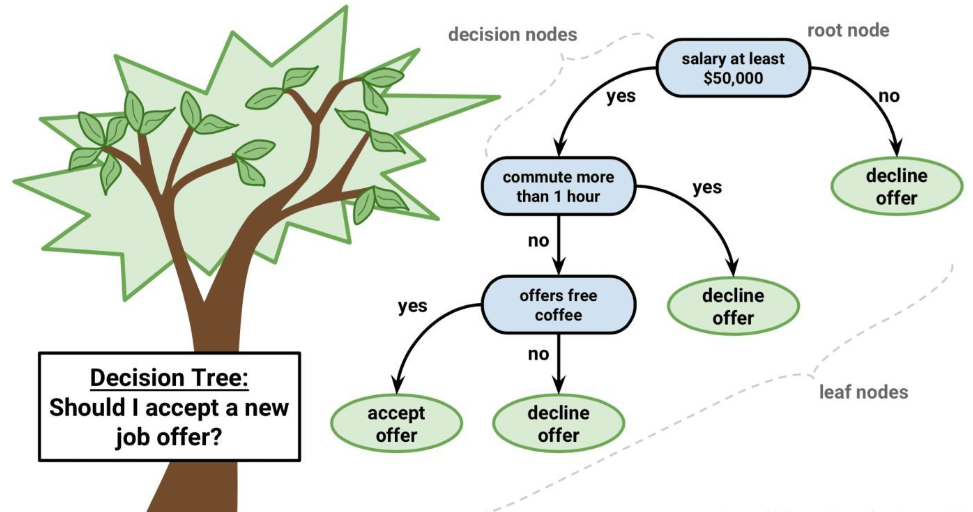
流程
- 训练阶段:给定一个数据集,选择某个条件作为根节点,随后再选择其他的调节作为叶节点去构建就可以了。
- 测试阶段:把测试数据丢进构件好的模型,等待输出结果。
一旦构建好了模型,分类或者预测任务就很简单了,只要把测试数据拿到模型里跑就行了。我们只要关注一个问题:如何构建一个决策树?围绕这个问题,再解决其他问题就行了。
切分特征
选择不同的条件作为根节点或者叶节点,对结果的影响肯定是很大的。特别是根节点的选择,显然比叶节点还要总要。
所以我们要通过一个指标来确定:到底用哪个条件作为优先选择的叶节点或者是根节点。这就引入了一个概念——信息熵。
信息熵
熵是表示随机变量不确定性的度量,熵值越高,表示混乱程度越高,越充满不确定性。
- 举个栗子:去杂牌店购物比去专卖店购物的熵值更高,因为杂牌店可能卖很多品牌的商品,你买到不同品牌的概率就很大,而去专卖店购物就只能买到一个品牌的商品。
熵 计 算 公 式 : H ( x ) = − ∑ P i ∗ L o g P i , i = 1 , 2... n 熵计算公式:H(x) = -sum P_i*LogP_i,i=1,2...n 熵计算公式:H(x)=−∑Pi∗LogPi,i=1,2...n
看下图的log函数图像(忽略文字,草稿而已···),i必定是一个概率值,所以值域就是[0,1],结合公式,概率越小,月不确定,在这个范围内的log图像就是log值越小,熵H(x)越大。
这就是为什么说,去专卖店购物买到一个品牌的商品概率为1(在log图像上就趋近0),它的熵就小的原因。

再举个栗子
A集合[1,1,1,1,1,1,1,1,2,2]
B集合[1,2,3,4,5,6,7,8,9,1]
显然A集合的熵值要低,因为A里面只有两种类别,相对稳定一些,而B中类别太多了,熵值就会大很多。
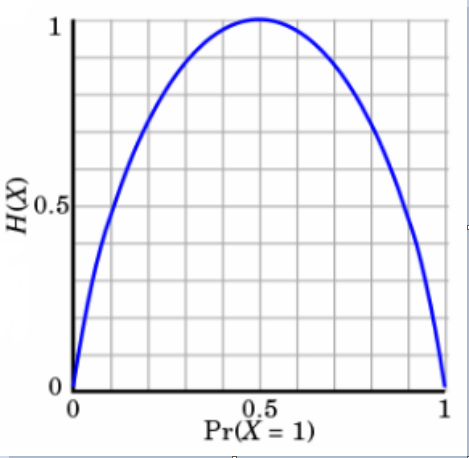
不确定性越大,得到的熵值也就越大
当p=0或p=1时,H§=0,随机变量完全没有不确定性
当p=0.5时,H§=1,此时随机变量的不确定性最大
所以熵是大的好还是小的好?为了解决这个问题又引入了一个概念:信息增益
信息增益ID3
信息增益的意思就是做一次决策后,使熵减小了,减小的程度就是信息增益。(分类后的专一性,希望分类后的结果是同类在一起)
一般来说,选择信息增益大的条件作为最初的根节点,其他的节点也是以信息增益为标准来衡量的,总之优先选择信息增益大的条件就ok了。
决策树构造实例
知道了信息增益大的条件优先选择后,来看一个著名的例子:
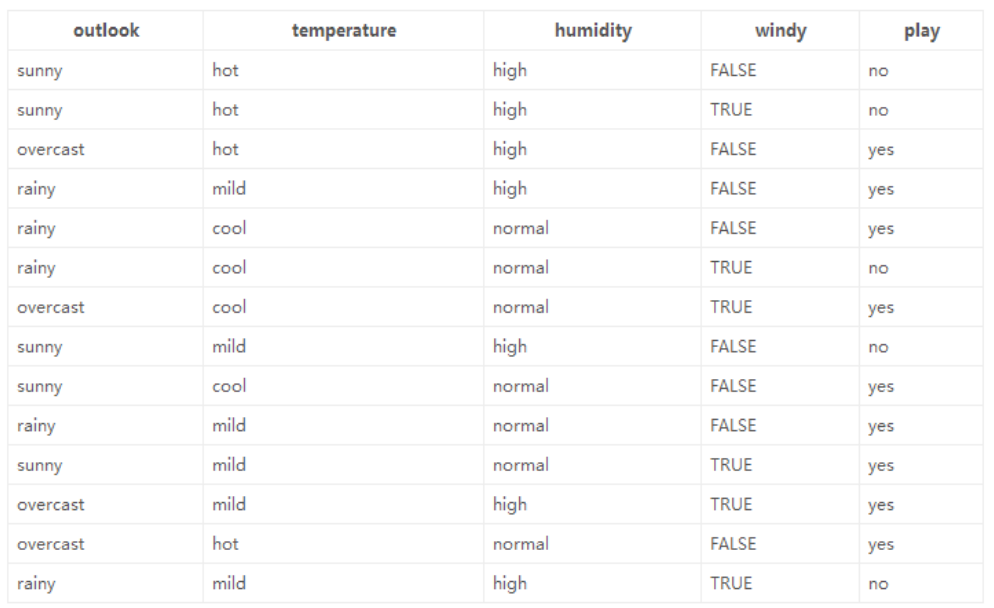
数据是14天内去不去打球的情况,特征包括天气情况、温度、湿度、是否有风。
-
先计算总的熵
在历史数据中(14天)有9天打球,5天不打球,所以此时的熵应为:
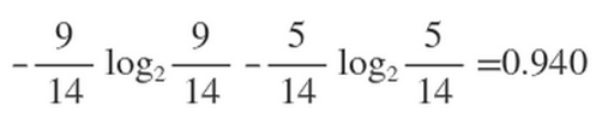
Outlook = sunny时,熵值为0.971
Outlook = overcast时,熵值为0
Outlook = rainy时,熵值为0.971 -
接下来分别计算四个条件的信息增益
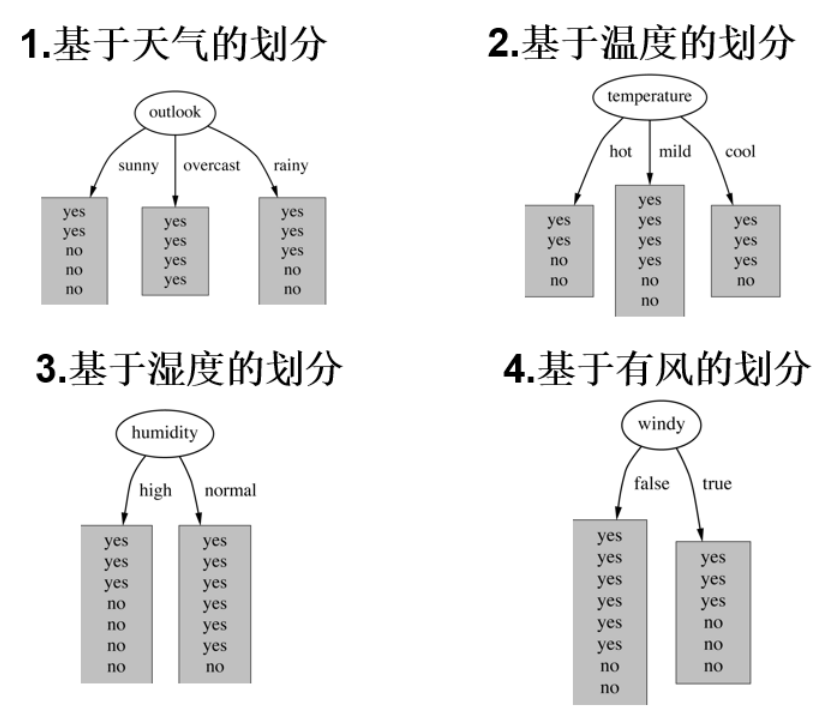
以outlook取值分别为sunny,overcast,rainy的概率为例:
熵值计算:5/14 * 0.971 + 4/14 * 0 + 5/14 * 0.971 = 0.693。
另外三个条件的信息增益分别为:0.029、0.152、0.048。
如果以天气为根节点,熵值从原始的0.940下降到了0.693,增益为0.247,我们只要按照信息增益的大小进行节点选择就ok了。
一种特殊情况——信息增益率C4.5
假如现在有一个条件,条件自身与最后的决策并无关联。但是他的条件属性值非常多,这个时候信息增益就很大,这时为了剔除信息增益的这种弊端,就引入了一个概念信息增益率。
计算这个条件本身的熵,肯定是一个非常大的值,因此对分类可能并没有什么帮助,所以就不去使用这个条件。
另一种选定标准——CART和GINI系数
CART的原理和熵的衡量标准是一样的,只是计算公式有所不同,CART使用GINI系数来衡量:
G I N I 系 数 公 式 : G I N I ( P ) = ∑ k = 1 n P k ( 1 − P k ) = 1 − ∑ k = 1 k P 2 k GINI系数公式:GINI(P) = sum_{k=1}^n P_k (1-P_k)=1-sum_{k=1}^kP^2k GINI系数公式:GINI(P)=k=1∑nPk(1−Pk)=1−k=1∑kP2k
遇到连续值怎么搞?
和sigmoid一样,找个分界点就好了···
比如:把成绩从低到高排序,以60分为界限判断是否及格。
决策树的剪枝
为什么要剪枝?
决策树过拟合风险很大,理论上可以完全分得开数据。想象一下,如果树足够庞大,每个叶子节点不就一个数据了嘛?这个时候拿测试集过来用,肯定是有问题的。所以需要剪枝处理。
剪枝:顾名思义,去除一些节点,可以提高算法的性能或者是效果。
剪枝策略
-
预剪枝:边建立决策树边进行剪枝的操作(更实用),预剪枝可以从限制深度,叶子节点个数
叶子节点样本数,信息增益量这些方面来设定是否需要剪掉某个节点。 -
后剪枝:当建立完决策树后来进行剪枝操作,不理会构建的过程。后剪枝的衡量公式:
C a ( T ) = C ( T ) + α ∗ ∣ T l e a f ∣ C_a (T)=C(T)+α*|T_{leaf}| Ca(T)=C(T)+α∗∣Tleaf∣
T代表的就是叶子节点的个数,因此,最后叶子节点越多,剪枝的数量就越多。
这些都是相对的,各种指标主要还是看阈值吧,所谓的调参,指的就是选择合适的阈值···
代码部分
使用sklearn中的房价数据,判断经纬度对房价的影响。
import matplotlib.pyplot as plt
import pandas as pd
# sklearn自带的房价预测数据集
from sklearn.datasets.california_housing import fetch_california_housing
housing = fetch_california_housing()
# print(housing)
housing.data.shape
# print(housing.data[0])
from sklearn import tree
# 创建一个回归树,max_depth指定树的深度
dtr = tree.DecisionTreeRegressor(max_depth=2)
# 传入数据和标签
dtr.fit(housing.data[:, [6, 7]],housing.target)
print(dtr)
打印结果:
DecisionTreeRegressor(criterion='mse', max_depth=2, max_features=None,
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best')
可以看到一堆的参数:
| 参数名 | 含义用法 |
|---|---|
| riterion | gini or entropy 选择用GINI系数或是熵进行决策 |
| splitter | best or random 前者是在所有特征中找最好的切分点 后者是在部分特征中(数据量大的时候),一般用best |
| max_features | None(所有),log2,sqrt,N 特征小于50的时候一般使用所有的 |
| max_depth | 树的最大深度。数据少或者特征少的时候可以不管这个值,如果模型样本量多,特征也多的情况下,可以尝试限制下 |
| min_samples_split | 如果某节点的样本数少于min_samples_split,则不会继续再尝试选择最优特征来进行划分如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。 |
| min_samples_leaf | 这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝,如果样本量不大,不需要管这个值,大些如10W可是尝试下5 |
| min_weight_fraction_leaf | 这个值限制了叶子节点所有样本权重和的最小值,如果小于这个值,则会和兄弟节点一起被剪枝默认是0,就是不考虑权重问题。一般来说,如果我们有较多样本有缺失值,或者分类树样本的分布类别偏差很大,就会引入样本权重,这时我们就要注意这个值了。 |
| max_leaf_nodes | 通过限制最大叶子节点数,可以防止过拟合,默认是"None”,即不限制最大的叶子节点数。如果加了限制,算法会建立在最大叶子节点数内最优的决策树。如果特征不多,可以不考虑这个值,但是如果特征分成多的话,可以加以限制具体的值可以通过交叉验证得到。 |
| class_weight | 指定样本各类别的的权重,主要是为了防止训练集某些类别的样本过多导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重如果使用“balanced”,则算法会自己计算权重,样本量少的类别所对应的样本权重会高。 |
| min_impurity_split | 这个值限制了决策树的增长,如果某节点的不纯度(基尼系数,信息增益,均方差,绝对差)小于这个阈值则该节点不再生成子节点。即为叶子节点 。 |
| n_estimators | 单个决策树不需要用到。要建立树的个数 |
先大概记录一下,有需要用到再去深究····
可视化决策树
需要安装相关的依赖和框架,点这里查看具体依赖
# pydotplus使决策树可视化
# 需要安装相关控件
import pydotplus
graph = pydotplus.graph_from_dot_data(dot_data)
graph.get_nodes()[7].set_fillcolor("#FFF2DD")
graph.write_pdf("tree_test_result.pdf")
运行完后会在项目根目录出现一个pdf文件:
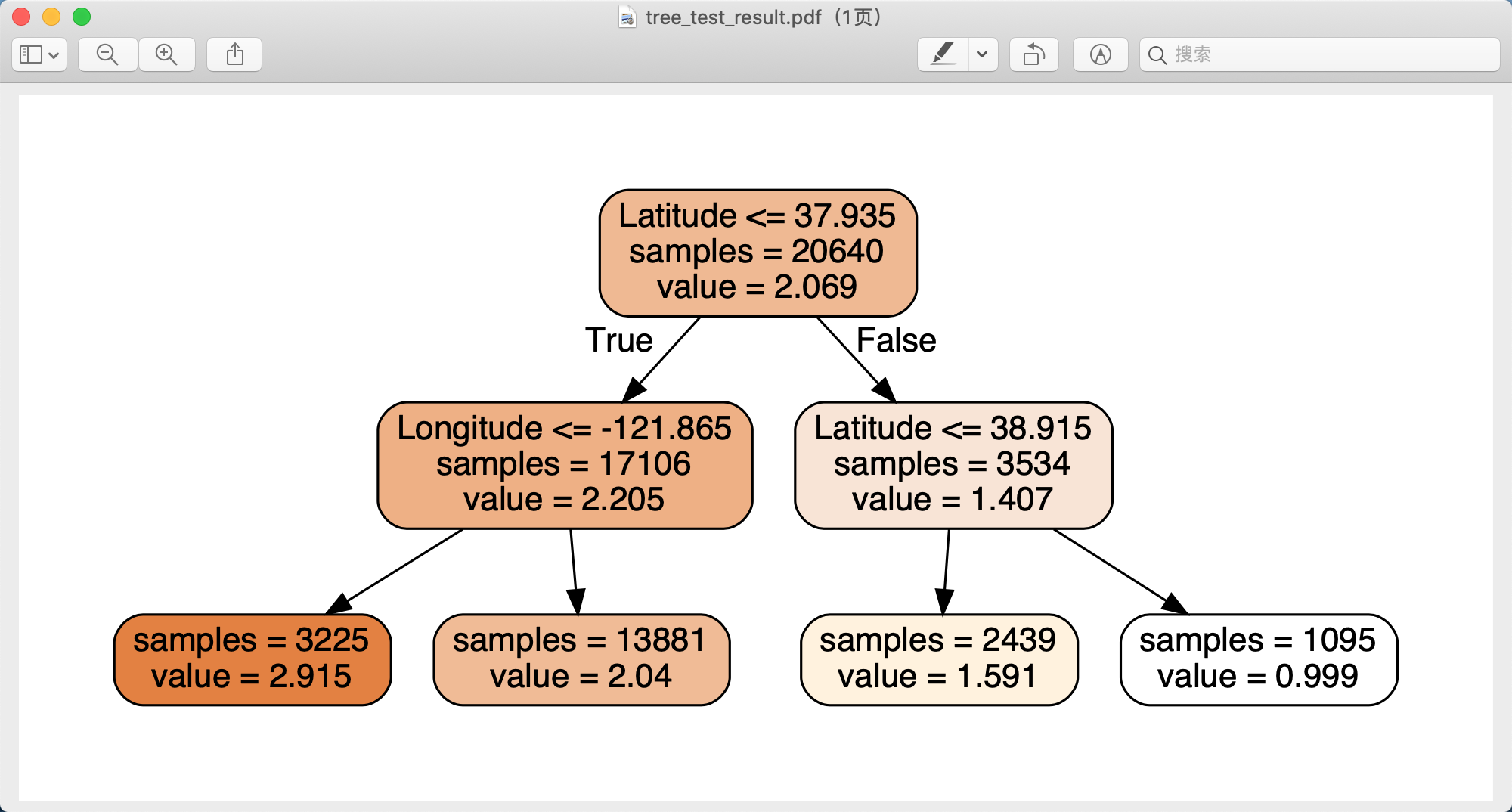
使用sklearn处理数据:
# 导入sklearn的数据切割
from sklearn.model_selection import train_test_split
# 将数据集分为测试集和验证集 test_size=0.1 取10%为测试集
data_train, data_test, target_train, target_test = train_test_split(housing.data, housing.target, test_size=0.1,
random_state=42)
# 决策树回归器。
dtr = tree.DecisionTreeRegressor(random_state=42)
# 从训练集(x,y)建立一个决策树回归器。
dtr.fit(data_train, target_train)
# 测试 不同的算法 score函数需要的数据是不一样的,根据情况而定,可以查官方文档
dtr.score(data_test, target_test)
random_state:随机数种子
使用sklearn的GridSearchCV来选择最优的参数组合
GridSearchCV可以指定一个数据集,里面以字典的形式,传入一些参数集合,让框架自行得出最优的集合。这个函数在其他算法中也常用到,可以熟练掌握。
# 选择参数
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeRegressor
# 构建参数候选项的字典 只指定两个参数 相当于有3*3=9次结果
tree_params = {'max_depth': list((2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 100))}
# 传入算法类型+参数列表+交叉验证次数
grid = GridSearchCV(DecisionTreeRegressor(), param_grid=tree_params, cv=5)
# 训练
grid.fit(data_train, target_train)
# print(grid.grid_scores)
print(grid.best_params_)
print(grid.best_score_)
输出结果:
{'max_depth': 9}
0.6920626557441106
意思就是当树的深度是9的时候 能够得到最优的参数组合。
最后
以上就是危机衬衫最近收集整理的关于决策树算法的总结归纳什么是决策树决策树模型构建代码部分的全部内容,更多相关决策树算法内容请搜索靠谱客的其他文章。








发表评论 取消回复