仅以此文纪念过往的岁月
一.总结
决策树 ,顾名思义是一种决策类型的树,回想一下树的结构,存在层次和节点,其中每一个非叶节点均是一种决策类型,每一个叶子均是一种决策结果。但是其缺点存在过拟合的现象。
二.决策树简介
决策树比较符合人类的思考模式,如下示例
实例:
简单例子如下:
一个老妈向女儿推荐了一个相亲对象,一般女孩子会问一些问题,通过这些问题来判断是否去见,
女儿:多大了
老妈:26
女儿决策:大于30不见,太老了,小于25不见,太小了
女儿:有房没?
老妈:有
女儿决策:有房不错,可以,没房不见,穷屌丝
女儿:收入高不?
老妈:一般,是个公务员
女儿决策:可以见见
如果将上面的对话表示成树的结构,如下图所示:
上面的图的数据再量化后,则就是一个决策树
决策树的官方定义
决策树(decisiontree)是一个树结构(可以是二叉树或非二叉树)。其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果
三.决策树的构造
决策树的构造的核心在于策略的选择,即选择某一个特征,根据属性的不同构造不同的分支,其目标是分裂子集尽量“纯”。
属性选择有多种判定基准ID3,C4.5算法等。
分裂属性时,分三种情况:
1. 树结构不要求为二叉树时,每一个属性划分均为一个分支
2. 树结构要求为二叉树时,使用属性划分的子集,区分属于子集,不属于子集,分为两个分支
3. 数值为连续值,取分裂点,小于该值为一个分支,大于等于该值为一个分支。
ID3算法
设D为用类别对训练元组进行的划分,则D的熵(entropy)表示为:
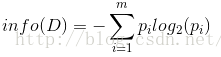
其中pi表示第i个类别在整个训练元组中出现的概率,可以用属于此类别元素的数量除以训练元组元素总数量作为估计。熵的实际意义表示是D中元组的类标号所需要的平均信息量。
现在我们假设将训练元组D按属性A进行划分,则A对D划分的期望信息为:
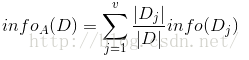
而信息增益即为两者的差值:
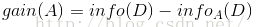
以下面示例简单说明上面的公式
| ID
| 日志密度 | 好友密度 | 是否使用真实头像 | 账号是否真实 |
| 1 | S | s | n | n |
| 2 | s | l | y | y |
| 3 | l | m | y | y |
| 4 | m | m | y | y |
| 5 | l | m | y | y |
| 6 | m | l | n | y |
| 7 | m | s | n | n |
| 8 | l | m | n | y |
| 9 | m | s | n | y |
| 10 | s | s | y | n |
目标是根据日志密度,好友密度,是否使用真实头像来区分账号是否真实
计算熵值,样本量10,假账号3,真实账号7
Ptrue = 7/10 = 0.7
Pfalse = 3/10 =0.3
Info(D) =-0.3log(0.3)-0.7log(0.7) = 0.876
计算日志密度熵值,日志密度分为3类S,L,M
其中L分类,样本总数10,L类3,L类中假账号0 真实账号3
Info(L) =0.3*(-0/3*log(0/3)-3/3*log(3/3))
其中S分类,样本总数10,L类3,L类中假账号2 真实账号1
Info(S) =0.3*(-2/3*log(2/3)-1/3*log(1/3))
其中M分类,样本总数10,L类4,L类中假账号1 真实账号3
Info(M) = 0.4*(-1/4*log(1/4)-3/4*log(3/4))
Infol(D) = Info(L)+Info(S)+ Info(M) = 0.603
所以gain(L) = 0.876-0.603 = 0.273
同理可以计算出好友密度和是否使用真实头像的信息增益为0.553和0.033
因为好友密度为最大信息增益,所以使用好友密度该特征作为分裂节点。
根据上述分裂,继续递归分裂,得到决策树。
ID3.5 偏向于使用多值属性,如果存在唯一标识属性ID,则ID3会选择它作为分裂属性,这样虽然使得划分充分纯净,但这种划分对分类几乎毫无用处。
例如表格中唯一ID
Info(D) =-1/10*(-0/1log(0/1)-1/1log(1/1)) = 0;
其gain为0.876,ID3算法会使用唯一ID作为分裂属性,但是对于分类几乎毫无用处。
C4.5算法
ID3的后继算法C4.5使用增益率(gain ratio)的信息增益扩充,试图克服这个偏倚。
C4.5算法首先定义了“分裂信息”,其定义可以表示成:
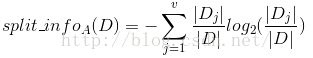
其中各符号意义与ID3算法相同,然后,增益率被定义为:
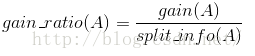
根据上述示例中, 日志密度的分裂信息如下
Split_info =-0.3log(0.3)- 0.3log(0.3)- -0.4log(0.4) = 1.571
则日志密度的增益率为
Gain_ratio (D) =0.273/1.571 = 0.174
唯一ID的增益率为
Split_Info =-1/10log(1/10)*10 = 2.302
Gain_ratio =0.876/2.302 = 0.381
感觉C4.5依然会采用唯一ID作为分裂属性,其原因为样本量少,如果样本量很巨大,其Splite_info会趋向无穷大,则gain_ratio趋向无穷小,则不会选择唯一ID作为分裂属性。
四. 剪枝
为什么需要剪枝,因为决策树趋向完美的对训练集进行分类,但是训练集包含了无数种可能,世界上没有一种完美的模型能够处理一种事情,所有成功的模型都是不完美的,因为不完美,才能包容一切。人也是一样。
训练数据集中如果存在噪声或离群点,如果没有剪枝,决策树也会将这些干扰完美的分类,但是噪声或离群点其实是没什么用的数据,反而导致决策树的异常。对于训练集看起来时完美的,但是对于测试集则效果底下。
所以为了不完美,就需要将决策树剪枝,剪枝分两种
1. 预剪枝
1.1 限制树生长的深度,缺点:需要事先设置,如果不清楚模型所需的树的深度,如果过于限制树深度,则模型趋于一般,无法准确分类。如果设置的树深度过大,则失去了剪枝的意义
1.2 限制样本最小值,如果划分后的子集小于设置的最小值,则停止树的生长,该节点变为叶子节点。此时如果出现子集不纯的现象,voting来抉择。
2. 后剪枝
剪枝之后,对该节点的类别判别是用“大多数原则“,选择当前数据集下的最多的类标签为该节点的类别。
1)Reduced Error Pruning:误差降低剪枝
最简单粗暴的一种后剪枝方法,其目的减少误差样本数量。 采用测试集数据来做判定。
f
(
T
)
=
−
∑
t∈T
e
(
t
)
其中
e(t
)表示在节点
t
下的样本的误判个数;
T
表示当前树的节点。
f
(
T
′
)
=
−
∑
t∈
T
′
e
(
t
)
其中
T
表示去掉某个节点
N
之后的树的节点;
e(t
)表示某个节点下的训练样本点误判数量。
剪枝的条件:
f
(
T)⩽f(T′),即
e(
t
K′)⩽e(tK)
剪枝之后使得误差降低。
说明:上述是理论的说明,其实就是测试集去测试所有节点。比较暴力,耗时较长。
2)Pessimistic Error Pruning:悲观错误剪枝
该方法基于训练数据的误差评估,因此不用单独找剪枝数据集。但训练数据也带来错分误差偏向于训练集,因此需要加入修正1/2。是自上而下的修剪。
具有
T
个节点的树的误差率衡量为:
E
(
T)=∑t∈Te(t)+1/2N(t)
去掉节点
K
之后
T
个节点的树的误差衡量为(此衡量方法侧重对每个节点的衡量),有的在前面加负号的,基本推导是一致的,剪枝条件的结论是一样的。
E
(
T′)=∑t∈T,excepKe(t)+1/2N(t)
e(t
)表示节点
t
之下的训练集的误判的个数。
N
(
t)表示节点
t
之下的训练集的总个数。
设
n(t
)=e(t)+1/2N(t)
可以证明
E
(
T′)−E(T)=n(t′K)−n(tK)=e(tK′)−e(tK)N(t)
即:带着某个点的该支的误判个数-去掉某点之后该支的误判个数 再除以该支的总个数。
剪枝的条件是:
SE(n(tK′))=n(tK′)∗(N(t)−n(tK′))N(t)−−−−−−−−−−−−−−√⩽E(T′)−E(T)=e(tK′)−e(tK)N(t)
3)Minimum Error Pruning:最小误差剪枝[1]
该方法由Niblett&Bratko1987年发明。与悲观错误剪枝方法相近,但是对类的计数处理是不同的。自底向上剪枝。
初始版本是:
Epruning
=n−nc+k−1n+k
E
表示在某节点剪枝之后的一个期望误差率,
n
表示该节点的样本数量,
n
表示其中类别最多的样本个数,
k
表示数据的标签类别个数。此处有个假设:所有样本是均等的。
Enotpruning
=∑Msplit=1|Ssplit||S|∗Esplit−pruning
其中
|
表示分裂为某一支的样本比例
剪枝的条件:
Epruning
⩽Enotpruning则剪掉该节点。
改进版本是: [1][2]
一个观测样本到达节点
t
,其隶属于类别
i
的概率为:
pi
(t)=ni(t)+paimN(t)+m
其中,
ni
(t)表示该节点下的训练样本中,被判断为
i
类的样本数量。
pai
表示在该类别的先验概率。
N
(
t)表示该节点下训练样本的数量。
m
是评估方法的一个参数(m可以依据数据噪声给出,但是也可以作为一个参数,调节一下找到一个较合适的)。
对m-probability-estimates, the static error :
Es
在某一个节点的计算方式如下:
Es
=1−nc+pαcmN+m=N−nc+(1−pαc)mN+m
其中,
N
是节点所在支的样本数量;
nc
是该节点下类别最多的样本数量。
pαc
表示最多类别的先验概率。
若是不剪枝,则期望误差:
Esplit−s
=∑Msplit=1|Ssplit||S|∗Esplit−s
剪枝的条件:
Es
⩽Esplit−s则去掉该节点。
4)Cost-Complexity Pruning:代价复杂剪枝[3][4][5]
该方法在Breiman1984年的经典CART中首次提到并使用。
一棵树的好坏用如下式子衡量:
Rα
(T)=R(T)+αC(T)
其中
R(T
)表示该树误差(代价)的衡量;
C
(
T)表示对树的大小的衡量(可以用树的终端节点个数代表)。
α
表示两者的平衡系数,其值越大,树越小,反之树越大。
怎么用这个准则剪枝呢?
1.找到完整树的一些子树{
Ti
,i=1,2,3,...,m}。
2.分别计算他们的
Rα
(Ti),选择最小的
Rα
(Ti)所代表的树。
误差(代价)用训练样本,但最好十折计算。
5)Error-Based Pruning:基于错误的剪枝[6]
该方法由Quinlan在1992年的C4.5算法中首次提出并使用。使用测试集来剪枝。
对每个节点,计算剪枝前和剪枝后的误判个数,若是剪枝有利于减少误判(包括相等的情况),则减掉该节点所在分支。
6)Critical Value Pruning:
该方法由Mingers1987年发明。
树的生成过程中,会得到选择属性及分裂值的评估值,设定一个阈值,所有小于此阈值的节点都剪掉
四.决策树补充
1.属性用完了
属性用完了,但是子集还不是纯净集,怎么办,投票啊,少数服从多数,采用多数的类别作为此节点的类别,然后将此节点作为叶子节点。
本文是对决策树的总结,参考部分博文,如有侵权,请联系我。
最后
以上就是糊涂月光最近收集整理的关于决策树--总结的全部内容,更多相关决策树--总结内容请搜索靠谱客的其他文章。








发表评论 取消回复