机器学习--决策树（公式结论）

84 阅读 0 评论 56 点赞

我是靠谱客的博主糟糕煎饼，最近开发中收集的这篇文章主要介绍机器学习--决策树（公式结论），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

本文记录周志华《机器学习》决策树内容：***(文中公式内容均来自周志华《机器学习》)***

决策树是基于树结构进行决策问题的算法，一般来说，一棵决策树包括一个根节点、若干内部节点和若干个叶子节点(决策结果)，其余每个节点则对应于一个属性测试。每个节点包含的样本集合根据属性测试的结果被划分到子节点中。从而实现以下的类似结构
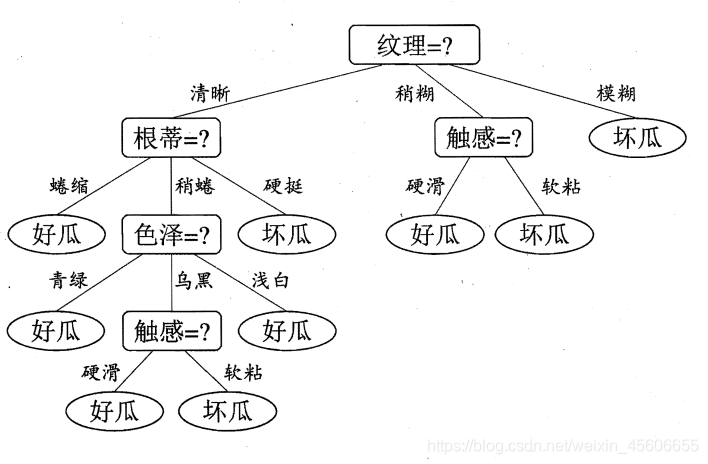
在这里插入图片描述
基础知识：

信息熵：度量样本集合纯度常用的指标，值越小，则D的纯度越高， ${p_k}$ 为样本集合D中第k类样本所占的比例 $(k = 1, 2, . . ., ∣ y ∣)$ 。
$sumlimits_{k = 1}^{|y|} {{p_k}{{log }_2}{p_k}}$
信息增益：考虑不同分支节点的样本数不同，故对其赋予权重 ${D^v}|/|D|$ ，即样本数越多的分支节点影响越大，式中a为离散属性，有V个可能的取值。信息增益越大越好。
$sumlimits_{v = 1}^V {{{|{D^v}|} over {|D|}}Ent({D^v})}$
增益率：信息增益准则对可取值数码较多的属性有所偏好，而增益率准则对可取值数目较少的属性有所偏好，因此C4.5算法不是直接选择增益率最大的候选划分属性，而是先从候选划分属性中宣传信息增益高于平均水平的属性，再在其中选择增益率最高的。 $Gain_ratio(D,a) = {{Gain(D,a)} over {IV(a)}}$ $sumlimits_{v = 1}^V {{{|{D^v}|} over {|D|}}{{log }_2}{{|{D^v}|} over {|D|}}}$
基尼指数(Gini):反映从数据集D中随机抽取两个样本，其类别标记不一致的概率。Gini(D)越小，则数据纯度越高。 $sumlimits_{k = 1}^{|y|} {{p_k}^2}$ 属性a的基尼指数，使得划分后基尼指数最小的属性为最优划分属性 $Gini_index(D,a) = sumlimits_{v = 1}^V {{{|{D^v}|} over {|D|}}Gini({D^v})}$

预防过拟合问题：【可以通过设立验证集，对比各个节点划分前后的精度，来缺定该节点是否需要划分】
5. 预剪枝：边建立决策树边进行剪枝操作(限制深度，叶子节点个数，叶子节点样本数，信息增益量等)
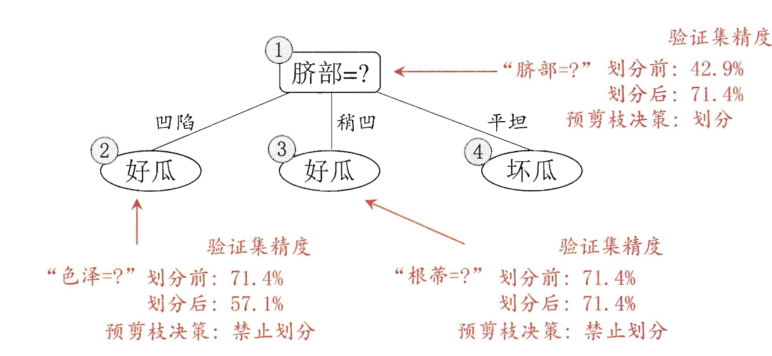
在这里插入图片描述
6. 后剪枝：建立完决策树后进行剪枝操作(通过一定的衡量标准）
后剪枝前：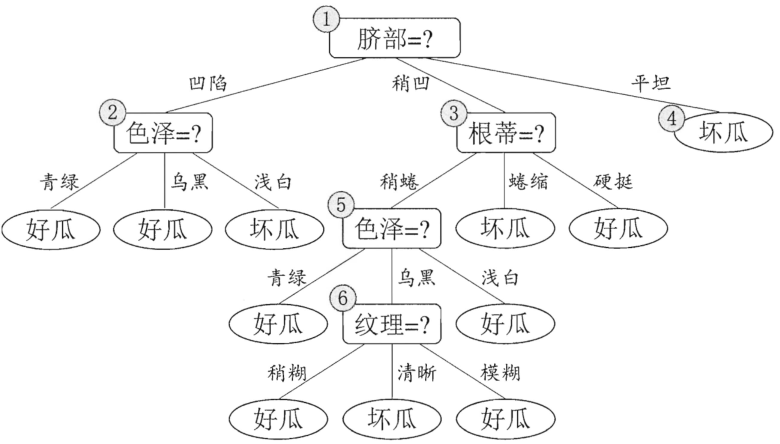
后剪枝后：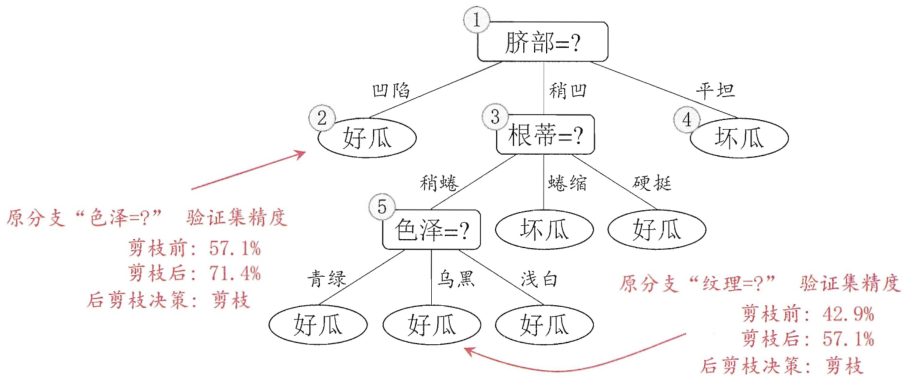
后剪枝决策树通常比预剪枝决策树保留了更多分支，故欠拟合风险很小，泛化性能往往由于预剪枝决策树，但其训练时间开销比未剪枝决策树和预剪枝决策树都要大很多。

连续属性处理：
当连续属性的可取值数目不再有限，因此不能直接根据连续属性的可取值来对节点进行划分，因此可利用连续属性离散化，如最简单的二分法对其进行处理。即将连续属性由小到大进行排序{a1,a2,…,an}，基于划分点t将D分为子集 $D_t^ -$ 和 $D_t^ +$ ，前者为再属性a上不大于t的样本，后者为大于t的样本，而划分点t的取值为 ${T_a} = { {{{a^i} + {a^{i + 1}}} over 2}|1 le i le n - 1}$
然后依次选取划分点，进行划分，从而计算信息增益，按照max(信息增益)的原则，选取最优划分点即可。
注意：与离散属性不同，若当前节点划分属性为连续属性，该属性还可作为其后代节点的划分属性。

算法流程：（利用递归操作）
在这里插入图片描述
大致流程：
1.判断是否递归返回：当前节点包含样本全部属于同一类别；当前属性集为空，或所有样本在所有属性上取值相同无法划分。符合以上两种情况，则返回类别值的众数。
2.遍历属性，计算分割后的信息增益，选取最优分割属性
3.如果最优分割属性为离散属性，则剔除。以后不再使用其进行划分
4.按照最优分割属性，分割数据集，然后重新进行第一步，进行递归操作。

程序：

import operator
from math import log


def dataset():
    data = [[0, 0, 0.56, 0.8, 'no'],
               [0, 0, 0.34, 1.2, 'no'],
               [0, 1, 0.25, 1.8, 'yes'],
               [0, 1, 1.4, 0.3, 'yes'],
               [0, 0, 0.43, 0.5, 'no'],
               [1, 0, 0.24, 0.9, 'no'],
               [1, 0, 0.22, 1.9, 'no'],
               [1, 1, 1.14, 1.4, 'yes'],
               [1, 0, 1.87, 2.2, 'yes'],
               [1, 0, 1.44, 2.55, 'yes'],
               [2, 0, 1.0, 2.79, 'yes'],
               [2, 0, 1.55, 1.1, 'yes'],
               [2, 1, 0.14, 1.0, 'yes'],
               [2, 1, 0.58, 2.66, 'yes'],
               [2, 0, 0.44, 0.55, 'no']]
    lebels = ['F1', 'F2', 'F3', 'F4']
    return data, lebels


def creattree(data, labels, featlabels):
    classlist = [example[-1] for example in data]  # 当前数据的分类
    # 停止条件1---分类全部一致
    if classlist.count(classlist[0]) == len(classlist):
        return classlist[0]
    # 停止条件2---无可分属性
    if len(data[0]) == 1:
        return majorityCnt(classlist)

    bestfeat, threshold = chooseBestFeature(data)  # 选择最优分割属性id和连续属性时的分割阈值
    bestfeatlabel = labels[bestfeat]  # 最优分割属性
    information = (bestfeatlabel, threshold)
    featlabels.append(information)

    tree = {information: {}}

    if threshold == None:  # 离散属性
        del labels[bestfeat]  # 剔除此属性标签
        featvalue = [example[bestfeat] for example in data]
        uniqueVals = set(featvalue)  # 属性下不同值
        # 根据不同值创造多个子节点
        for value in uniqueVals:
            sublabels = labels[:]
            tree[information][value] = creattree(splitDisDataSet(data, bestfeat, value), sublabels, featlabels)  # 子节点
        return tree
    else:  # 连续属性
        uniquePolar = [0, 1]
        for polar in uniquePolar:
            sublabels = labels[:]
            tree[information][polar] = creattree(splitConDataSet(data, bestfeat, threshold, polar), sublabels, featlabels)  # 子节点
        return tree


# 返回类别数最多的类别id
def majorityCnt(classlist):
    classcount = {}
    for vote in classlist:
        if vote not in classcount.keys():
            classcount[vote] = 0
        classcount[vote] += 1
    sortedclasscount = sorted(classcount.items(), key=operator.itemgetter(1), reverse=True)
    return sortedclasscount[0][0]


def chooseBestFeature(data):
    numfeatures = len(data[0]) - 1  # 当前数据属性数量
    baseentropy = calnonent(data)  # 父节点熵值
    bestinfogain = 0
    bestfeature = -1
    threshold = None

    for i in range(numfeatures):
        featlist = [example[i] for example in data]
        uniquevals = set(featlist)  # 同一属性下不同值
        newentropy = 0  # 子节点熵值

        if type(featlist[0]) == int:
            for val in uniquevals:
                subdata = splitDisDataSet(data, i, val)  # 分割后的数据集(剔除当前属性)
                prob = len(subdata) / float(len(data))
                newentropy += prob * calnonent(subdata)
            infogain = baseentropy - newentropy  # 信息增益
            if infogain >= bestinfogain:
                bestinfogain = infogain
                bestfeature = i
                threshold = None

        if type(featlist[0]) == float:
            thresholds = sorted(uniquevals)
            entropy = baseentropy
            # 二分法
            for j in range(len(thresholds) - 1):
                thresholdlter = (thresholds[j] + thresholds[j+1]) / 2
                subdata_l = splitConDataSet(data, i, thresholdlter, 0)  # 负样本
                prob_l = len(subdata_l) / float(len(data))
                subdata_r = splitConDataSet(data, i, thresholdlter, 1)  # 正样本
                prob_r = len(subdata_r) / float(len(data))
                newentropy = prob_l * calnonent(subdata_l) + prob_r * calnonent(subdata_r)
                infogain = baseentropy - newentropy
                if infogain >= bestinfogain:
                    bestinfogain = infogain
                    bestfeature = i
                    threshold = thresholdlter
    return bestfeature, threshold


# 分割离散属性数据
def splitDisDataSet(data, axis, val):
    retdata = []
    for featvec in data:
        if featvec[axis] == val:
            reducedfeatvec = featvec[:axis]
            reducedfeatvec.extend(featvec[axis+1:])
            retdata.append(reducedfeatvec)
    return retdata


# 分割连续属性数据
def splitConDataSet(data, axis, threshold, polar):
    retdata = []
    for featvec in data:
        if polar == 0:
            if featvec[axis] <= threshold:
                reducedfeatvec = featvec[:axis]
                reducedfeatvec.extend(featvec[axis + 1:])
                retdata.append(reducedfeatvec)
        else:
            if featvec[axis] > threshold:
                reducedfeatvec = featvec[:axis]
                reducedfeatvec.extend(featvec[axis + 1:])
                retdata.append(reducedfeatvec)
    return retdata


def calnonent(dataset):
    numexamples = len(dataset)  # 数据个数
    labelCounts = {}
    # 计算各个标签值数量
    for featVec in dataset:
        currentlabel = featVec[-1]
        if currentlabel not in labelCounts.keys():
            labelCounts[currentlabel] = 0
        labelCounts[currentlabel] += 1
    shannonEnt = 0  # 当前节点熵值
    for key in labelCounts:
        prop = float(labelCounts[key]) / numexamples
        shannonEnt -= prop * log(prop, 2)
    return shannonEnt


if __name__ == '__main__':
    dataSet, labels = dataset()
    featLabels = []
    myTree = creattree(dataSet, labels, featLabels)
    print(myTree)