机器学习-决策树总结

决策树：LR模型是把所有特征塞入学习，而决策树类似if-else一样，去做条件判断。

信息熵越低，纯度越高。

信息熵计算：

信息增益：划分前的信息熵  -  划分后的信息熵。表示的是向纯度方向迈出的“步长”。

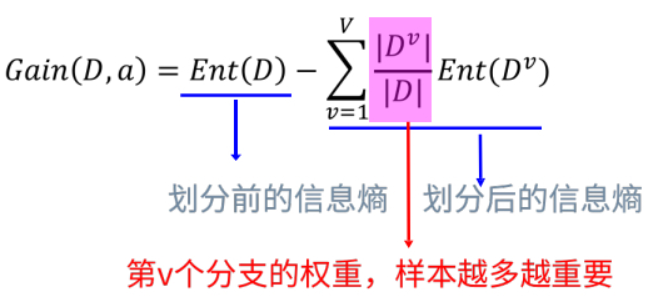
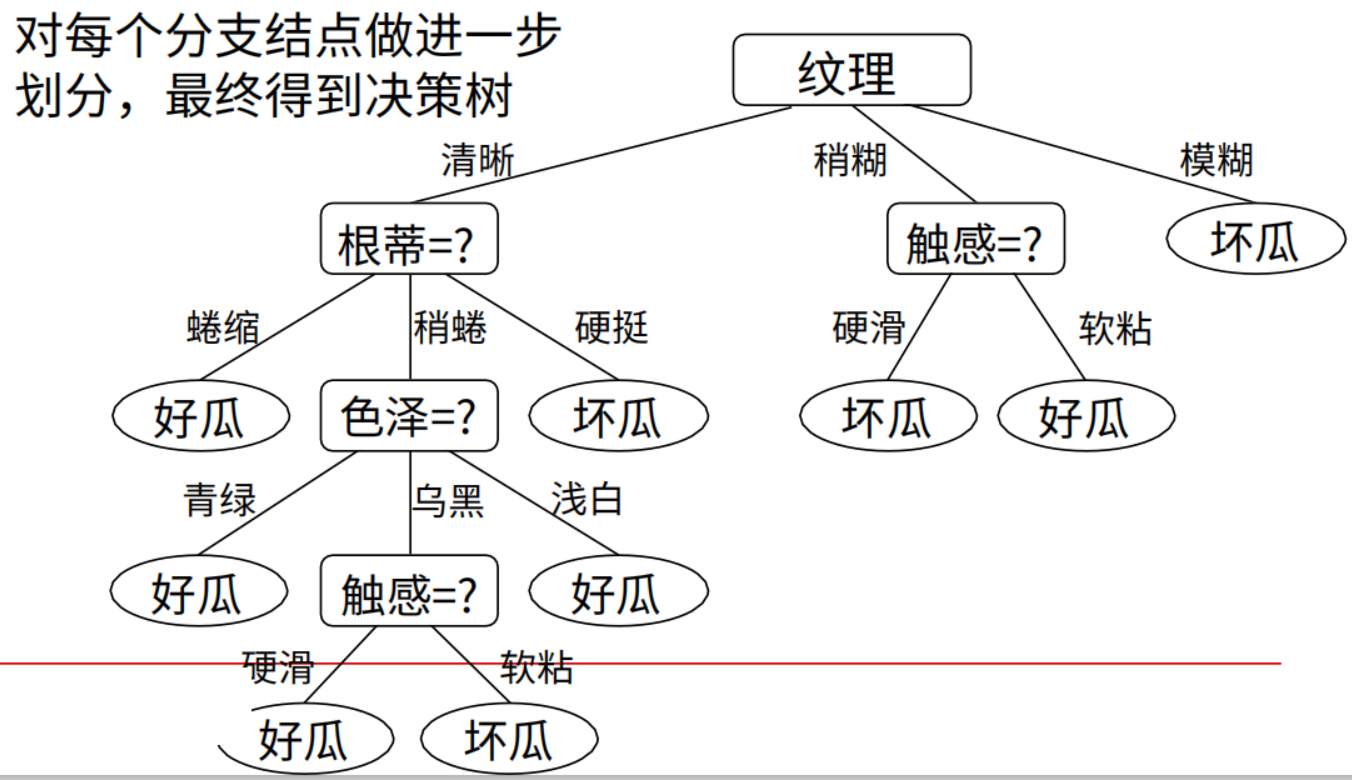
ID3：在根节点处计算信息熵，根据属性依次划分并计算其节点的信息熵，信息增益降序排列，排在前面的就是第一个划分属性，其后依次类推，这就得到了决策树的形状。

信息增益有一个问题：对可取值数目较多的属性有所偏好，例如：考虑将“编号”作为一个属性。

C4.5：使用信息增益率，

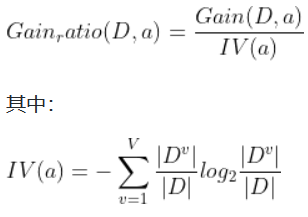
某属性的可能取值数目越多(即V越大)，则IV(a)的值通常就越大。

信息增益比本质是在信息增益的基础之上乘上一个惩罚参数。特征个数较多时，惩罚参数较小；特征个数较少时，惩罚参数较大。

缺点：信息增益率偏向取值较少的特征。

基于以上缺点，不是直接选择信息增益率最大的特征，而是在特征中找出信息增益高于平均水平的特征，然后在这些特征中再选择信息增益率最高的特征。

CART算法：使用基尼系数计算纯度

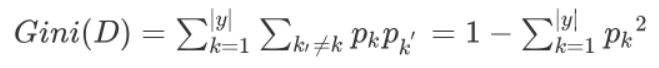
表示在样本集合中一个随机选中的样本被分错的概率。

举例来说，现在一个袋子里有3种颜色的球若干个，伸手进去掏出2个球，颜色不一样的概率。

Gini(D)越小，数据集D的纯度越高。

举个例子

假设现在有特征 “学历”，此特征有三个特征取值： “本科”，“硕士”， “博士”，

当使用“学历”这个特征对样本集合D进行划分时，划分值分别有三个，因而有三种划分的可能集合，划分后的子集如下：

1.划分点： “本科”，划分后的子集合 ： {本科}，{硕士，博士}

2.划分点： “硕士”，划分后的子集合 ： {硕士}，{本科，博士}

3.划分点： “博士”，划分后的子集合 ： {博士}，{本科，硕士}}

对于上述的每一种划分，都可以计算出基于 划分特征= 某个特征值 将样本集合D划分为两个子集的纯度：

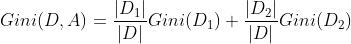
因而对于一个具有多个取值（超过2个）的特征，需要计算以每一个取值作为划分点，对样本D划分之后子集的纯度Gini(D,Ai)，(其中Ai 表示特征A的可能取值)

然后从所有的可能划分的Gini(D,Ai)中找出Gini指数最小的划分，划分的划分点便是使特征A对样本集合D划分的最佳划分点。

决策树不需要归一化：

数值缩放不影响分裂点位置，对树模型的结构不造成影响。 按照特征值进行排序的，排序的顺序不变，那么所属的分支以及分裂点就不会不同。

树模型是不能进行梯度下降的，因为构建树模型（回归树）寻找最优点时是通过寻找最优分裂点完成的，因此树模型是阶跃的，阶跃点是不可导的，并且求导没意义，也就不需要归一化。

既然树形结构（如决策树、RF）不需要归一化。

那为何非树形结构比如Adaboost、SVM、LR、Knn、KMeans之类则需要归一化。

对于线性模型，特征值差别很大时，运用梯度下降的时候，损失等高线是椭圆形，需要进行多次迭代才能到达最优点。

如果进行了归一化，等高线就是圆形，促使SGD往原点迭代，从而导致需要的迭代次数较少。

决策树的剪枝策略有 预剪枝 (Pre-Pruning) 和 后剪枝 (Post-Pruning)。

• 预剪枝：核心思想，在每一次实际对结点进行进一步划分之前，先采用验证集的数据来验证如果划分是否能提高划分的准确性。如果不能，就把结点标记为叶结点并退出进一步划分；如果可以就继续递归生成节点。
• 后剪枝：后剪枝则是先从训练集生成一颗完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来泛化性能提升，则将该子树替换为叶结点。

参考：

https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.Desition%20Tree/Desition%20Tree.md

最后

以上就是激昂台灯为你收集整理的机器学习-决策树总结的全部内容，希望文章能够帮你解决机器学习-决策树总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。