文章目录
- 1 三维空间中的位置与姿态
- 1.1 位置描述
- 1.2 姿态描述
- 2 相关函数详细用法
- 2.1 获取旋转矩阵 rot
- 2.2 绘制坐标系 trplot
- 2.3 动画演示 tranimate
关注微信公众号`二进制人工智能`,回复`robot`获取机器人工具箱
1 三维空间中的位置与姿态
通常来说,机器人指的是至少包含有一个固定刚体和一个活动刚体的机器装置。其中,固定的刚体称为基座,而活动的刚体称为末端执行器。在两个部件之间会有若干连杆和关
节来支撑末端执行器﹐并使其移动到一定的位置。
控制一个机器人的运动,可以通过控制机器人(机械臂)上各关节的位置,设定关节运动的轨迹。而首先需要做的就是获取机器人本身的位姿。所谓位姿,就是指机器人上每个关节在每一时刻的位置和姿态。这就需要确定描述空间物体位姿的方法,本书中使用空间坐
标系来描述相关位姿。当得到位姿的描述以后﹐就可以利用各关节位姿之间的关系来描述机器人的整个运动链,进而得到机器人的基座坐标系和末端执行器坐标系之间的关系。
机器人的运动学模型包括机器人各连杆、关节的位置姿态以及在各关节上的坐标系,其任务之一就是确立机器人末端执行器的位姿。机器人的机械臂通常是由一组关节连接的连杆结合体:第一个连杆固定﹐连接该机械臂的基座,而最后一个连杆连接的是它的末端执行器。操作机器人是为了控制与机器人相关的零件、工具在三维空间中运动,因此需要描述相应的位置和姿态。任务之一就是确立机器人末端执行器的位姿。机器人的机械臂通常是由一组关节连接的连杆结合体:第一个连杆固定﹐连接该机械臂的基座,而最后一个连杆连接的是它的末端执行器。操作机器人是为了控制与机器人相关的零件、工具在三维空间中运动,因此需要描述相应的位置和姿态。
1.1 位置描述
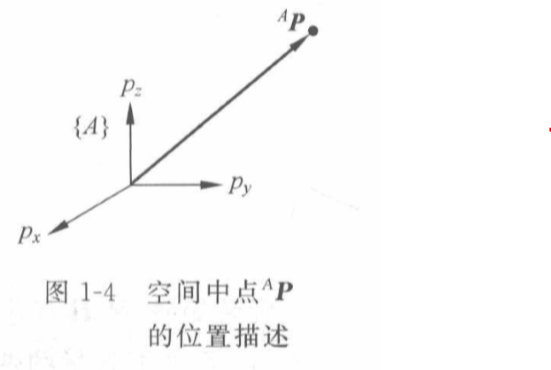
如图1-4所示,在三维空间中建立某一坐标系,于是空间中的任何一个点就可以通过一个
3
×
1
3×1
3×1的位置矢量来确定。建立一个直角坐标系
A
{A}
A,空间中的任一点
A
P
^AP
AP可以表示为:
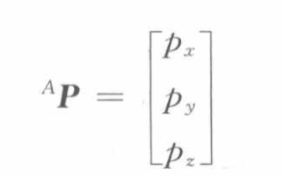
p x 、 p y 、 p z p_x、p_y、p_z px、py、pz分别是 A P ^AP AP在坐标系 A {A} A中的三个坐标分量, A P ^AP AP称为位置矢量。
1.2 姿态描述
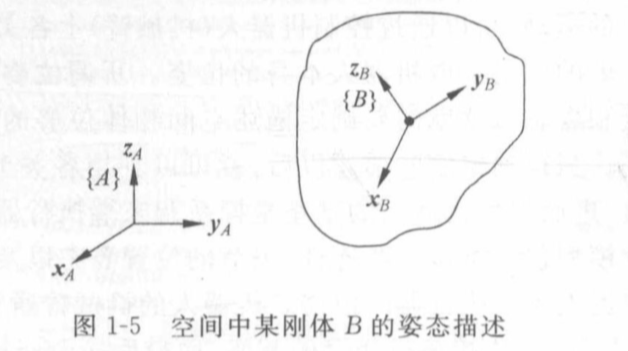
空间中的物体还需要描述它的姿态(也称为方位),这用固定在物体上的坐标系
B
{B}
B来描述。如图1-5所示,为了规定空间某刚体
B
B
B的方位,设一坐标系
B
{B}
B与此刚体固连﹔用三个单位矢量
x
B
,
y
B
,
z
B
x_B,y_B ,z_B
xB,yB,zB来表示坐标系
{
B
}
{B}
{B}的主轴方向﹐因此物体相对于参考坐标系
{
A
}
{A}
{A}的姿态可以用矢量
x
B
,
y
B
,
x
B
x_B ,y_B,x_B
xB,yB,xB相对于参考坐标系
A
{A}
A的方向余弦组成的
3
×
3
3×3
3×3矩阵来表示,这个矩阵
B
A
R
^A_BR
BAR称为旋转矩阵。
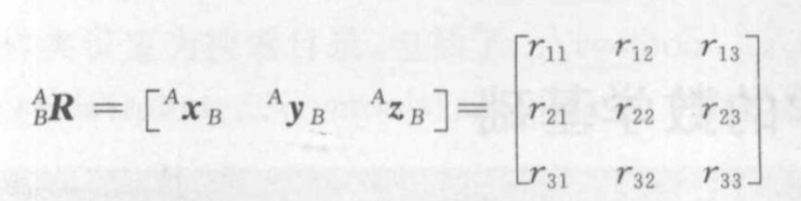
用矢量两两之间的余弦则表示为:
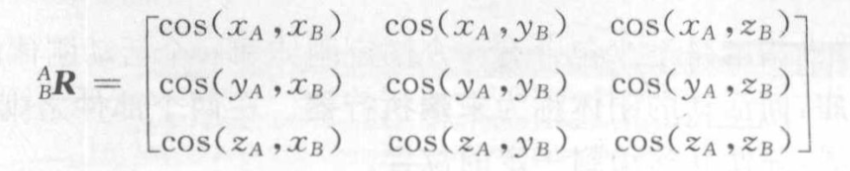
对应于轴
X
,
Y
X,Y
X,Y或
Z
Z
Z作转角为
θ
theta
θ的旋转变换,其旋转矩阵分别为:
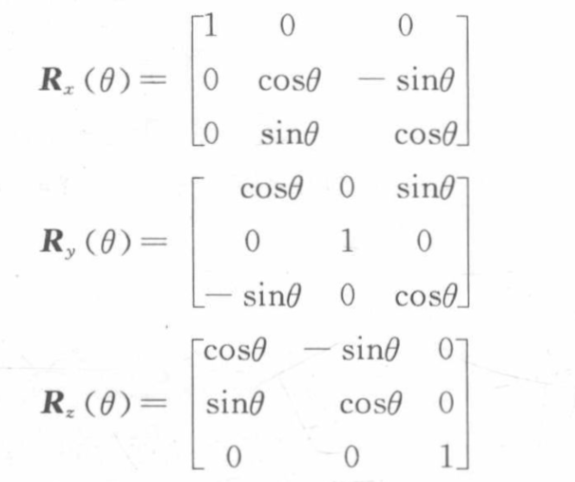
旋转矩阵
B
A
R
^A_BR
BAR具有这样的特点:
(1)3个主矢量两两垂直
(2)9个元素中,只有3个是独立的
(3)3个单位主矢量满足6个约束条件:
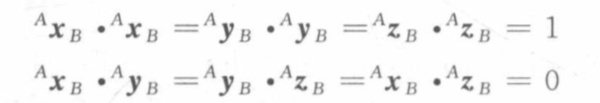
(4)旋转矩阵为正交矩阵,且满足条件:
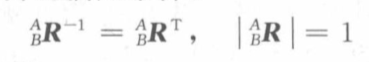
机器人工具箱中,可分别用函数
r
o
t
x
(
θ
)
,
r
o
t
y
(
θ
)
,
r
o
t
z
(
θ
)
rotx(theta),roty(theta),rotz(theta)
rotx(θ),roty(θ),rotz(θ)计算旋转
θ
theta
θ的旋转矩阵,并且在默认情况下,
θ
theta
θ用弧度表示。
例如围绕 X X X轴做转角为180°的旋转变换:
R=rotx(pi)
运行结果:
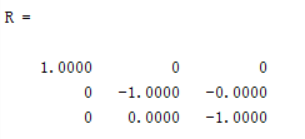
如果直接用角度
θ
theta
θ表示,可以分别用
r
o
t
x
(
θ
,
′
d
e
g
′
)
,
r
o
t
y
(
θ
,
′
d
e
g
′
)
,
r
o
t
z
(
θ
,
′
d
e
g
′
)
rotx(theta,'deg'),roty(theta,'deg'),rotz(theta,'deg')
rotx(θ,′deg′),roty(θ,′deg′),rotz(θ,′deg′)计算旋转矩阵:
R=rotx(180,'deg')
运行结果:

以上两种方式,都可以得到相对应的旋转矩阵。
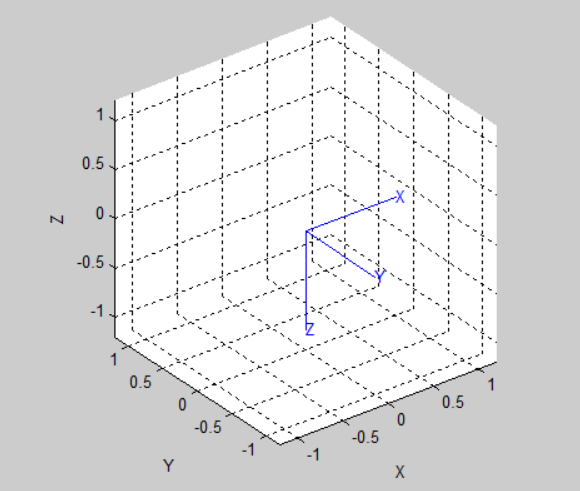
在机器人工具中,可以使用两种函数实现坐标的旋转可视化。函数trplot()可以用图形表示相应的体坐标系,函数tranimate用动画展示世界坐标系旋转为体坐标系的过程。
trplot(R)
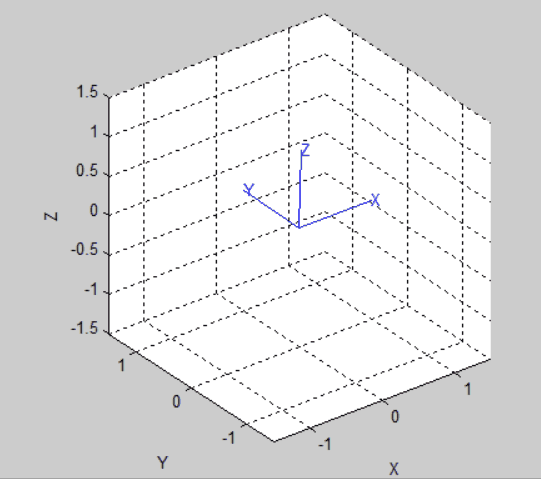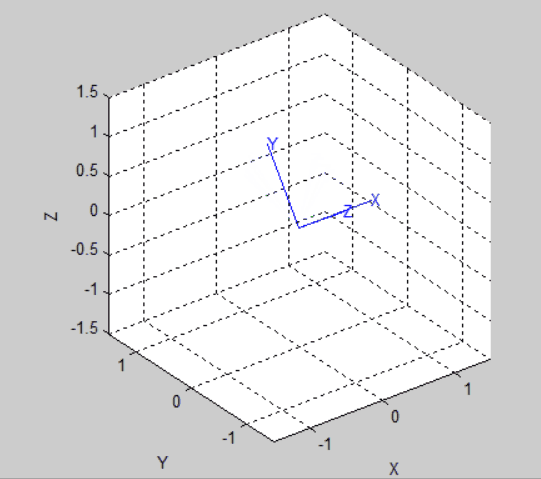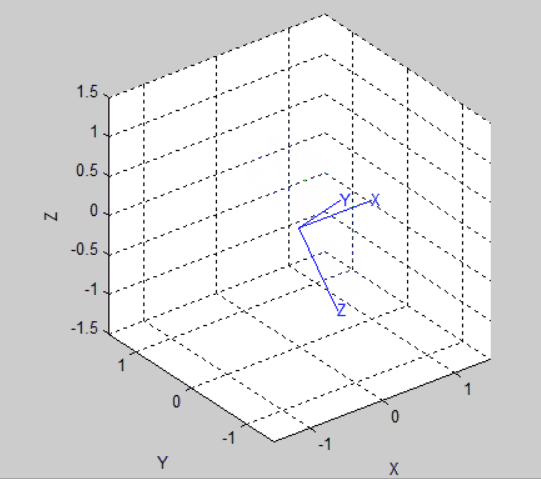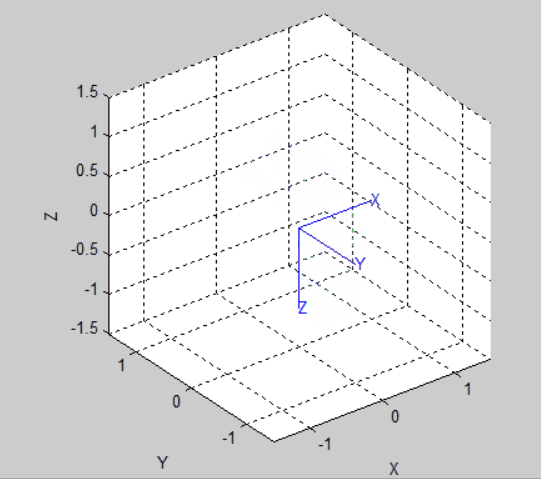
tranimate(R)
2 相关函数详细用法
2.1 获取旋转矩阵 rot
(1) rotx():R=rotx(
θ
theta
θ)是表示围绕X轴旋转弧度为
θ
theta
θ得到的旋转矩阵,返回一个3×3的矩阵R。
(2) roty():R=roty(
θ
theta
θ)是表示围绕Y轴旋转弧度为
θ
theta
θ得到的旋转矩阵,返回一个3×3的矩阵R。
(3) rotz():R=rotz(
θ
theta
θ)是表示围绕Z轴旋转弧度为
θ
theta
θ得到的旋转矩阵,返回一个3×3的矩阵R。
2.2 绘制坐标系 trplot
函数为:trplot()
对于三维坐标系的绘制,机器人工具箱提供了强大的可视化函数trplot()。
(1) trplot(R):绘制由旋转矩阵得到的坐标系,其中坐标系根据正交旋转矩阵围绕原点旋转得到,
R
R
R为3×3的矩阵。
(2) trplot(T):绘制由齐次变换矩阵T表示的三维坐标系,其中
T
T
T为4×4的矩阵。
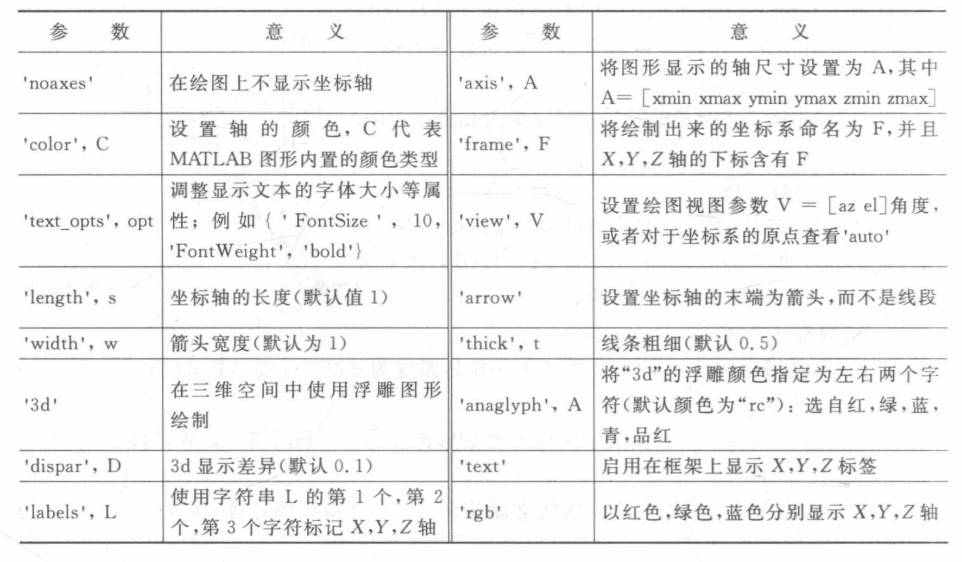
此外,它包含了许多可选参数,这里列举主要的几种:
2.3 动画演示 tranimate
函数为:tranimate()。
(1)tranimate( xl, x2,options)展示3D坐标系从姿态xl变换到姿态x2的动画效果。
其中,姿态xl和x2有三种表示方法:一个4×4的齐次矩阵,或一个3×3的旋转矩阵,或一个四元数。
(2) tranimate(x,options)展示了坐标系由上一个姿态变换到姿态x的动画效果。同样地,姿势x也有三种表示方法:一个4×4的齐次矩阵,或一个3×3的旋转矩阵,或一个四元数。
(3) tranimate(xseq,options)展示了移动一段轨迹的动画效果。xseq可以是一组
4
×
4
×
N
4×4×N
4×4×N的齐次矩阵,或一组
3
×
3
×
N
3×3×N
3×3×N的旋转矩阵,或是一组四元数向量(
N
×
1
N×1
N×1)。
它包含的可选参数如下:

《机器人仿真与编程技术》 杨辰光 李智军 许扬
最后
以上就是粗暴衬衫最近收集整理的关于【Robotics toolbox】(一)获取旋转矩阵 rot|绘制坐标系 trplot|动画演示 tranimate1 三维空间中的位置与姿态2 相关函数详细用法的全部内容,更多相关【Robotics内容请搜索靠谱客的其他文章。








发表评论 取消回复