微分方程是动态系统建模的基础。本文介绍了微分方程的解析解法。
我们在高等数学中已经学过，常系数线性微分方程是有解析解的。
常系数线性微分方程一般数学表示形式为：
我们可以把微分方程理解为一个动态的系统，其中，u是输入信号，y是输出信号，我们最用要求的是y的解析解。
dsolve函数：
y=dsolve(‘eqn1’,‘eqn2’,…,‘cond1’,‘cond2’,…,‘var’)
eqni表示方程，condi表示初值，var表示微分方程中的自变量，系统默认为t。
D为微分符号，D2表示二阶微分，D3表示三阶微分。
例题1：
1
2
3
4
5syms t y; %声明关键字 u=exp(-5*t)*cos(2*t+1)+5; uu=5*diff(u,t,2)+4*diff(u,t)+2*u; y=dsolve(['D4y+10*D3y+35*D2y+50*Dy+24*y=',char(uu)]) % D4y 表示y的四阶导数
点击查看diff函数的用法
执行代码，得到微分方程的解析解：
1
2
3
4y = (exp(-5*t)*(445*cos(2*t + 1) - 65*exp(5*t) + 102*sin(2*t + 1)))/26 - (exp(-5*t)*(537*cos(2*t + 1) - 40*exp(5*t) + 15*sin(2*t + 1)))/24 - (exp(-5*t)*(25*exp(5*t) - 542*cos(2*t + 1) + 164*sin(2*t + 1)))/60 - exp(-t)*((133*exp(-4*t)*cos(2*t + 1))/30 - (5*exp(t))/3 + (97*exp(-4*t)*sin(2*t + 1))/60) + C1*exp(-4*t) + C2*exp(-3*t) + C3*exp(-2*t) + C4*exp(-t)
在此题的解析解中，有c1, c2, c3, c4等几个量，这些常数称为待定系数，这样得到的解，就是原始问题的通解。
通解的检验：
将这个截带入到原始方程中去检验。
1
2
3
4
5
6
7
8syms t y; %声明关键字 u=exp(-5*t)*cos(2*t+1)+5; uu=5*diff(u,t,2)+4*diff(u,t)+2*u; y=dsolve(['D4y+10*D3y+35*D2y+50*Dy+24*y=',char(uu)]) % D4y 表示y的四阶导数 % 通解与检验 diff(y,4)+10*diff(y,3)+35*diff(y,2)+50*diff(y)+24*y-uu simplify(ans)
得到的结果：
1
2
3
4ans = 0
误差为0，得到的是原始方程的通解。
若已知微分方程的初值条件，则可得出微分方程的唯一解：
例如：
1
2
3
4
5
6
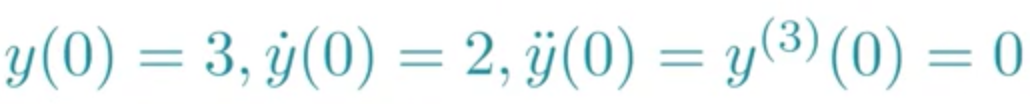
7syms t y; %声明关键字 u=exp(-5*t)*cos(2*t+1)+5; uu=5*diff(u,t,2)+4*diff(u,t)+2*u; y=dsolve(['D4y+10*D3y+35*D2y+50*Dy+24*y=',char(uu)],... 'y(0)=3','Dy(0)=2','D2y(0)=0','D3y(0)=0') ezplot(y,[0,5]) %ezplot（）：将微分方程的解用曲线绘制出来
同时，我们可以调用ezplot函数将微分方程的解用曲线的形式绘制出来。
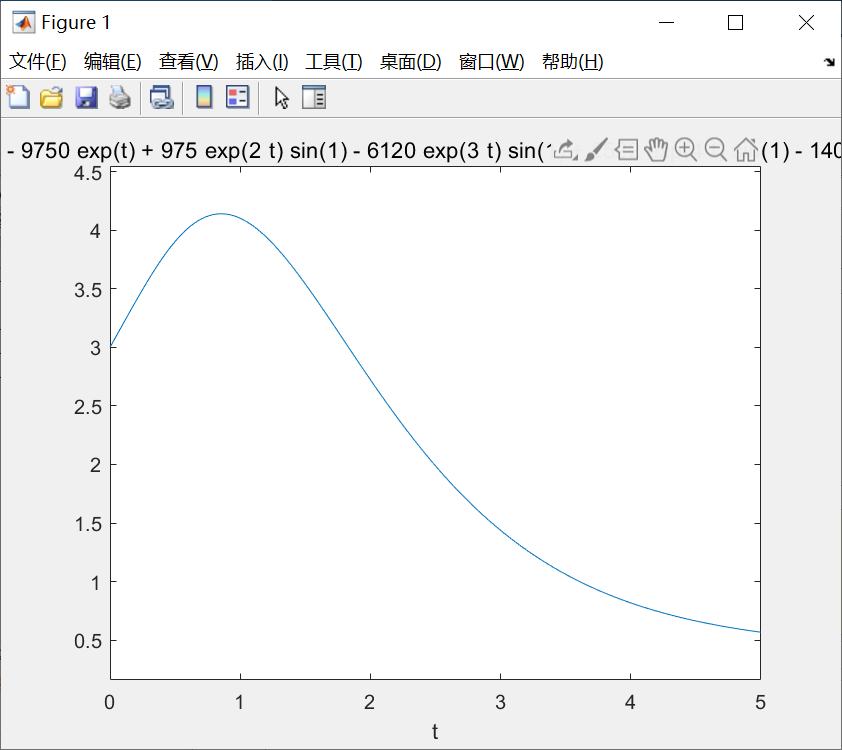
同时，我们可以处理更复杂形况下的微分方程：
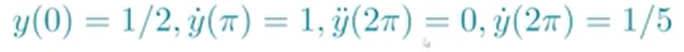
只要凑足四个独立条件，我们就可以通过通解把c1到c4的系数计算出来，最后得出原始问题的数值解。
1
2
3y=dsolve(['D4y+10*D3y+35*D2y+50*Dy+24*y=',char(uu)]),'y(0)=1/2','Dy(pi)=1','D2y(2*pi)=0','Dy(2*pi)=1/5' %由不宜读的解析解求出近似解
求解微分方程组：
例题2：
声明t为符号变量，然后用下面两个字符串描述原始的微分方程，再调用dslove函数，同样能得到原始问题的解析解。
1
2
3
4
5syms t y; %声明关键字 u=exp(-5*t)*cos(2*t+1)+5; uu=5*diff(u,t,2)+4*diff(u,t)+2*u; [x,y]=dsolve('D2x+2*Dx=x+2*y-exp(-t)','Dy=4*x+3*y+4*exp(-t)')
变系数的微分方程：
例题3：
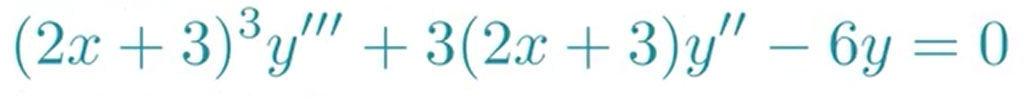
我们可能很自然的就能想到：
1
2y=dsolve('(2*x+3)^3*D3y+3*(2*x+3)*Dy-6*y') %%错误的
得到方程的一个解，但是这个解本身是错误的。因为如果要采用字符串来描述微分方程的时候，一定要注意，在描述完微分方程的之后，在语句的后面应该指明自变量是什么。
自变量为x：
1
2
3
4y=dsolve('(2*x+3)^3*D3y+3*(2*x+3)*Dy-6*y','x'); y=simplify(y),syms x; simplify((2*x+3)^3*diff(y,x,3)+3*(2*x+3)*diff(y,x)-6*y)
求解完了进行化简，再把解带入原始的方程检验一下误差。
结果：
1
2
3
4
5
6
7
8
9y = C1*(x + 3/2) - 2*C2*(x + 3/2)^(1/2) + C3*(2*x + 6)*(x + 3/2)^(1/2) ans = 0
刚才介绍的是用字符串来描述微分方程，如果用解析表达式来描述微分方程，就不用最后再指明自变量了，因为自变量已经表明了。
1
2
3syms x y(x) y=dsolve((2*x+3)^3*diff(y,3)+3*(2*x+3)*diff(y)-6*y == 0)
例题4：
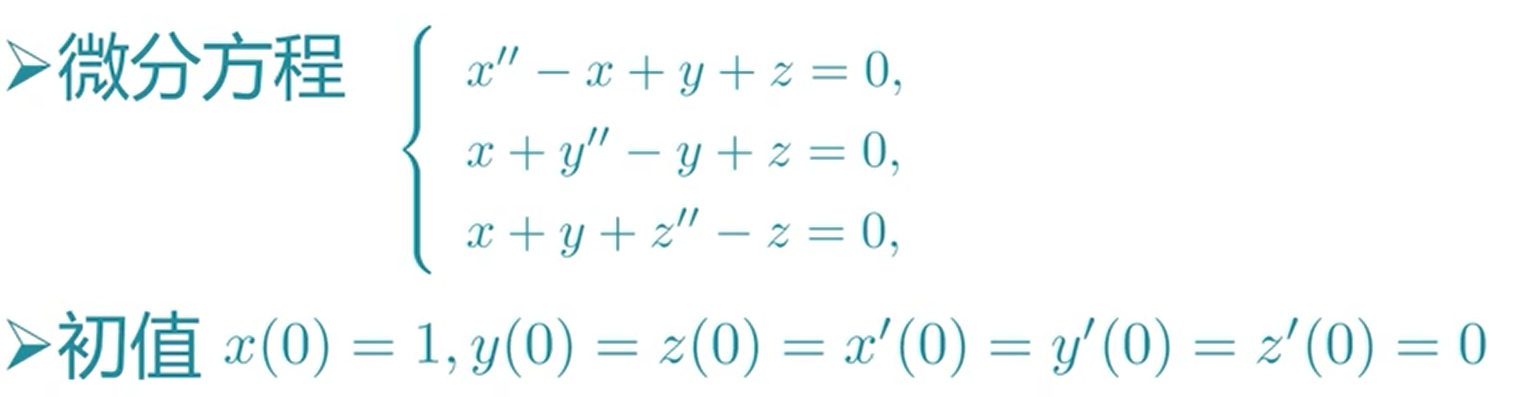
只需把三个方程用字符串描述出来，然后把六个初始条件用字符串描述出来，就可以得到方程最终的解。
1
2[x,y,z]=dsolve('D2x-x+y+z=0','x+D2y-y+z=0','x+y+D2z-z=0','x(0)=1,y(0)=0,z(0)=0','Dx(0)=0,Dy(0)=0,Dz(0)=0')
这个方程如果采用符号表达式描述微分方程要比字符串描述微分方程要麻烦一些，因为除了x和y之外，我们还需要引入一些中间变量，这样才能把原来的问题用符号表达式描述出来。
线性状态空间方程的解析解：
前半部分式子可以用expm函数来求解，后半部分可以先把被积函数计算出来，在计算定积分，就可以把解析解的出来。
例题5：
直接积分法求：
1
2
3
4
5
6
7
8
9syms t tau; u=2+2*exp(-3*t)*sin(2*t); A=[-19,-16,-16,-19;21,16,17,19;20,17,16,20;-20,-16,-16,-19]; B=[1;0;1;2]; C=[2 1 0 0]; x0=[0;1;1;2]; y=C*(expm(A*t)*x0+int(expm(A*(t-tau))*B*subs(u,t,tau),tau,0,t)); simplify(y)
结果：
1
2
3
4ans = (119*exp(-t))/8 + 57*exp(-3*t) + (127*t*exp(-t))/4 + 4*t^2*exp(-t) - (135*cos(2*t)*exp(-3*t))/8 + (77*sin(2*t)*exp(-3*t))/4 - 54
特殊非线性微分方程的解析解
只有极少数非线性微分方程可以通过dsolve函数得出解析解
例题6：
1
2
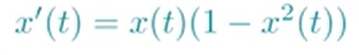
3syms t x; x=dsolve('Dx=x*(1-x^2)')
结果：
1
2
3
4
5
6
7x = 0 1 -1 (-1/(exp(C1 - 2*t) - 1))^(1/2)
若要改变原有的微分方程，使其右侧+1：
1
2
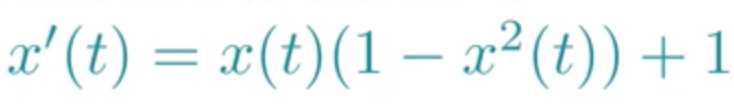
3syms t x; x=dsolve('Dx=x*(1-x^2)+1')
结果：
1
2
3
4
5
6x = root(z^3 - z - 1, z, 1) root(z^3 - z - 1, z, 2) root(z^3 - z - 1, z, 3)
这个微分方程的解析解就就不出来了,通过这个例子我们可以看出来，绝大部分微分方程是没有解析解的。
我们再看看一个著名的Van der Pol方程。
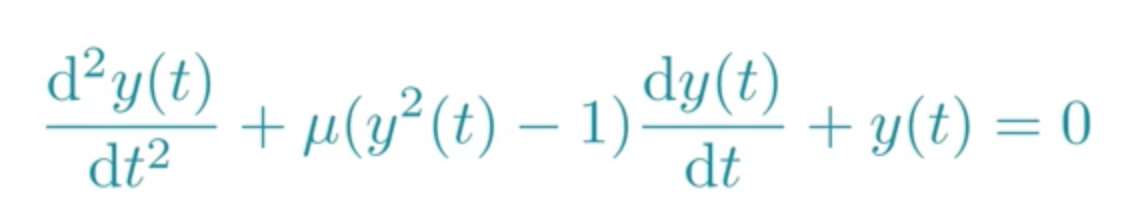
在这个方程里存在y的平方项，也存在y的平方与y的一阶导数乘积项，所以此方程为非线性微分方程。
尝试代码：
1
2
3syms t y(t) mu; y=dsolve(diff(y,2)+mu*(y^2-1)*diff(y)+y==0)
结果：
1
2
3
4
5
6
7
8警告: Unable to find explicit solution. > In dsolve (line 190) In BilibiliCode (line 56) y = [ empty sym ]
我们发现，matlab提示，方程的显式解是找不到的，换句话说，解析解是不存在的。从这个例子可以看出来，绝大部分非线性微分方程是没有办法求解的。
解析解不存在时，我们应该考虑用数值的方法来求解相应的微分方程。
后续会更新数值解相关解法。
最后
以上就是多情皮带最近收集整理的关于Matlab与微分方程解析解（dsolve）dsolve函数：求解微分方程组：变系数的微分方程：线性状态空间方程的解析解：特殊非线性微分方程的解析解的全部内容，更多相关Matlab与微分方程解析解（dsolve）dsolve函数：求解微分方程组：变系数内容请搜索靠谱客的其他文章。
发表评论 取消回复