本文主要对以下指标的计算和解释进行阐述,并使用案例说明,最后利用python编写代码进行计算:
- risk ratios and rate ratios(风险比率和比率比率,RR)
- risk difference and rate difference(风险差异和利率差异, RD)
- attributable proportion (attributable risk percent) for the exposed(风险承担的可占比例(可归属风险百分比), AP)
- population attributable risk(人口归因风险,PAF)
- odds ratio(比率, OR)
我们使用的案例如下,假设一种产品来源于两个营销渠道,我们记录了每个渠道的转化人数和未转化人数(转化可以定义为点击、充值等)
| 营销渠道 | 转化 | 未转化 | 求和 | 转化率 |
|---|---|---|---|---|
| 渠道A | 159 | 2841 | 3000 | 159/3000=5.30% |
| 渠道B | 46 | 3454 | 3500 | 46/3500=1.31% |
| 总计 | 205 | 6295 | 6500 | 205/6500=3.15% |
归因分析指标计算
1:计算Risk Ratio(风险比率)、Rate Ratio(比率)
Risk Ratio(风险比率)通常也称为Rate Ratio(比率),表示一个相对于一个因素B,另一个因素A条件下转化率相对于因素B的转化率的倍数(A,B可以理解为实验组和对照组)。
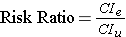
其中
C
I
e
CI_e
CIe是渠道A的转化率,
C
I
u
CI_u
CIu是渠道B的转化率。
| 营销渠道 | 转化 | 未转化 | 求和 | 转化率 |
|---|---|---|---|---|
| 渠道A | 159 | 2841 | 3000 | 159/3000=5.30% |
| 不暴露 | 46 | 3454 | 3500 | 46/3500=1.31% |
| 总计 | 205 | 6295 | 6500 | 205/6500=3.15% |
Risk Ration(RR) = 5.30%/1.31% = 4.04
解释:渠道A的转化率是不暴露组的转化率的4.04倍(Risk Ration(RR)=4.04),同时认为渠道A的转化率相比于比不暴露组的转化率提升了了404%-100%=304%(此处含义是以B为基准,相对的含义)
结论:
- 相对不暴露组的转化率而言,渠道A的转化率是不暴露组的4.04倍
- 相比于不暴露组而言,渠道A的转化率相对于B的转化率提升了304%(并不转化率是真的提升304%,而是在B的基础上提升了304%的B的转转化率)
若我们有多组实验,可以用同样的方法计算
2:计算Risk Difference(风险差异)、Rate Difference(比率差异)
Risk Difference(风险差异)也被称为Rate Difference(比率差异)
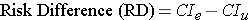
其中
C
I
e
CI_e
CIe是渠道A的转化率,
C
I
u
CI_u
CIu是不暴露组的转化率。Risk Difference(风险差异)的理解非常直观。就是直观的两个渠道转化率的差异。
由RR与RD的公式可知两者的转换关系为:
R
D
/
C
I
u
=
R
R
−
1
RD/CI_u=RR-1
RD/CIu=RR−1
利用上面例子的数据,计算出RD = 5.30%-1.31%=3.99%。代表了渠道A去渠道B的转化率差异为3.99%。
Risk Ratio与Risk Difference的出发角度不同,Risk Ratio衡量的是
渠道A相对于不暴露组提升了多少,可用于衡量改进的效果,而Risk Difference直接衡量了转化率(收益)提升了多少。Risk Ratio是相对的,Risk Difference是绝对的
3:计算Attribution Proportion
Attribution Proportion(归因分数)表示了该渠道人群中有多少是因为该渠道发生转化的。
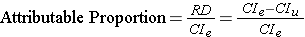
利用上面数据。计算出
A
P
=
5.30
%
−
1.31
%
5.30
%
=
75.28
%
AP = frac{5.30%-1.31%}{5.30%} = 75.28%
AP=5.30%5.30%−1.31%=75.28%
如果B代表是未参加渠道展示,则对于计算出的归因分数(Attribution Proportion),可以解释如下:渠道A展示的用户中,有75.28%的用户是因为渠道A的展示而发生了转化。
如果我们对Attribution Proportion的分子、分母同时除以
C
I
u
CI_u
CIu,则Attribution Proportion公式变为如下形式:
A
P
=
R
R
−
1
R
R
AP = frac{RR-1}{RR}
AP=RRRR−1
我们再利用新公式计算一次,利用上面计算的RR= 4.04,计算出
A
P
=
4.04
−
1
4.04
=
75.28
%
AP = frac{4.04-1}{4.04} = 75.28%
AP=4.044.04−1=75.28%
4:计算人口归因分数(PAF)
人口归因分数(PAF) Population Attributable Fraction也称为人群归因危险度PAR(Population Attributable Risk)。表示的是,所有转化人群中,有多少因为一个因素而进行转化的。
最直接的计算方式就是:渠道A转化人群占总转化人群比例*渠道A的AP,在上面例子中,转化人群中,有77.5%的人来自渠道A。因此,我们可以认为总人群中有77.5%*75.28%=58.38%的人是因为渠道A的展示发生了转化。
同时,我们也可以通过如下方式进行计算PAF
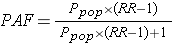
其中,
P
p
o
p
P_{pop}
Ppop =渠道A人数占总人数比例。
我们利用上面公式进行计算,先计算渠道A人数占总人数比例=3000/6500=0.4615,之后计算PAF:
P
A
F
=
0.4615
∗
(
4.04
−
1
)
0.4615
∗
(
4.04
−
1
)
+
1
=
58.38
%
PAF = frac{0.4615*(4.04-1)}{0.4615*(4.04-1)+1} = 58.38%
PAF=0.4615∗(4.04−1)+10.4615∗(4.04−1)=58.38%
计算出的PAF与上面采用直接结算得到结果是相同的。代表了,所有转化人数中,有58.38%的人是因为渠道A的展示发生了转化。
在应用中,因为转化率通常都比较低,因此,我们还可以用几率(Odds Ratio)近似代替RR,来计算每个因子的归因分数。
5:计算几率(Odds Ratio)
上面说到了,可以利用几率(Odds Ratio)近似代替RR,作为RR的估计。Odds Ratio(OR)的计算公式如下:
O
R
=
Y
1
A
/
Y
1
B
Y
2
A
/
Y
2
B
OR= frac{Y1_A/Y1_B}{Y2_A/Y2_B}
OR=Y2A/Y2BY1A/Y1B
其中Y1_A是渠道A的转化人数,Y1_B是不暴露组的转化人数,Y2_A是渠道A的未转化人数, Y2_B是不暴露组的未转化人数。
我们将上面例子数据代入计算得到:
O
R
=
159
/
46
2841
/
3454
=
4.258
OR= frac{159/46}{2841/3454} =4.258
OR=2841/3454159/46=4.258
上面已经计算出RR=4.04。对比计算结果,OR与RR的结果近似。
当用OR代替RR后,AP和PAF的估计如下:
A
P
=
O
R
−
1
O
R
AP = frac{OR-1}{OR}
AP=OROR−1
P
A
F
=
P
p
o
p
∗
(
O
R
−
1
)
P
p
o
p
∗
(
O
R
−
1
)
+
1
PAF = frac{P_{pop}*(OR-1)}{P_{pop}*(OR-1)+1}
PAF=Ppop∗(OR−1)+1Ppop∗(OR−1)
我们带入数据进行计算:
A
P
=
4.258
−
1
4.258
=
76.51
%
AP = frac{4.258-1}{4.258} =76.51%
AP=4.2584.258−1=76.51%
P
A
F
=
0.4615
∗
(
4.258
−
1
)
0.4615
∗
(
4.258
−
1
)
+
1
=
60.05
%
PAF = frac{0.4615*(4.258-1)}{0.4615*(4.258-1)+1} = 60.05%
PAF=0.4615∗(4.258−1)+10.4615∗(4.258−1)=60.05%
其中AP=76.51%代表渠道A的转化用户中有76.51%是因为渠道A展示发生了转化,PAF=60.05%代表了,所有转化用户中,有60.05%是因为渠道A发生了转化。
为什么要利用OR作为RR的近似估计去计算AP和PAF?这主要是因为,在转化率比较低的情况下(现实中转化率通常比较低),OR约等于RR。还有一个原因是,在实际中,有一些未转化人群我们是统计不到的,此时渠道A的转化率和不暴露组的转化率就无法计算,就无法准确计算RR,此时可用OR近似代替。而且在一些归隐分析模型中,例如逻辑回归等,只能通过系数 β β β计算出OR,不能直接计算出RR。
归因分析python代码
我们使用上面案例数据,数据有三列,第一列为user_id(主键),第二列为对应的营销渠道,第三列为是否转化。
导入数据后,对数据观察如下:
import pandas as pd
import numpy as np
AD_data = pd.read_csv("D:/data/Attribution_test/AD_data.csv")
print(AD_data.head(20))
接下来编写Attribution_Analysis类来进行归因分析:
import pandas as pd
import numpy as np
class Attribution_Analysis:
def __init__(self, channel, label, user_id):
self.AD_data = pd.DataFrame(np.array([channel, label, user_id]).T, columns=['channel', 'label', 'user_id'])
#计算RR
def _RR_cul(self):
self.RR=[]
for chn1, chn2 in self.channel_comb:
#计算要对比的两个渠道的转化率
rr_value = float(self.AD_count[(self.AD_count['channel']==chn1)&(self.AD_count['label']==1)]['trans_rate'])/float(self.AD_count[(self.AD_count['channel']==chn2)&(self.AD_count['label']==1)]['trans_rate'])
self.RR.append(rr_value)
print("渠道{0}相对于渠道{1}的风险比率RR为:{2}".format(chn1,chn2,self.RR[-1]))
#计算RD
def _RD_cul(self):
self.RD = []
for chn1, chn2 in self.channel_comb:
rd_value = float(self.AD_count[(self.AD_count['channel']==chn1)&(self.AD_count['label']==1)]['trans_rate'])-float(self.AD_count[(self.AD_count['channel']==chn2)&(self.AD_count['label']==1)]['trans_rate'])
self.RD.append(rd_value)
print("渠道{0}相对于渠道{1}的风险差异RD为:{2}".format(chn1,chn2,self.RD[-1]))
#计算OR
def _OR_cul(self):
self.OR = []
for chn1, chn2 in self.channel_comb:
numerator = float(self.AD_count[(self.AD_count['channel']==chn1)&(self.AD_count['label']==1)]['user_count'])/float(self.AD_count[(self.AD_count['channel']==chn2)&(self.AD_count['label']==1)]['user_count'])
denominator = float(self.AD_count[(self.AD_count['channel']==chn1)&(self.AD_count['label']==0)]['user_count'])/float(self.AD_count[(self.AD_count['channel']==chn2)&(self.AD_count['label']==0)]['user_count'])
or_value = numerator/denominator
self.OR.append(or_value)
print("渠道{0}相对于渠道{1}的几率OR为:{2}".format(chn1,chn2,self.OR[-1]))
#计算AP
def _AP_cul(self):
self.AP = []
for i in range(len(self.channel_comb)):
chn1 = self.channel_comb[i][0]
chn2 = self.channel_comb[i][1]
ap_value = (self.OR[i]-1)/self.OR[i]
self.AP.append(ap_value)
print("渠道{0}相对于渠道{1}的归因分数AP为:{2}".format(chn1,chn2,self.AP[-1]))
#计算PAF
def _PAF_cul(self):
self.PAF = []
for i in range(len(self.channel_comb)):
chn1 = self.channel_comb[i][0]
chn2 = self.channel_comb[i][1]
pop = float(self.AD_count[(self.AD_count['channel']==chn1)&(self.AD_count['label']==1)]['total_count'])/self.AD_count['user_count'].sum()
paf_value = (pop*(self.OR[i]-1))/(pop*(self.OR[i]-1)+1)
self.PAF.append(paf_value)
print("渠道{0}相对于渠道{1}的人口归因分数PAF为:{2}".format(chn1,chn2,self.PAF[-1]))
#进行归因分析
def attribution_analysis(self):
self.AD_count = self.AD_data.groupby(['channel', 'label']).count().reset_index()
self.AD_count.rename(columns={'user_id':'user_count'}, inplace = True)
self.AD_count['total_count'] = self.AD_count.groupby("channel")["user_count"].transform('sum')
self.AD_count['trans_rate'] = self.AD_count['user_count']/self.AD_count['total_count']
print("各渠道用户转化和非转化用户量为:n{}n".format(self.AD_count))
self.channel = np.unique(self.AD_count['channel'])
#用于记录渠道对比组合
self.channel_comb = []
for chn1 in self.channel:
for chn2 in self.channel:
if chn1 != chn2:
self.channel_comb.append([chn1, chn2])
self._RR_cul()
print("n")
self._RD_cul()
print("n")
self._OR_cul()
print("n")
self._AP_cul()
print("n")
self._PAF_cul()
if __name__ == "__main__":
AD_data = pd.read_csv("D:/data/Attribution_test/AD_data.csv")
attribution = Attribution_Analysis(AD_data['channel'], AD_data['label'], AD_data['user_id'])
attribution.attribution_analysis()
程序运行结果如下:
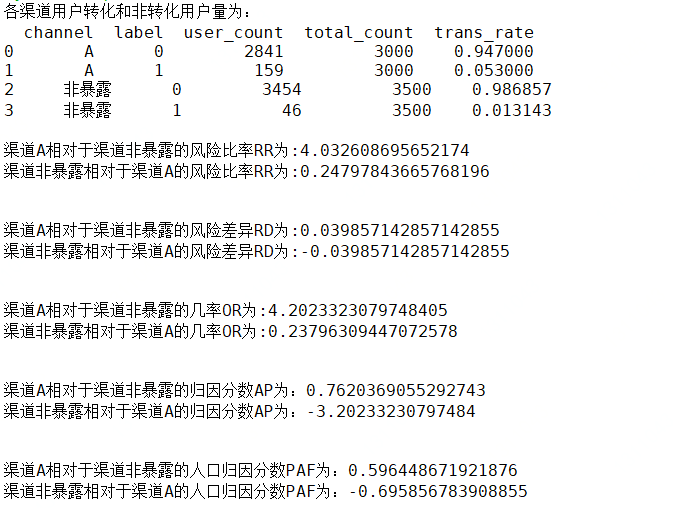
不考虑计算精度,程序计算结果与上面例子手动计算结果是相等的。
可以看到。若以不暴露组为基准(可以是基础版本或以前版本),渠道A的转化效果明显比不暴露组好,在所有转化用户中,约有60%的用户是因为渠道A的展示发生了转化。若以渠道A为基准,不暴露组的效果比较差,在所有转化用户中,因为不暴露组的展示,转化用户丢失了69%(可以理解为,若都用渠道A进行展示,转化用户还会多69%?)
最后
以上就是笨笨小猫咪最近收集整理的关于数据分析系列:归因分析原理、案例(附python代码)的全部内容,更多相关数据分析系列内容请搜索靠谱客的其他文章。








发表评论 取消回复