数据结构递归算法

一.聊聊递归。

递归算法就是将原问题不断的分解为规模更小的子问题，子问题的解题思路和原问题保持一致。当问题不断缩小规模直到一个临界点，也就是递归出口，递归出口应该存在一种简单情境，我们应该直接给出解决方案，从该点取得值再原路返回。

二.代码展示

1.使用递归算法解决累加

int addTo(int n){
	if(n<=0){
		return 0;
	}
	else{
		return addTo(n-1)+n;
	}
} 

测试代码

---- addToTest begins. ----

0 adds to 5 gets 15.

0 adds to 1 gets 1.

0 adds to -1 gets 0.
---- addToTest ends. ----

2.hanoi塔问题

                                                                图示

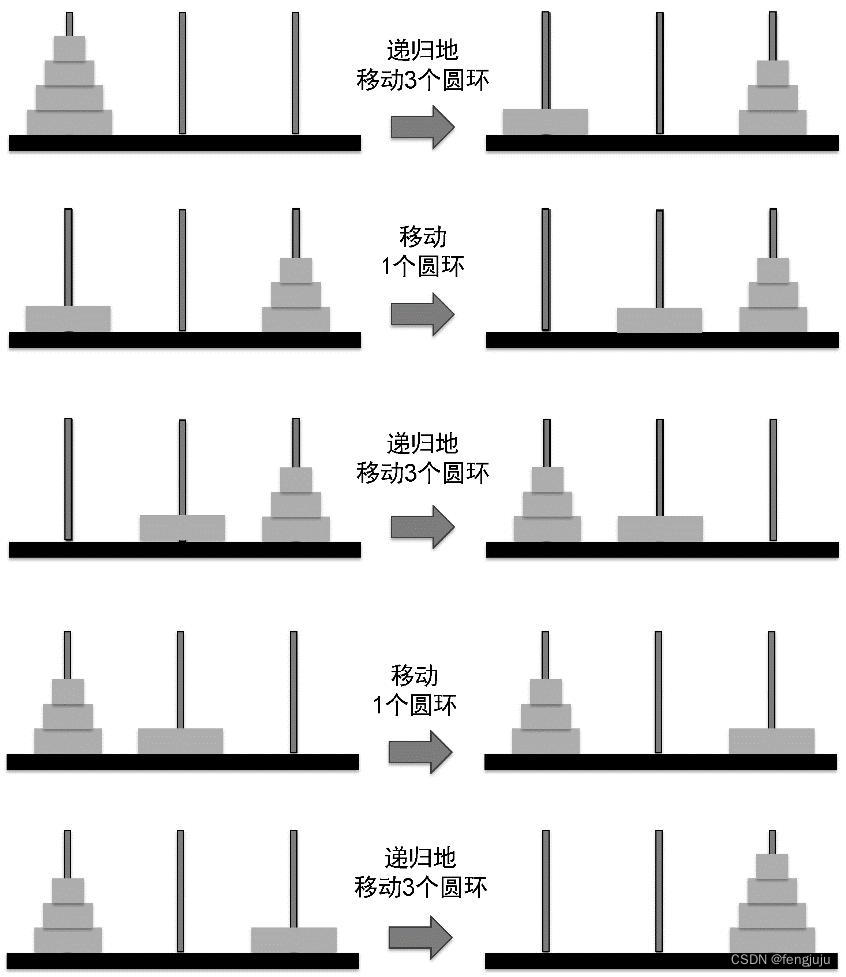
void hanoi(int n, char paraSource, char paraTransit, char paraDestination){
	if(n<=0){
		return;
	}else{
	hanoi(n-1,paraSource,paraDestination,paraTransit);
	printf("%c->%crn",paraSource,paraDestination);
	hanoi(n-1,paraTransit,paraSource,paraDestination);
	}
}

测试代码

---- hanoiTest begins. ----
2 plates
A->B
A->C
B->C
4 plates
A->B
A->C
B->C
A->B
C->A
C->B
A->B
A->C
B->C
B->A
C->A
B->C
A->B
A->C
B->C
---- hanoiTest ends. ----

二.总结

1.累加和hanoi塔问题都是达到n=0这个临界点（递归出口），此时问题的答案应该是简单清晰的。

2.Hanoi塔的时间复杂度为O(2^n），空间复杂度为O（n）。

三.附上完整代码

#include <stdio.h>

int addTo(int n){
	if(n<=0){
		return 0;
	}
	else{
		return addTo(n-1)+n;
	}
} 

void hanoi(int n, char paraSource, char paraTransit, char paraDestination){
	if(n<=0){
		return;
	}else{
	hanoi(n-1,paraSource,paraDestination,paraTransit);
	printf("%c->%crn",paraSource,paraDestination);
	hanoi(n-1,paraTransit,paraSource,paraDestination);
	}
}

void hanoiTest() {
    printf("---- hanoiTest begins. ----rn");

	printf("2 platesrn");
	hanoi(2, 'A', 'B', 'C');

	printf("4 platesrn");
	hanoi(4, 'A', 'B', 'C');

    printf("---- hanoiTest ends. ----rn");
}

void addToTest() {
	int n, sum;
    printf("---- addToTest begins. ----rn");

	n = 5;
	sum = addTo(n);
    printf("rn0 adds to %d gets %d.rn", n, sum);

	n = 1;
	sum = addTo(n);
    printf("rn0 adds to %d gets %d.rn", n, sum);

	n = -1;
	sum = addTo(n);
    printf("rn0 adds to %d gets %d.rn", n, sum);


    printf("---- addToTest ends. ----rn");
}

/**
 The entrance.
 */
int main() {
	addToTest();
	hanoiTest();
}

最后

以上就是明理金毛为你收集整理的数据结构递归算法的全部内容，希望文章能够帮你解决数据结构递归算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。