用图解决畅通工程案例与途径查找

代码中需要引入的类方法代码链接：

1. 无向图Undigraph
2. 深度优先搜索DFS与广度优先搜索BFS

畅通工程-续

介绍

• 案例和之前并查集中实现的一样，但问题略有改动，需要判断9-10城市是否相通，9-8城市是否相通：
  

使用图解决次案例：

1. 创建一个图无向图Undigraph对象 ,表示城市的图;
2. 分别调用Undigraph对象的addEdge(0,1),addEdge(6,9),addEdge(3,8),addEdge(5,11),addEdge(2,12),addEdge(6,10),addEdge(4,8) ,表示把已经修好的道路把对应的城市连接起来;
3. 通过Undigraph对象和顶点9 ,构建DepthFirstSearch对象或BreadthFirstSearch对象;
4. 调用搜索对象的marked(10)方法和marked(8)方法,即可得到9和城市与10号城市以及9号城市与8号市是否相通。

数据集

traffic.txt

20
7
0 1
6 9
3 8
5 11
2 12
6 10
4 8

Python代码实现

from Structure.graph.Undigraph import Undigraph
from Structure.graph.DepthFirstSearch import DepthFirstSearch
from Structure.graph.BreadthFirstSearch import BreadthFirstSearch

with open('../traffic.txt', 'r') as f:
    total = int(f.readline())
    UG = Undigraph(total)

    connected_nums = int(f.readline())
    for i in range(connected_nums):
        road = f.readline().split()
        UG.add_edge(int(road[0]), int(road[1]))

    city1 = 9
    city2 = 8
    city3 = 10

    print(f"----------------DFS test-----------------------")
    DFS = DepthFirstSearch(UG, city1)
    print(f"Is city[{city1}] connected with city[{city2}]? {DFS.is_marked(city2)}")
    print(f"Is city[{city1}] connected with city[{city3}]? {DFS.is_marked(city3)}")

    print(f"----------------BFS test-----------------------")
    BFS = BreadthFirstSearch(UG, city1)
    print(f"Is city[{city1}] connected with city[{city2}]? {BFS.is_marked(city2)}")
    print(f"Is city[{city1}] connected with city[{city3}]? {BFS.is_marked(city3)}")

运行结果

----------------DFS test-----------------------
Is city[9] connected with city[8]? False
Is city[9] connected with city[10]? True
----------------BFS test-----------------------
Is city[9] connected with city[8]? False
Is city[9] connected with city[10]? True

9通过6和10相连，9和8不是相通的
traffic.txt：

20
7
0 1
6 9
3 8
5 11
2 12
6 10
4 8

图的路径查找

引入

• 在实际生活中,地图是我们经常使用的一种工具,通常我们会用它进行导航,输入一个出发城市,输入-个目的地城市,就可以把路线规划好,而在规划好的这个路线上,会路过很多中间的城市。这类问题翻译成专业问题就是:从s顶点到顶点是否存在一条路径 ?如果存在,请找出这条路径。
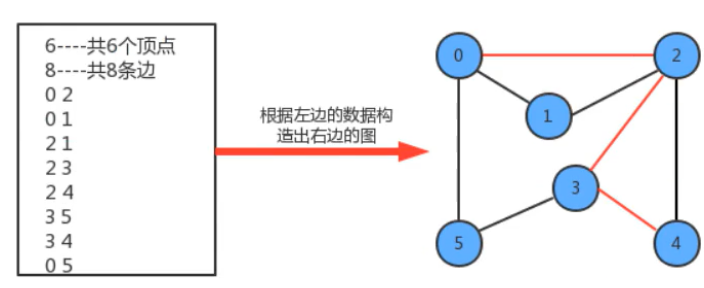  在这里我们使用的是无向图，只找出一条能够连通的道路即可，后续学习了加权路径之后在寻找指定的路径

实现步骤

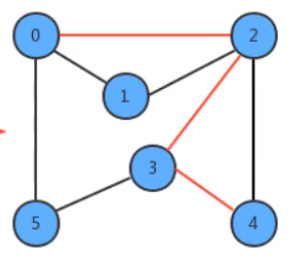
• 我们实现路径查找,最基本的操作还是遍历或搜索图,所以,我们的实现暂且基于深度优先搜索来完成。其搜索的过程是比较简单的。我们添加了edgeTo[]整型数组,这个整型数组会记录从每个顶点回到起点s的路径。如果我们把顶点设定为0 ,那么它的搜索可以表示为下图:

属性与方法设计

1. UD 接收传入的无向图
2. start 接收传入的值，作为搜索的起点
3. marked 标记是否已遍历
4. edgeTo 是一个列表，索引代表顶点，值代表当前要搜索的路径中，从起点到索引对应顶点的最后一条边，是路径实现的核心属性
5. dfs() 深度优先遍历图的顶点
6. has_path_to(v) 获取从顶点开始是否已经遍历过该传入的顶点
7. path_to(v) 获取从起点到达所传入的顶点的DFS路径

DFS.txt:

6
8
0 2
0 1
2 1
2 3
2 4
3 5
3 4
0 5

Python代码实现

from Structure.graph.Undigraph import Undigraph


class DepthFirstSearch:
    def __init__(self, graph, start):
        self.UD = graph
        self.start = start
        self.marked = [False for _ in range(self.UD.vertex)]
        self.edgeTo = [None for _ in range(self.UD.vertex)]
        self.dfs(start)

    def dfs(self, s):
        self.marked[s] = True
        edges = self.UD.get_edges_of(s)
        for e in edges:
            if not self.marked[e]:
                self.edgeTo[e] = s
                self.dfs(e)

    def has_path_to(self, v):
        return self.marked[v]

    def path_to(self, v):
        if not self.has_path_to(v):
            return
        path = [v]
        while self.edgeTo[v] != self.start:
            v = self.edgeTo[v]
            path.insert(0, v)
        path.insert(0, self.start)
        return path


if __name__ == '__main__':
    with open('../DFP.txt', 'r') as f:
        vertices = int(f.readline())
        UG = Undigraph(vertices)

        nums = int(f.readline())
        for i in range(nums):
            x, y = f.readline().split()
            UG.add_edge(int(x), int(y))

        DFP = DepthFirstSearch(UG, 0)
        print(DFP.path_to(5))

运行结果

[0, 2, 3, 5]

顺序不是唯一，跟建立边的顺序，以及设置的优先顺序也有关系，后续会学习到加了权重的边的图，则可以解决最短路径问题，引入的代码地址请回到顶部参考

最后

以上就是平淡烤鸡为你收集整理的数据结构之图：用图解决案例，Python代码实现——24用图解决畅通工程案例与途径查找的全部内容，希望文章能够帮你解决数据结构之图：用图解决案例，Python代码实现——24用图解决畅通工程案例与途径查找所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。