【信号处理】SAR 信号处理（Matlab代码实现）

86 阅读 0 评论 57 点赞

我是靠谱客的博主平淡飞鸟，最近开发中收集的这篇文章主要介绍【信号处理】SAR 信号处理（Matlab代码实现），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1 概述

2 运行结果

3 参考文献

4 Matlab代码实现

1 概述

合成孔径雷达（Synthetic Aperture Radar,SAR）图像目标检测识别技术在军事和民用等领域都发挥着重要作用。SAR图像由于存在透视收缩、叠掩、阴影等几何特点,在图像检测识别上存在许多困难。另一方面,由于SAR图像本身数据量大以及检测识别算法运算复杂等因素,进一步增大了SAR图像检测识别实时处理的难度。本文针对SAR图像目标检测识别实时处理的需求,对SAR图像目标检测识别算法进行了研究分析,研制了能满足实时处理需求的高速信号处理板卡,并基于信号处理板卡实现了检测识别算法,最后在信号处理板卡上对SAR图像检测识别算法的功能和性能进行了测试与验证。

三维加速度的存在,使CTSAR的斜距更趋复杂,从而增加了CTSAR信号处理的难度。传统直线运动轨迹合成孔径雷达（Linear Trajectory Synthetic Aperture Radar,LTSAR）下的成像算法不再适用。本课题以CTSAR高分辨率成像为目的,以频域和时-频域相结合的实时成像处理框架为前提,分析具有三维空间速度和加速度的CTSAR信号特性,并探索信号聚焦技术。首先,由CTSAR系统的几何模型,建立斜距表达式。在曲线运动轨迹模式下,结合SAR平台的运动特性,按照运动学理论,将曲线运动分解为X、Y、Z三个坐标轴方向的运动,每个方向均存在初始速度和加速度。根据三维几何模型搭建三维数学模型,构建斜距历程的函数表达式。由于机载CTSAR的复杂斜距模型限制了后续成像算法的构建,所以对该斜距模型分别进行Taylor近似和Chebyshev近似,从而降低了成像算法设计的复杂度,为CTSAR高分辨率成像算法的研究奠定基础。其次,根据机载CTSAR的斜距,建立回波信号模型。利用驻留相位原理和级数反演法将回波信号变换到二维频域,得到回波信号的二维频谱表达式。曲线历程使二维频谱的距离和方位的耦合更为复杂,增加了曲线SAR成像处理的难度。为此,论文分别利用Legendre和Chebyshev多项式对二维频谱进行正交分解近似,以达到解除耦合,实现相位补偿的目的。在此基础上,提出适用于机载CTSAR的扩展的频域成像算法,推导出了各阶相位补偿函数,实现了曲线轨迹SAR的高分辨率成像,并分析了聚焦质量。最后,针对传统Chirp Scaling成像算法无法满足具有三维速度和加速度的CTSAR的高分辨成像的现状,提出与三维曲线轨迹斜距相匹配的等效Chirp Scaling成像算法。将原始斜距等效成传统直线运动轨迹模式下的双曲斜距模型,再加上斜距补偿项。此等效斜距确保了成像的分辨率。推导了与等效斜距模型匹配的等效Chirp Scaling算法中的回波信号和频域中相应的相位函数。通过仿真实验证明,此算法的成像品质较好,满足成像要求。

2 运行结果

这里展现部分运行结果：

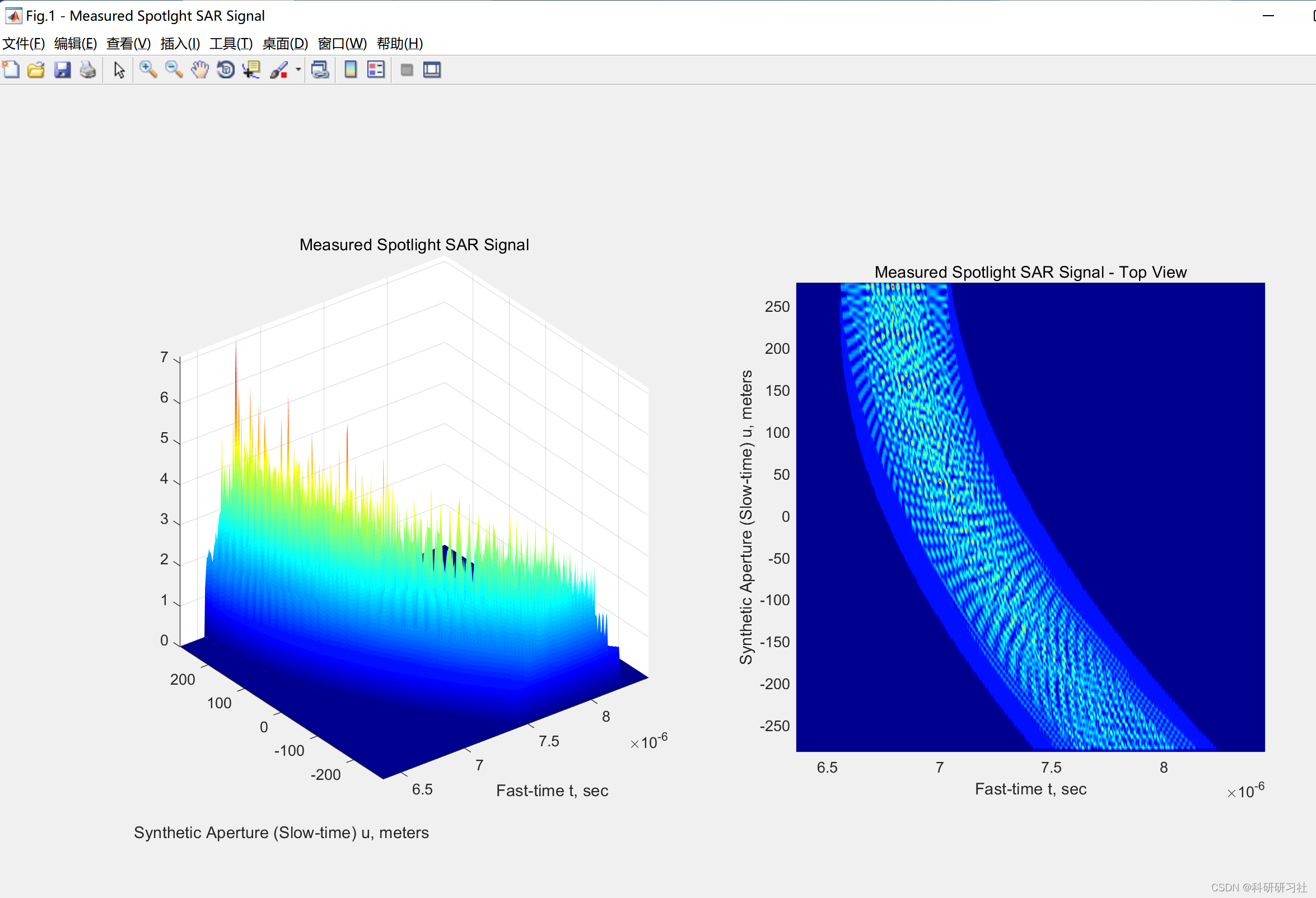
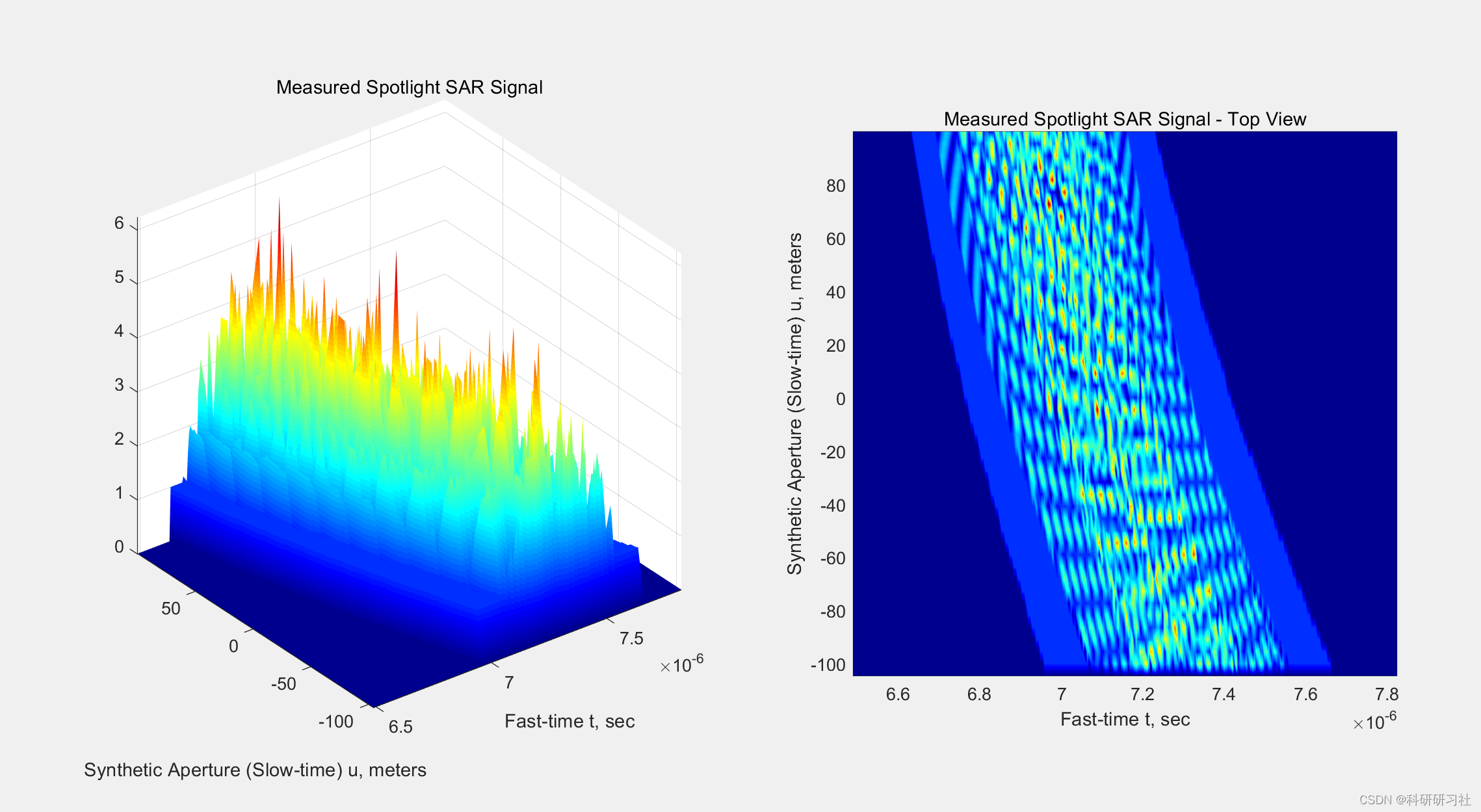
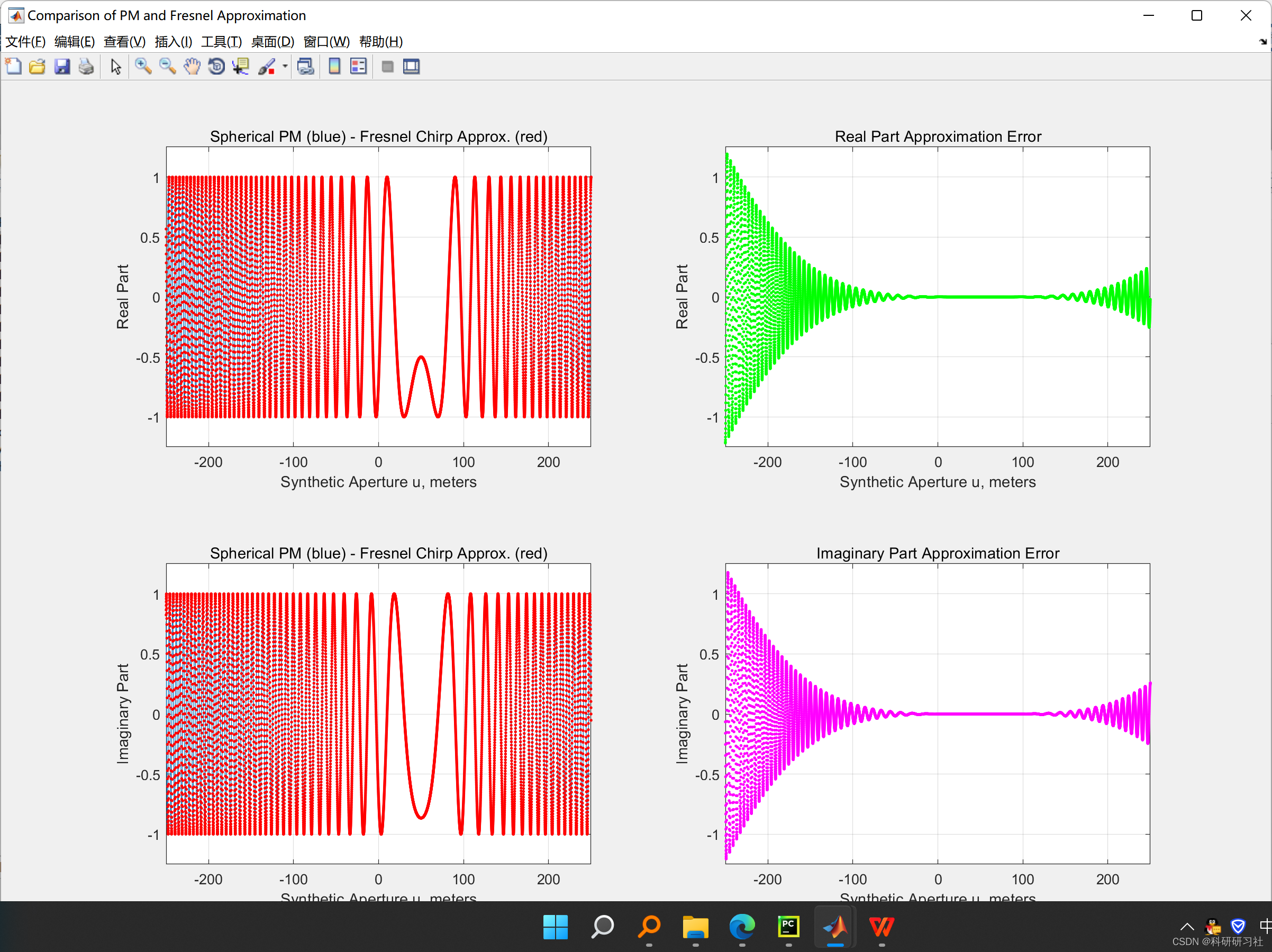
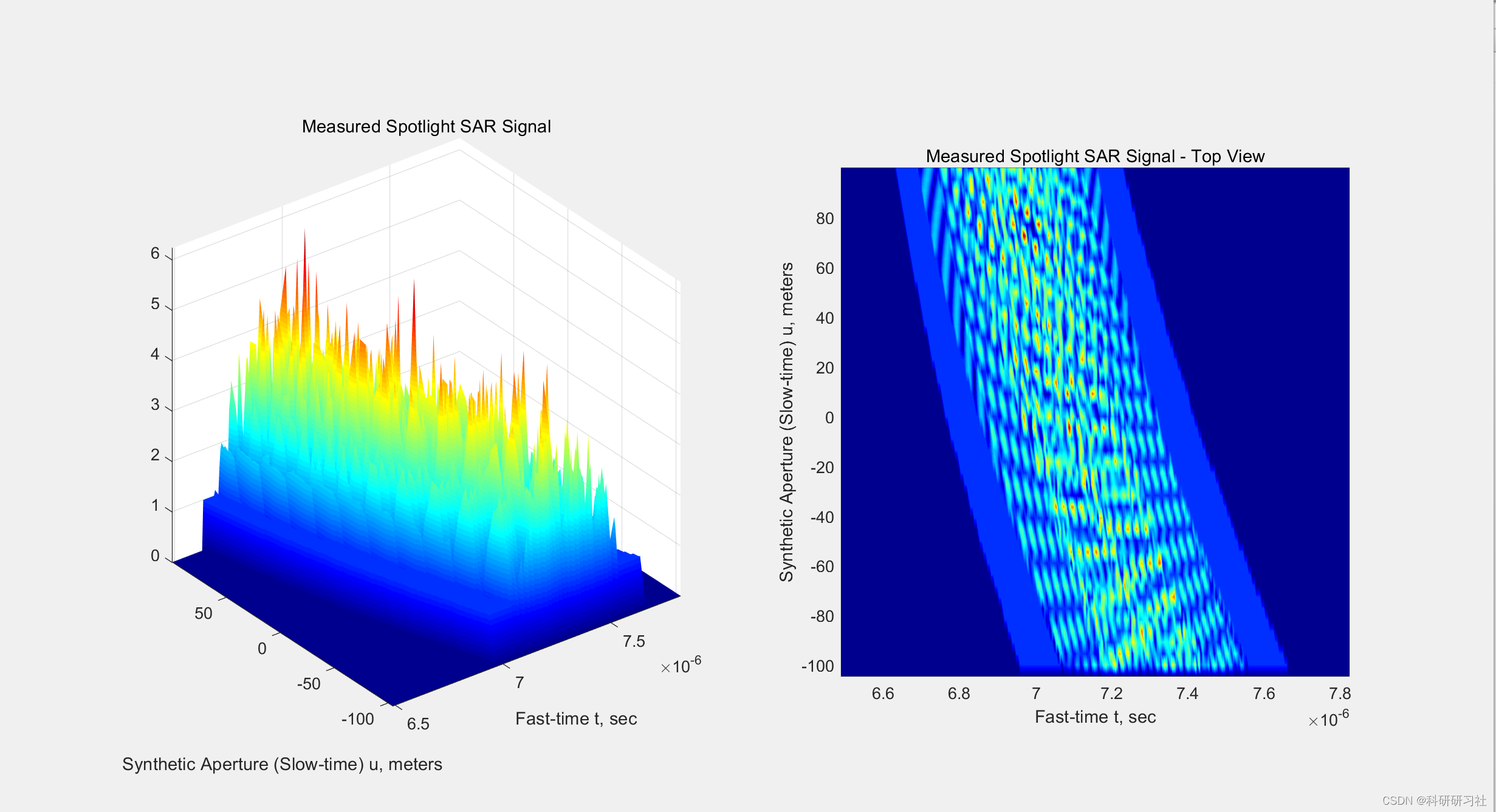
部分代码：

%% Fresnel Approximation of a PM Signal by a Chirp Signal

%% Workspace Initialization.
clc; clear; close all;

%% Radar System Parameters       
c  = 3e8;            % propagation speed
fc = 250e6;          % frequency
lambda = c/fc;       % Wavelength
k = 2*pi/lambda;     % Wavenumber
Xc = 2e3;            % Range distance to center of target area

%% Case 1: Broadside Target Area
L  = 300;             % synthetic aperture is 2*L
Y0 = 100;             % target area in cross-range is within [Yc-Y0,Yc+Y0]
Yc = 0;               % Cross-range distance to center of target area
du = 0.05;
u = -L:du:L;
xn = Xc;
yn = 50;

%% Signal Definitions - Fresnel Approximation 
% $$exp[-j2k sqrt{x_n^2 + (y_n - u)^2}] approx expBigg[-j2kx_n -
% jfrac{k(y_n - u)^2}{X_c}Bigg]$$

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%$%
%   Program to compare between the original PM signal and  %
%   Fresnel Approximation                                  %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%$%

% Original Spherical PM Signal:
PM = exp(-1i*2*k*sqrt(xn^2+(yn-u).^2));

% Fresnel Chirp Approximation:
FA = exp(-1i*2*k*(xn+((yn-u).^2)/Xc/2));

%% Plot the Spherical PM and Chirp Approximation Signals.
h1 = figure('NumberTitle', 'off','Name','Comparison of PM and Fresnel Approximation', ...
            'Position', [100 0 1200 1000]);

subplot(2,2,1)
plot(u,real(PM))
title('Spherical PM (blue) - Fresnel Chirp Approx. (red)')
hold on;
plot(u,real(FA),'r.')
xlabel('Synthetic Aperture u, meters')
ylabel('Real Part')
axis([-250 250 1.25*min(real(PM)) 1.25*max(real(PM))]);
grid on;

subplot(2,2,2)
plot(u,real(PM) - real(FA),'g.')
xlabel('Synthetic Aperture u, meters')
ylabel('Real Part')
title('Real Part Approximation Error')
grid on;
axis([-250 250 1.25*min(real(PM)) 1.25*max(real(PM))]);
grid on;

subplot(2,2,3)
plot(u,imag(PM))
hold on;
plot(u,imag(FA),'r.')
title('Spherical PM (blue) - Fresnel Chirp Approx. (red)')
xlabel('Synthetic Aperture u, meters')
ylabel('Imaginary Part')
axis([-250 250 1.25*min(imag(FA)) 1.25*max(imag(FA))]);
grid on;

subplot(2,2,4)
plot(u,imag(PM) - imag(FA),'m.')
xlabel('Synthetic Aperture u, meters')
ylabel('Imaginary Part')
title('Imaginary Part Approximation Error')
grid on;
axis([-250 250 1.25*min(imag(FA)) 1.25*max(imag(FA))]);
grid on;

%% Phase Comparison
h2 = figure('NumberTitle', 'off','Name','Comparison of PM and Fresnel Approximation', ...
            'Position', [100 0 1200 500]);

subplot(1,2,1)
plot(u,unwrap(angle(PM)))
hold on;
plot(u,unwrap(angle(FA)),'r.')
title('Phase of Spherical PM (blue) - Fresnel Chirp Approx. (red)')
xlabel('Synthetic Aperture u, meters')
ylabel('Phase (rad)')
grid on;

subplot(1,2,2)
plot(u,unwrap(angle(PM)) - unwrap(angle(FA)),'m.')
xlabel('Synthetic Aperture u, meters')
ylabel('Phase (rad)')
title('Phase Approximation Error')
grid on;