统计机器学习（三）性能度量

教程笔记概述

来源于课程MA429,讲述统计机器学习。是算法工程师的基础。

本文阅读先决条件

阅读并尽可能理解intro naive bayes.pdf这个课件。

内容总结

MSE（mean square error）

数理统计中均方误差是指参数估计值与参数值之差平方的期望值，记为MSE。MSE的值越小，说明预测模型描述实验数据具有更好的精确度。

MSE可以用来评价回归任务，也可作为损失函数。

二分类任务的混淆矩阵Confusion matrix

课件里说得很清楚了。
主要是根据TP、TN、FP、FN延伸出来的几个概念。
Success rate, accuracy：
Error rate = 1 - accuracy

这里的召回率（recall,Sensitivity,hit rate,true positive rate）比较重要，也就是所有实际的正例里正确识别的正例比例。
Tip:为什么有这些指标，因为不同场景下对分类的要求不同。比如战斗机要宁杀错不放过，TP高重要，FN多的话比较糟糕，FP找错对象，杀成了鸟。这种情况可以容忍。

F1-score以及多分类的混淆矩阵Confusion matrix

多分类混淆矩阵
f1-score等公式
多分类中f1-score对每个类别取平均值
recall 体现了分类模型H HH对正样本的识别能力，recall 越高，说明模型对正样本的识别能力越强，precision 体现了模型对负样本的区分能力，precision越高，说明模型对负样本的区分能力越强。F1-score 是两者的综合。F1-score 越高，说明分类模型越稳健。

混淆矩阵小结

实际建模过程中，我们的最终目的是找到一个符合我们标准的分类器。这个标准就是混淆矩阵制作的最大化或者最小化某个函数。

ROC curve(Receiver Operating Characteristics受试者工作特征)

直接看西瓜书。
真正例率和假正例率为什么是正相关的？
如果认为都是正例，则FN和TN都为0，也即预测的反例都为0.所以TPR和FPR都是1。
如果认为都是正例，则FP和TP都为0，也即预测的反例都为0.所以TPR和FPR都是0。

AUC

直接看西瓜书，ROC下面的面积

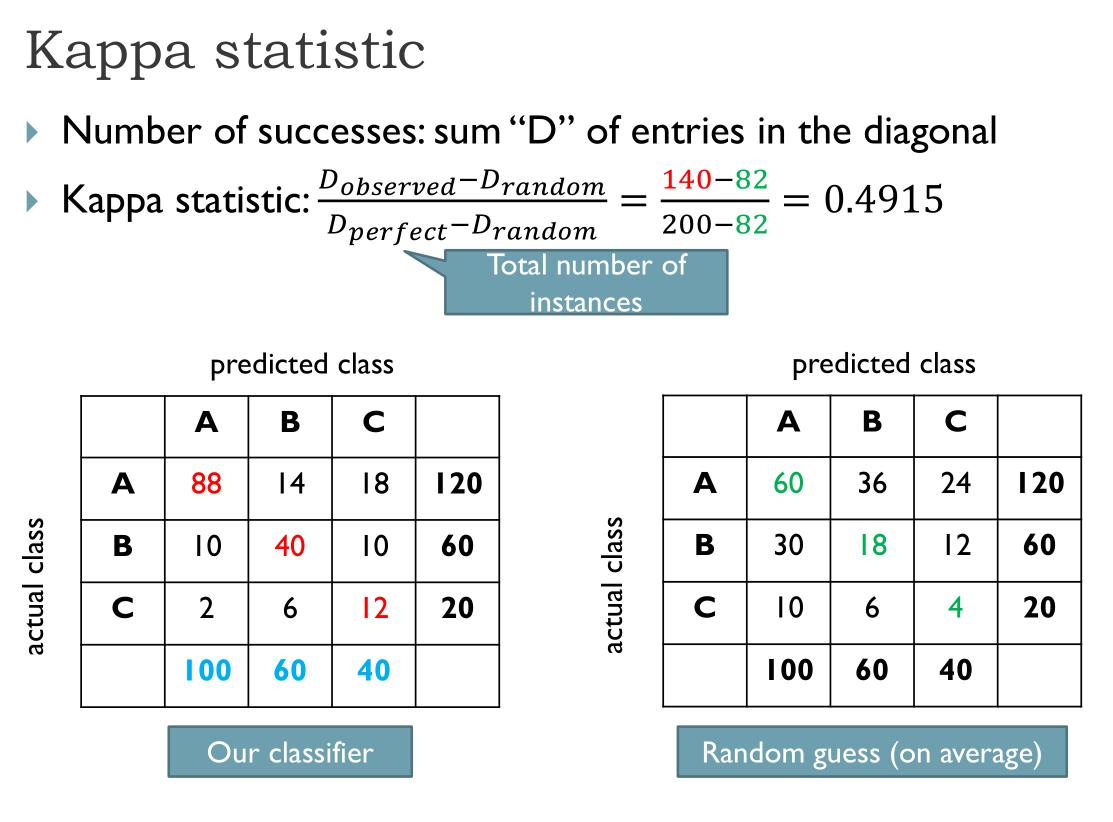
Kappa statistic

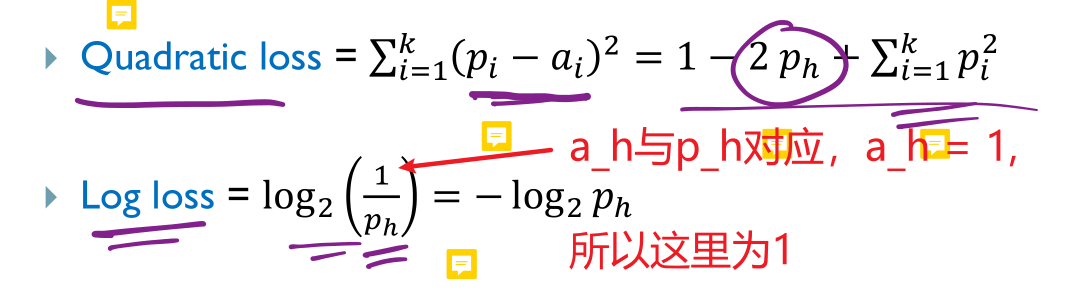
损失函数简介

真实的损失函数很多种类，这里老师给的是针对分类任务的两个损失函数的刻画。
一个k分类任务，总共有k类，分类器分类完毕之后，所有样本中分到第i类的概率是$P_i$,

但实际上，样本中第i类分类的概率应该是$a_i$，本课件中设置只有为$a_h$，其他类别概率为0。那么也就希望预测后，$P_h$尽可能大。
提出了两种损失函数：

分类时随机时的损失函数

相同的属性却具有不同的类别。此时添加随机概率$p_i^{\ast }$。
这里看不大懂了。有大手子教教我：

偏差方差分解

西瓜书里有
这个是本节课重点。

首先，有很多数据对$(x,y)$，输入x和对应的标签y，一个x可能对应多个y，因为随机噪声的影响。那么假设x和y的实际模型是：
$$y=f(x)+\epsilon (x)\text{\hspace{1em}(1)}$$
注意这里的$f$是实际的模型，是无法观测的，$\epsilon (x)$就是噪声。那么，对于一个给定的x，$f(x)$是固定的fixed，但是噪声$\epsilon (x)$不固定，我们可以认为噪声是x的函数，x大则噪声大，所以固定的f加上不固定的噪声，可能会导致相同的输入有不同的输出。
此外，噪声的平均值，也就是噪声的期望$E(\epsilon (x))=0$

我们的评估函数和评估值（也就是模型）：
$$\hat{y}={\hat{f}}_{Training}(x)\text{\hspace{1em}(2)}$$
（2）公式中的帽子(^)就代码这是预测值，和实际值有差别。然后这个模型函数${\hat{f}}_{Training}$是来自于训练数据的预测函数，并且可以有很多个训练出来的预测函数。在具体某一次训练中学习到的这个预测函数是固定的。

平均误差是：
$$\begin{array}{rl}MSE& =E(\hat{y}-y{)}^2\\ & =E{\left({\hat{f}}_{Tr}(x)-f(x)-\epsilon \right)}^2\end{array}\text{\hspace{1em}(3)}$$
也就是说，在测试集里，有很多个(x, y)，我们的模型都是固定的，所以也能得到很多个(x, y_hat)，y_hat - y再去计算均值。就可以知道在测试集上的平方误差。
在这里的随机误差，来源于两项，一是不同训练数据训练方法得到的评估函数是不同的，二是噪声每次不同。
下式为公式3：
$$MSE=E{\left(\left[{\hat{f}}_{Training}(x)-f(x)\right]-\epsilon \right)}^2\text{\hspace{1em}(3)}$$
首先有期望的公式：
$E(A-B{)}^2=E\left(A^2+B^2-2AB\right)$
$$=E\left(A^2\right)+E\left(B^2\right)-2E(A)E(B)\text{\hspace{1em}(期望的平方分解)}$$
假设AB是相互独立的：
$$E(A)E(B)=0$$
此外 ：
$$E({\epsilon }^2)=Var(\epsilon )$$
所以由期望的平方分解继续推导公式：
$$MSE=E{\left({\hat{f}}_{\pi }(x)-f(x)\right)}^2+E\left({\epsilon }^2\right)-2E\left({\hat{f}}_{\pi }(x)-f(x)\right)E(\epsilon ）$$
又$E(\epsilon ）=0$且$$E({\epsilon }^2)=Var(\epsilon )$$
所以：
$$MSE=E{\left({\hat{f}}_{\pi }(x)-f(x)\right)}^2+E\left({\epsilon }^2\right)\text{\hspace{1em}(4)}$$
继续定义：
$$\bar{\hat{f}}(x)=E\left({\hat{f}}_{Tr}(x)\right)$$
也就是说，$\bar{\hat{f}}(x)$是对于所有训练集的预测函数的均值，它是固定constant的，不是随机的。
在这里，我们加一个$\bar{\hat{f}}(x)$再减一个$\bar{\hat{f}}(x)$，
$$MSE=E([{\hat{f}}_{Training}(x)-\bar{\hat{f}}(x)]+[\bar{\hat{f}}(x)-f(x)]{)}^2+Var(\epsilon )\text{\hspace{1em}(5)}$$
右边这一项，$[\bar{\hat{f}}(x)-f(x)]$是constant，对于一个给定的x，这个表达式是恒定的，不是随机的，因为既没有噪声，也没有训练数据噪声的影响。

继续利用期望的平方公式，
这里，显然$E\left(\underline{{\hat{f}}_{Training}(x)}-\overline{\hat{f}}(x)\right)$为0，每个值减去平均值的期望就是0，所以2E(A)E(B)为0，另外，$[\bar{\hat{f}}(x)-f(x)]$是常数，所以$E[\bar{\hat{f}}(x)-f(x)]=[\bar{\hat{f}}(x)-f(x)]$
最后化解为：
$MSE=E{\left(\underline{{\hat{f}}_{Training}(x)}-\overline{\hat{f}}(x)\right)}^2+(\bar{\hat{f}}(x)-f(x){)}^2+\mathrm{var}(\epsilon )$
也就是说，MSE这个误差可以叫作泛化误差，由方差、偏差的平方以及噪声组成。

$E{\left(\underline{{\hat{f}}_{Training}(x)}-\overline{\hat{f}}(x)\right)}^2$是方差，可以写作$Var\left(\underline{{\hat{f}}_{Training}(x)}-\overline{\hat{f}}(x)\right)$,也就某次训练函数值和平均训练函数值的波动程度。刻画了不同训练数据扰动造成的影响

偏差$(\bar{\hat{f}}(x)-f(x))$：期望预测和真实结果的偏离，算法的拟合能力
噪声：期望泛化误差的下界，越高则任务越难。
希望偏差和方差都小。

Error vs flexibility

课件里说的flexibility说的应该就是对训练数据的拟合程度，越高，在测试数据的误差可能就越大。
所以，偏差越小，越flexibility

总结

朴素贝叶斯不难，关键是找一些例子，仔细计算，走一遍流程。这个PPT就不错。

最后

以上就是虚幻枕头为你收集整理的统计机器学习（三）性能度量的全部内容，希望文章能够帮你解决统计机器学习（三）性能度量所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。