MATLAB 画矢量场和轨线（可用来确定微分方程平衡点）

本方法可用于确定二元一阶微分方程平衡点

确定参数

由于笔者是在做种群竞争模型的时候想到画这个图的，故需要确定些参数

笔者取的参数如下

r1=0.5;
r2=0.5;
N1=300;
N2=500;
si1=0.5;
si2=4;

绘图

x1=0:10:500;
x2=0:10:200;
[y1,y2]=meshgrid(x1,x2);
dy1=r1*y1.*(1-y1/N1-si1*y2/N2);
dy2=r2*y2.*(1-y2/N2-si2*y1/N1);
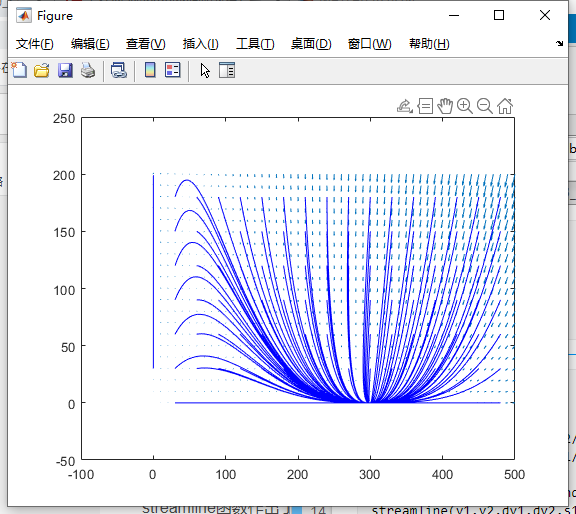
quiver(y1,y2,dy1,dy2)
[s1,s2]=meshgrid(x1(1:3:end),x2(1:3:end));
streamline(y1,y2,dy1,dy2,s1,s2)

可以看到，dy1和dy2为两个变量的导数，也就是变化率
quiver函数绘制出了各个点的导数方向（作矢量图）
streamline函数作出了指定点的轨线
因此我们看轨线的汇聚点即为微分方程的平衡点

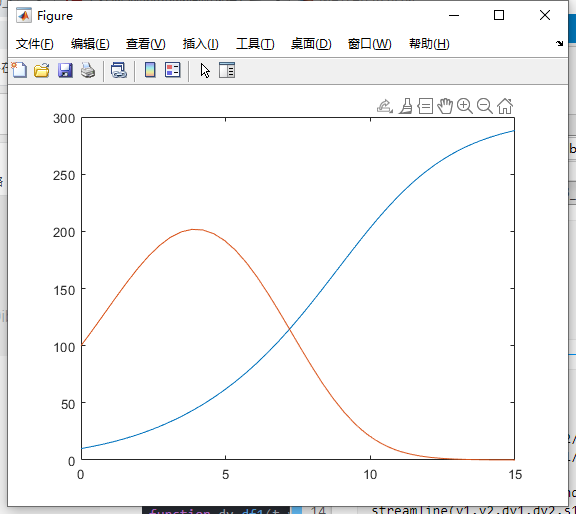
确定具体平衡点（求出具体某条轨线值）

[t,y]=ode45(@df1,[0 15],[10 100],[],r1,r2,N1,N2,si1,si2);
plot(t,y(:,1),t,y(:,2));

function dy=df1(t,y,r1,r2,N1,N2,si1,si2)
    dy=zeros(2,1);
    dy(1)=r1*y(1)*(1-y(1)/N1-si1*y(2)/N2);
    dy(2)=r2*y(2)*(1-y(2)/N2-si2*y(1)/N1);
end

最后

以上就是过时啤酒为你收集整理的MATLAB 画矢量场和轨线（可用来确定微分方程平衡点）MATLAB 画矢量场和轨线（可用来确定微分方程平衡点）的全部内容，希望文章能够帮你解决MATLAB 画矢量场和轨线（可用来确定微分方程平衡点）MATLAB 画矢量场和轨线（可用来确定微分方程平衡点）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。