到昨天，第一次实现了lattice集成后（第一阶段：无障碍物）在实车的初次运行，过程一言蔽之：基于现有的地图实现循迹功能。但是这个过程实现...累却赤激，真的是站在前辈工作上一点点进步。然后，CSDN和知乎也算同性交友平台不？本想只是记录下自己的学习过程，然后同几个同性私信分享交流经验了，哈哈，世界不孤单～总结一下这两个月的结果，希望能有更多小伙伴指点和交流。

参考源

      参考大佬们的工作是不可少的，除去之前文章里的那些参考，

      近期看了Moritz Werling经典的《Optimal trajectory generation for dynamic street scenarios in a Frenét Frame》（常看到的下图出自此论文），系统的介绍了Frenet的原理和应用，作者在验证时由简入繁，同样先验证无障碍物，然后逐步引入复杂的障碍物信息。

      另一个是百度和北大的一个免费公开课，在百度技术学院里可以直接学习：Apollo规划技术详解 花了两周时间过完，当时应该是面向本科生的吧，但是很系统，nice。

---

      实现循迹功能有很多方法，目前两种：

1. 将采好的地图直接剪裁后发给控制
2. 将地图视为参考线，基于参考线规划出轨迹发送给控制

      第1种只是应试，所以就直接略过好了～直接定位，拆分地图，分发给control即可。我们使用第2种方式，初步验证lattice planner能否正常工作。验证内容：lattice planner能否产生符合预期的轨迹；目标效果：优选出来cost最小的轨迹能够和地图很好的吻合。

开发背景

      Apollo从3.5后切换到了自研的cyberRT平台，由于时间和精力原因+学习的目的，决定将lattice planner按照自己的想法迁移出来，出发点贼单纯：我想重搭一遍然后要能在VS中断点调试....事实证明，naive啊。Apollo平台overview可看大神的帖子：解析百度Apollo之决策规划模块。

      首先，源码任务调度机制我们可以绕过，根据自己调度方法实现就行了。但是，不知道apollo中控制模块如何，规划模块中，简直了！类的各种继承，Protocol Buffer的应用以及涉及多模块交互导致数据的多样性，对于我这种弱鸡，脑壳疼，刚开始实操起来有些无从下手。

思路

      Proto香么，香。但由于不熟悉，面对两个未知的事物，一个个来。和大哥探讨了下，两个方案：

      1.apollo源码经过bazel编译后，proto会生成对应的xx.pb.h和xx.pb.c，我们直接使用编译后的成果，即把pb.cc和pb.h直接集成进来，尽可能保持planner完整性，实现快速应用lattice——实践证明，再那么下去，我们可能要搬空大半个apollo源码了，planning作为自动驾驶架构中承上启下的模块，牵扯的太多了，按照其中的继承逻辑，一眼看不到头，越过山丘..已是白头。 

      2.先整体把握lattice开发思想，然后结合源码进行理解和学习，最后假定自己在正向开发（伪正向..），把它复现。过程的确，emm，忘不了大半夜在办公室盯着满屏的红色error的无奈，对于之前用c和matlab的自己，码力产生了大的提升。额，大佬都是走1即可完成。

      最后采用的是方案2，基本路线：

      1.lattice核心分7阶段，每个阶段逐步实现，实现一个阶段遍进行相应测试，通过则继续往下推进

      2.对于proto定义的数据结构，最粗暴的方法，用结构体重写，换汤不换药。举个简单例子：

message EStop {
  optional bool is_estop = 1;
  optional string reason = 2;
}

      3.对于一些复杂的类，内部可能有数十个成员函数，一时又无法确定相应的功能。保留其框架，在后续开发中逐步填充，用到什么添加什么，毕竟任何开发都是在稳定的框架中逐渐丰富。

      由于对整个apollo的不熟悉，现在的方法可以肯定是不优的，属于只见树木不见森林，如果有趟过坑的大佬路过，希望能给予帮助~~~

正文开始

      lattice planner的启动过程就不重复了，可见上一章：Apollo中Lattice规划器结构梳理

planner->Plan(stitching_trajectory.back(), frame_.get(), ptr_trajectory_pb)

      通过Plan函数，具体为PlanOnReferenceLine()开启lattice，粗略流程如图：

      通过Plan函数，开启lattice，粗略流程如图：

0.轨迹拼接—stitching_trajectory    

      关于时间一致性问题，有很多文献有阐述，主要表现就是你的规划和车辆实际行驶轨迹不吻合。为了尽可能保证新的轨迹和上一帧规划轨迹的一致性(有论文里提到设计重合度的cost)，apollo中依据动态规划的思想(嗯..樊浩阳的视频)，以上一帧轨迹作为本周期的规划base，如何实现轨迹的拼接——找到当前车辆在上一帧轨迹中的匹配点。

      两个维度出发：时间t和历程s。

0.1查找轨迹匹配点

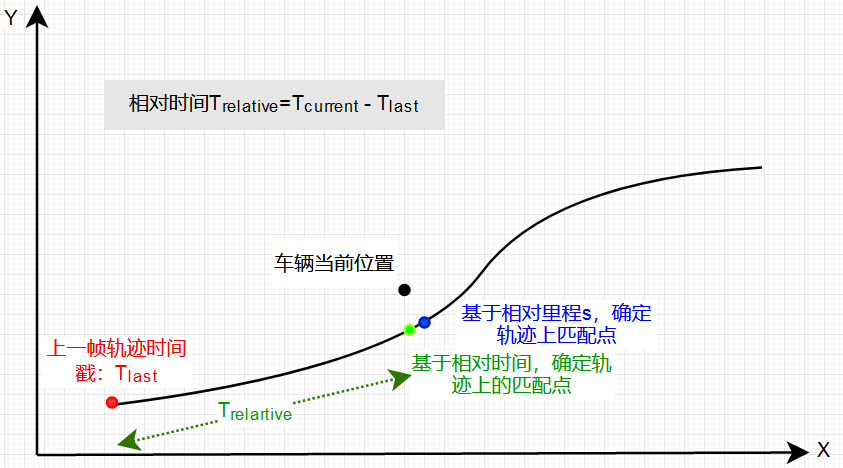
• 相对时间的匹配

      每一次轨迹生成后，含有轨迹的绝对时间即header time，和轨迹点相对于轨迹起点的相对时间relative time，所以我们可以通过时间戳

来索引到上一帧轨迹中的匹配点index。

• 相对里程的匹配

      结合自车的定位信息与上一帧轨迹信息，将自车信息从笛卡尔坐标系→Frenet坐标(s,d)，即可查询到在里程维度上的匹配点。注意一点，如果或超出一定范围，说明车辆没有按照之前规划的行驶，这时候轨迹拼接就无意义了。

• 匹配的选取

      选取min{时间匹配点，里程匹配点}作为当前车辆在上一帧映射的匹配点。

0.2拼接轨迹 & 规划起点的计算

      根据我们最终确定的匹配点，前取一定数目的轨迹点，即为我们理论上要找的stitching trajectory，那么拼接后轨迹的终点便可作为我们新一轮规划的起点，这样我们便实现了当前帧和上一帧的持续。

      重点来了，如论坛里提到的规划起点为T+dt，为何往后再推移dt时间呢？正如我们在玩LOL或dota时，假如延时500ms，我们是没有办法打好的，但不排除极端大神是可以通过超凡的预判实现游戏的操作，传说中的....让....子....弹飞....一会。planning常见执行周期为100ms，意味着当我们从开始计算，到将轨迹发给control时，已经度过了漫长的100ms，高车速时足以让车跑出去好几米了。所以应提前考虑到dt时间后车辆的大致位置。

      控制中考虑底层执行机构的延时(转向机构延时、液压回路延时)，本质上是同根吧。

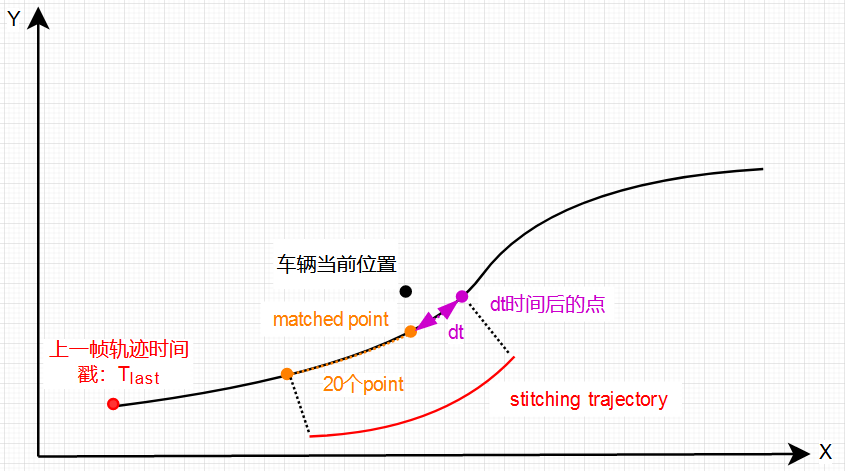
      至此，获得stitching trajectory后，其尾点(T+dt)便可作为我们本周期局部路径规划的起点，也就是后边我们常见的planning_start_point。

1.ReferenceLine的离散化    

auto ptr_reference_line =
      std::make_shared<std::vector<PathPoint>>(ToDiscretizedReferenceLine(
          reference_line_info->reference_line().reference_points()));

      referenceLine来自于Routing模块的结果，但是routing出来的path是无法让我们直接使用的，比如需要经过smoother处理才可作为原始的referenceLine进入planner（实际上我直接跳过这步了...eh，同事做的地图够光滑了，所以偷懒了）。

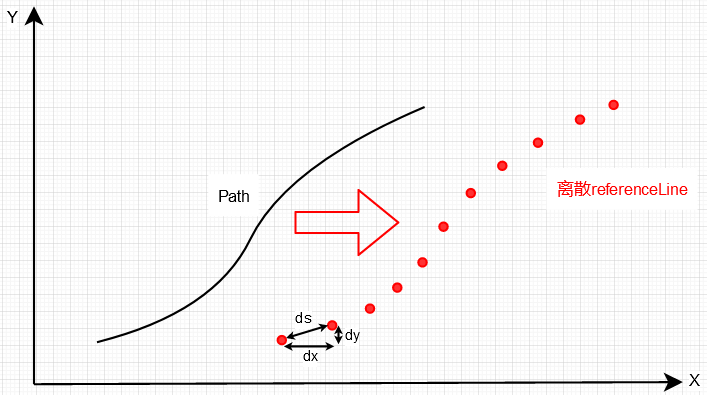
      平滑的referenceLine经过离散化形成轨迹点，我们才更好开展操作：通过差分累加获得每个点对应的里程s。作为后续的Frenet坐标系建立的前菜。

2.ReferenceLine上匹配点的检索    

PathPoint matched_point = PathMatcher::MatchToPath(
      *ptr_reference_line, planning_init_point.path_point.x,
      planning_init_point.path_point.y);

      基于离散化处理后的参考线，根据规划起点的定位数据即可找到参考线上对应的最近点，但是这个点并不能称之为匹配点，因为很可能二者连线并不是参考线的法线方向，即A和最近点B连线并不垂直参考线，当参考线的点不够密时，是存在较大误差的。

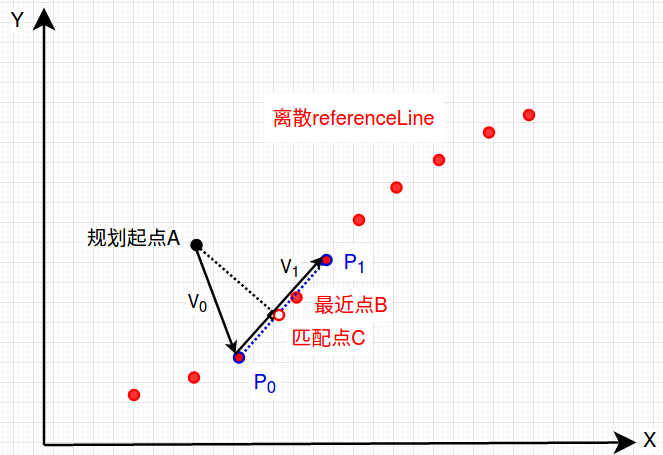
      所以又做了进一步计算，通过该最近点的前后两个点的连线，求得规划起点的位置在该连线上的垂点，则认为是匹配点。计算过程很简单，和向量运算就行了，进一步得到匹配点C的里程s信息，matched_point搞定。

3.Frenet信息初始化计算  

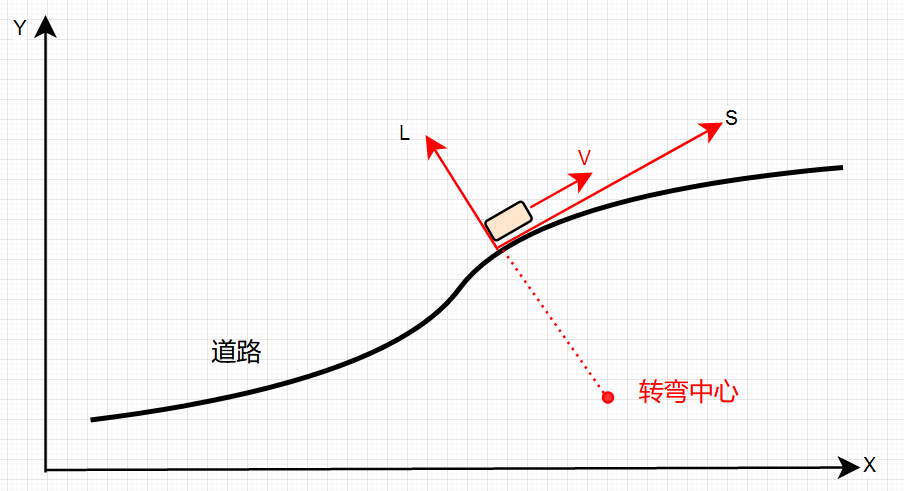
ComputeInitFrenetState(matched_point, planning_init_point, &init_s, &init_d);

      规划起始点（并不是自车当前点）在Frenet坐标中的信息，不止是(s,d)，完整的信息包括横纵向的0、1、2阶倒数，即各自对应的位移、速度和加速度，代码中int_s=[s,s',s"]和int_d=[d,d',d"]是最终将自车信息转到Frennet坐标系后的结果，即Cartesian 坐标系与Frenet坐标系的转换。注：现有车辆是通过转向轮实现转向进而产生横向运动，即车辆的横向运动是伴随纵向运动而产生的，所以横向信息d是s的因变量，为便于分辨，用l代替d，要不分不清求导d和横向d....导数也是关于s的导：。如果车辆可以独立横向运动，这个就不再适用了...例如使用了球形轮胎~

      求解过程比较有意思，看到另一个同学的推导是通过向量关系进行推导的，详情：Cartesian 坐标系与Frenet坐标系的转换。我数学比较渣，第一反应是通过运动学分析进行的推导，当然了...结果是一样的：

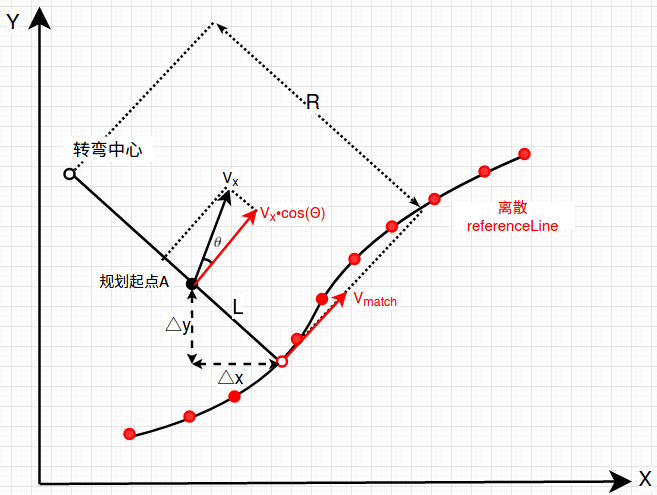
      规划起点的速度为Vx，匹配点速度Vmatch，二者夹角，即规划起点航向角和匹配点航向角的差，匹配点曲率为kr，规划起点曲率为kx，均已知，

• 求解s'，根据转弯半径R采用投影定理可得：

     

      横向距离d则直接求欧氏距离：

        左为正，右为负。

• 横向d'根据链式法则，求解：

     

      将s'带入上式可得：

• 继续求导，求解：

     

      其中，

     

      带入上式后，得到：

     

• 同理，求解：

     

      至此，笛卡尔转frenet坐标对应的六个信息：s,s',s'',d,d',d''全部获得.....int_s和int_d成为后边规划基石......凌晨一点了我擦，推的我头皮发麻。这个是基于运动学分析进行推导的，说实话出了几次岔子，若不是参照着源码中进行校正，我应该是没法一次性算对二阶导的，阿西巴。当然，有笛卡尔←→Frenet是互相可逆的。

4.解析决策，得到规划目标  

auto ptr_path_time_graph = std::make_shared<PathTimeGraph>(
      ptr_prediction_querier->GetObstacles(), *ptr_reference_line,
      reference_line_info, init_s[0], init_s[0] + FLAGS_decision_horizon, 0.0,
      FLAGS_trajectory_time_length, init_d);

       在这一阶段开始对障碍物下手，应用最多的ST图、SL图也都在此。类ptr_path_time_graph实例化后，在构造函数中就完成一系列处理了，从入参可以理解大致需求：障碍物信息基于参考线和reference_line_info（参考线车道信息，比如车道宽度等）建立相应的ST和SL图，ROI纵向的范围为[起点，起点+200m]，时距为8秒。障碍物分为三种：虚拟障碍物、静态障碍物、动态障碍物。虚拟障碍物指信号灯这些，开始静、动的学习。

      通过障碍物是否含有运动轨迹，将静态、动态障碍物区分对待。

4.1静态障碍物

      对静态障碍物的建立过程：

      1.获取障碍物多边形的所有顶点（实际上雷达是很难照射到完整障碍物的，只能探测到部分面）

      2.老方法—把所有点映射到参考线上，获得s和L，即基本的Frenet坐标，此时已经可以遍历最大最小值，形成对应的SL图了，如下右

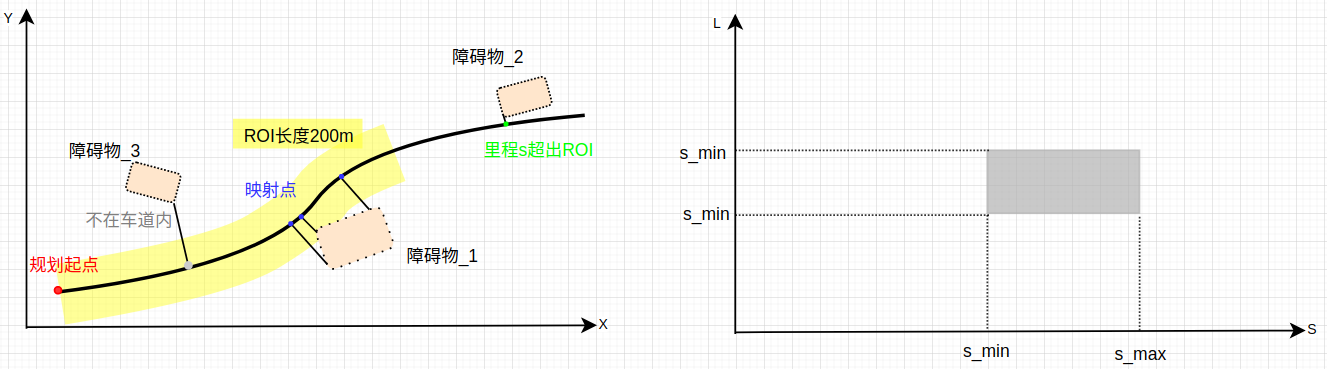
      3.障碍物超ROI范围？那就不要了—ROI范围：本车道内+纵向延伸200m。这里的SL图是根据当前时刻探测到的障碍物信息极值建立的，所以如果尝试把这SL图再还原回去，会发现.....障碍物变成了酱个样子，红框框。其实有点不严谨～意思就这个意思

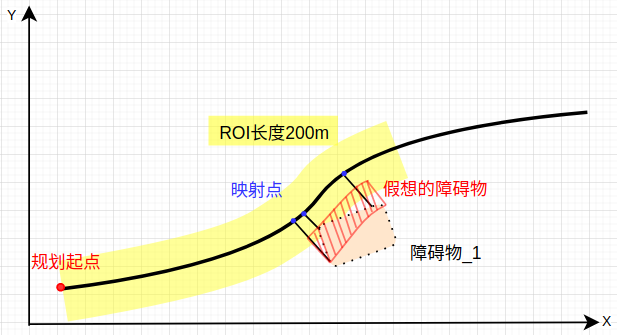
      4.静态障碍物的ST图就很直接了，ST图斜率就是目标物体的速度，因为它不动，所以它又平又直，Duang：

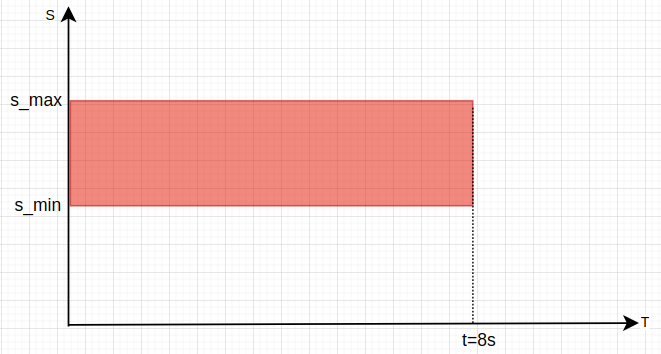
      SL，ST图的信息存储path_time_obstacle_map_，static_obs_sl_boundaries_后，静态障碍物算完结：

  path_time_obstacle_map_[obstacle_id].set_id(obstacle_id);
  //左下角
  path_time_obstacle_map_[obstacle_id].set_bottom_left_point(
      SetPathTimePoint(obstacle_id, sl_boundary.start_s(), 0.0));
  //右下角
  path_time_obstacle_map_[obstacle_id].set_bottom_right_point(SetPathTimePoint(
      obstacle_id, sl_boundary.start_s(), FLAGS_trajectory_time_length));
  //左上角
  path_time_obstacle_map_[obstacle_id].set_upper_left_point(
      SetPathTimePoint(obstacle_id, sl_boundary.end_s(), 0.0));
  //右上角
  path_time_obstacle_map_[obstacle_id].set_upper_right_point(SetPathTimePoint(
      obstacle_id, sl_boundary.end_s(), FLAGS_trajectory_time_length));
  //使用std::move(sl_boundary)将局部量sl_boundary信息掏空，然后析构掉
  static_obs_sl_boundaries_.push_back(std::move(sl_boundary));

4.2动态障碍物

      对动态障碍物的建立过程和静态类似，区别在于多了障碍物状态的查询—是基于时间戳进行的：

TrajectoryPoint point = obstacle->GetPointAtTime(relative_time);
    Box2d box = obstacle->GetBoundingBox(point);

      根据时间戳确定每一个时刻障碍物的位置，然后建立bounding box，长、宽加角度，四个顶点的坐标就可求了

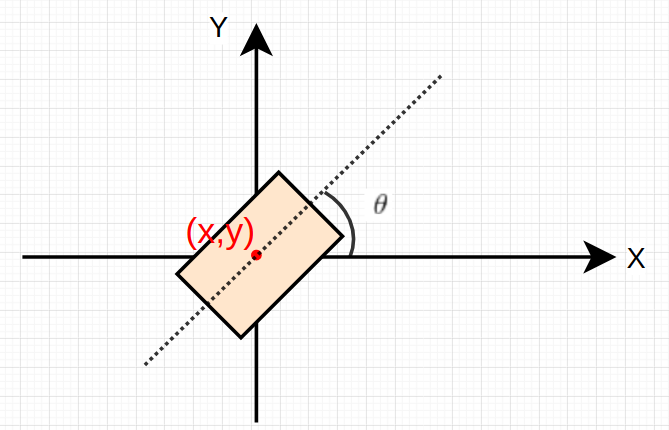
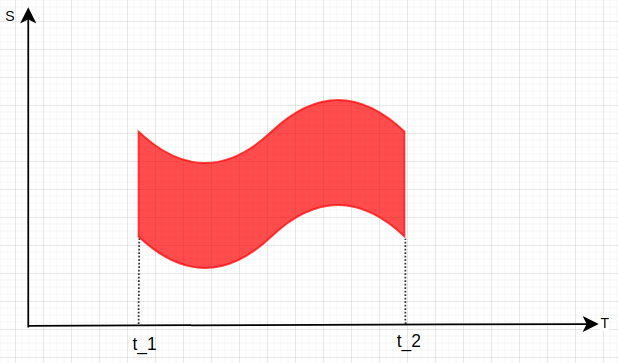
      然后来一套老办法，得到此时刻的SL与ST，反复进行时间的叠加，遍历至时长8s，apollo里timestamp步长是0.1s，够用。所以整个时间采样下来，动态障碍物的ST图便形成：

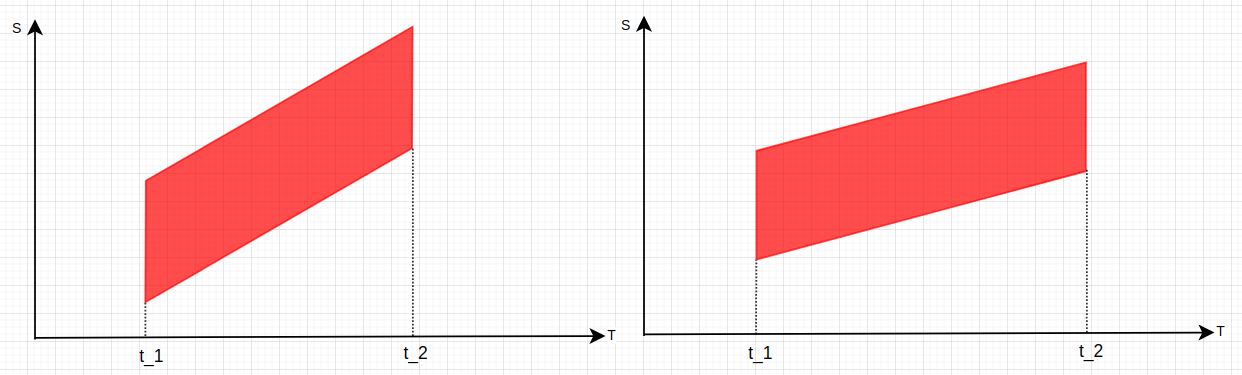
      动态障碍物的ST很可能是一会是左边这样子，一会是右边的样子，取决于感知模块给出的障碍物速度，对感知不了解只能在这猜测一下，求解惑：在检测到目标时，后续的一系列位置是基于其当前时刻的速度进行推算的，所以不会有变速的出现，就像我们在开车时是很难预测前车何时加速何时减速，变速的程度又是多少，最多预测前车匀变速运动。导致了ST图很难出现下边这样的....这行为预测得做到多牛批～

4.3动、静态障碍物信息存储

      在计算完所有障碍物信息后，存储信息即完成第4阶段。其中，SL只是对静态障碍物进行了排序存储，并没有动态目标的信息（时刻在变没有存储意义），所有障碍物的ST信息则全部压入path_time_obstacles_中实现存储。

  //使用了Lambda函数[]()，表示sort为按照sl.start_s升序
  std::sort(static_obs_sl_boundaries_.begin(), static_obs_sl_boundaries_.end(),
            [](const SLBoundary& sl0, const SLBoundary& sl1) {
              return sl0.start_s() < sl1.start_s();
            });

  for (auto& path_time_obstacle : path_time_obstacle_map_) {
    path_time_obstacles_.push_back(path_time_obstacle.second);
  }

      第4部分实质只是把感知和预测模块发过来的障碍物信息进行了格式的转换，转换为便于进行规划的形式，拥有了ST图，我们便可以开展速度的规划，是超车、跟车还是停车，ST是必不可少的一环。

      但是关于lattice中障碍物处理，目前并没有实操过...所以这一章记录的很虚，基本是把代码和查阅的资料糅杂出来的，纯属纸上谈兵，个人感想不是很多，后边实际用起来应该会有更贴切的感受。但是apollo代码初看很难受，现在真的是越来越丝滑了...

5.纵向和横向一维轨迹束的生成  

  Trajectory1dGenerator trajectory1d_generator(
      init_s, init_d, ptr_path_time_graph, ptr_prediction_querier);

  std::vector<std::shared_ptr<Curve1d>> lon_trajectory1d_bundle;
  std::vector<std::shared_ptr<Curve1d>> lat_trajectory1d_bundle;

  trajectory1d_generator.GenerateTrajectoryBundles(
      planning_target, &lon_trajectory1d_bundle, &lat_trajectory1d_bundle);

      参考线-ok，Frenet坐标系-ok，规划起点-ok，障碍物信息-ok，我们的终极目标是产生一条可行的轨迹。轨迹=纵向+横向+时间，是一个三维问题不好解，只能降维打击转换成二维问题进行解决（其实碰撞检测里的分离轴定理实质也是降维处理了），降维的好处很多，若探寻数学原理还是要看大佬们的详解了，不班门弄斧。

      轨迹的降维结果便是所谓的横纵向解耦，粗略理解：1.我先根据时间t来规划我的目标里程s—速度规划~有了！2.我再根据目标里程s来规划我的目标横向偏移量d—横向规划~有了！若感觉总有点怪怪的？I know U~（变化永远是动态的）....EM planner里的DP和QP迭代可以让我们舒服，这个是后续的学习计划。

      横纵向轨迹的生成作为类Trajectory1dGenerator的成员函数，直接调用...智能指针、Lambda函数的运用，学到了。

5.1纵向轨迹束的生成：LongitudinalTrajectoryBundle

      对于纵向轨迹，在停车和跟车状态，也都是五次多项式，但对于巡航状态，由于我们不需要确定末状态的S值，所以只有五个变量（起始点s、v、a和末点的v、a），足够用于求解四次多项式，所以采用四次多项式即Quartic polynomial。纵向轨迹实质是v-t图，即速度规划。

• 巡航状态下的纵向轨迹束

      首先不考虑障碍物信息，只考虑车辆的目标车速，以此进行速度规划：末点的采样→根据起点和末点计算四次多项式系数

void Trajectory1dGenerator::GenerateSpeedProfilesForCruising(
    const double target_speed,
    Trajectory1DBundle* ptr_lon_trajectory_bundle) const {
  ADEBUG << "cruise speed is  " << target_speed;
  auto end_conditions =
      end_condition_sampler_.SampleLonEndConditionsForCruising(target_speed);
  if (end_conditions.empty()) {
    return;
  }

  GenerateTrajectory1DBundle<4>(init_lon_state_, end_conditions,
                                ptr_lon_trajectory_bundle);
}

      对末点的采样规则：时距为8s，采样间隔1s，所以实际的采样点相对时间戳为：[0.01, 1, 2, 3, 4...7, 8]s。

      每个采样时刻进行6次采样，根据车辆的加、减速度最大值（更像是非剧烈驾驶下的最大值）以及最大巡航速度，计算该时刻车速的范围，然后均匀插入4个点，实际采样过程示意：

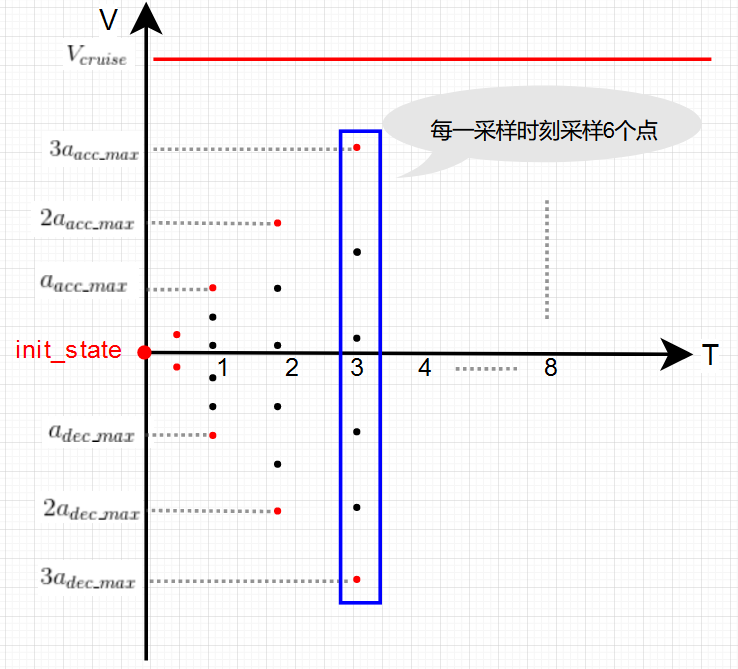
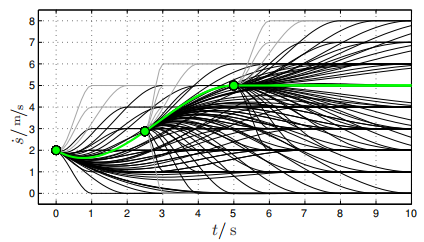
      根据首末点状态，即可求解多项式的系数。很容易看到一共产生了2+6×8=50组系数，即纵向轨迹束包含了50条纵向轨迹。在集成lattice后，我测试并输出了部分纵向轨迹束，结果如图：

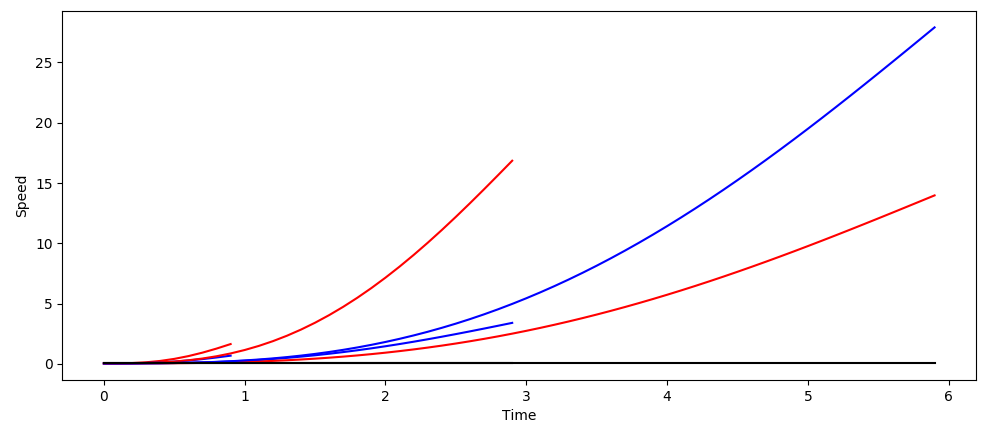
      实质上这一步只是计算并存储的了多项式系数C，并没有真实的曲线，曲线是在最终轨迹生成的时候才通过调用多项式进行的实例。

• 基于障碍物ST的纵向轨迹束

      基于障碍物的纵向规划和基于巡航规划没有本质区别，主要差异在于：末点的采样→根据起点和末点计算五次多项式系数，由四次多项式换为五次多项式。原因在于根据障碍物ST图，我们可以确定末点的s、v、a(a=0)，即明确了六个变量（起始点s、v、a和末点的s、v、a）。

void Trajectory1dGenerator::GenerateSpeedProfilesForPathTimeObstacles(
    Trajectory1DBundle* ptr_lon_trajectory_bundle) const {
  auto end_conditions =
      end_condition_sampler_.SampleLonEndConditionsForPathTimePoints();
  if (end_conditions.empty()) {
    return;
  }

  GenerateTrajectory1DBundle<5>(init_lon_state_, end_conditions,
                                ptr_lon_trajectory_bundle);
}

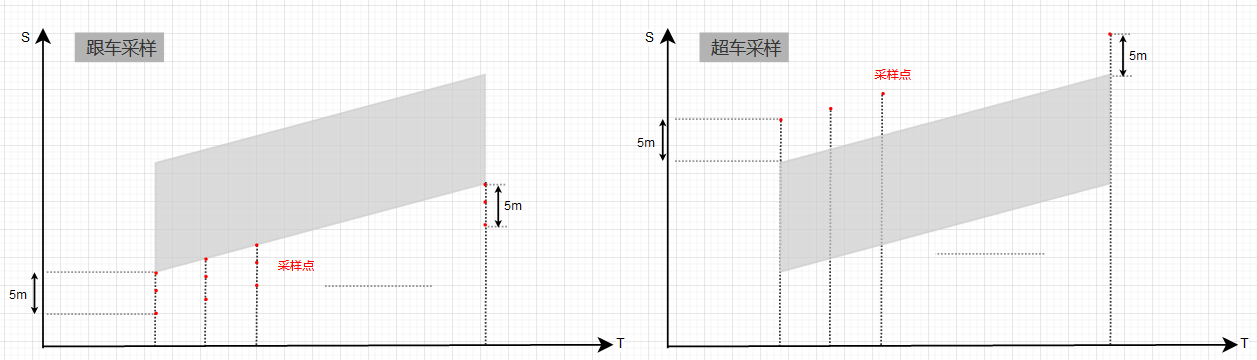
      在末点采样中，lattice的决策初露端倪~对跟车、超车分别进行采样：

QueryFollowPathTimePoints(vehicle_config, obstacle_id, &sample_points);
QueryOvertakePathTimePoints(vehicle_config, obstacle_id, &sample_points);

      二者逻辑不变，但有一点需要注意：此处是基于ST进行的采样，巡航是基于v-t进行的采样。个人理解，在lattice中，对follow和overtake的采样意味着已经在位决策做准备了，至于最终选择跟车？还是超车？根据最终轨迹的cost选择，是完成决策的最后一步。

5.2横向轨迹束的生成：LateralTrajectoryBundle

void Trajectory1dGenerator::GenerateLateralTrajectoryBundle(
    Trajectory1DBundle* ptr_lat_trajectory_bundle) const {
  if (!FLAGS_lateral_optimization) {
    auto end_conditions = end_condition_sampler_.SampleLatEndConditions();

    // Use the common function to generate trajectory bundles.
    GenerateTrajectory1DBundle<5>(init_lat_state_, end_conditions,
                                  ptr_lat_trajectory_bundle);
  } else {
    double s_min = init_lon_state_[0];
    double s_max = s_min + FLAGS_max_s_lateral_optimization;

    double delta_s = FLAGS_default_delta_s_lateral_optimization;

    auto lateral_bounds =
        ptr_path_time_graph_->GetLateralBounds(s_min, s_max, delta_s);

    // LateralTrajectoryOptimizer lateral_optimizer;
    std::unique_ptr<LateralQPOptimizer> lateral_optimizer(
        new LateralOSQPOptimizer);

    lateral_optimizer->optimize(init_lat_state_, delta_s, lateral_bounds);

    auto lateral_trajectory = lateral_optimizer->GetOptimalTrajectory();

    ptr_lat_trajectory_bundle->push_back(
        std::make_shared<PiecewiseJerkTrajectory1d>(lateral_trajectory));
  }
}

      横向轨迹规划通过S-L的关系来进行障碍物的规避，lattice中有两种方法，执行起来二选一：

      1.常规撒点采样

      看论坛里讨论比较多的-0.5、0.5啥的，主要指的就是这里，Apollo中在横向采样中对end_point进行采样按照的便是在s方向选取[10, 20, 40, 80]，每个里程点进行左右+中间三次采样，至于为什么±0.5？apollo中参考线意味着道路中心线，即车辆的规划是基于当前车道进行的，所以车辆横向偏移也应保持车辆在车道内。需要换道操作，则需要选取目标车道的中心线作为新的referenceLine了。偏移0.5的操作正是EM那篇论文里提到的nudge。

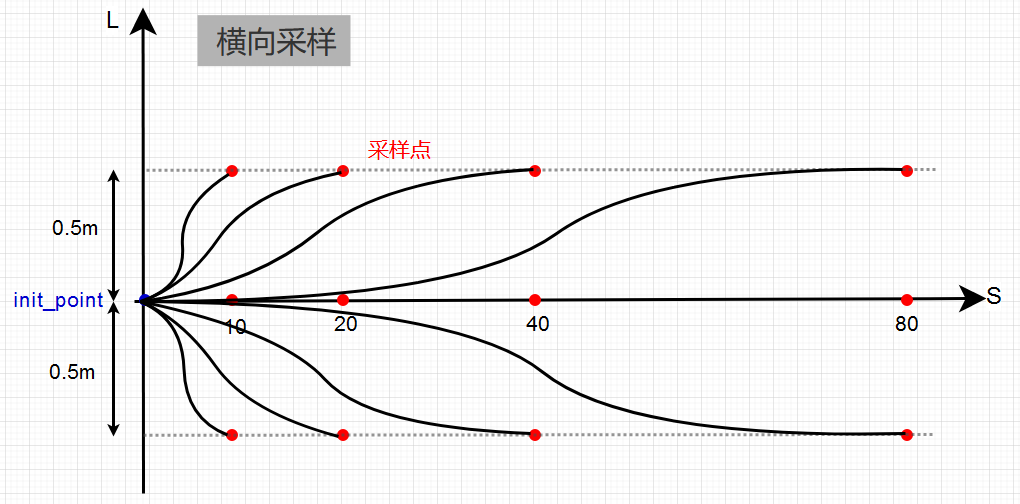
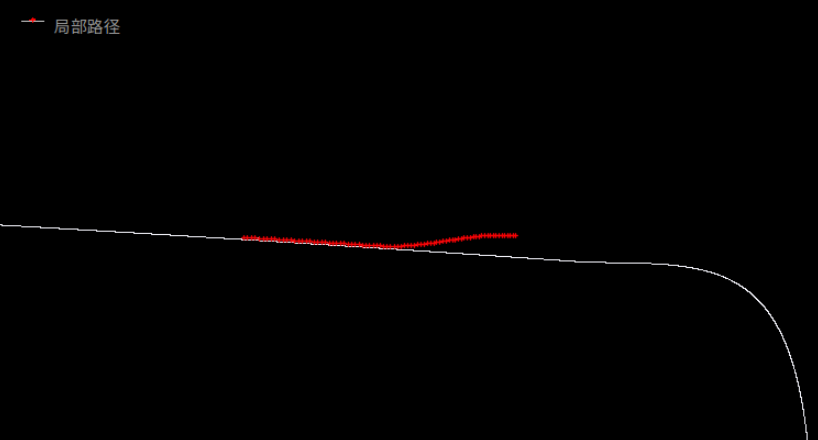
      在最近的实际操作中，由于车速较低，发现改用[5, 10, 15, 20]效果更好，明白只调这个参数肯定不对，只能说是横向轨迹的一个很重要的影响因子，包括横向采样距离，对于简单场景我们也可以不局限在本车道内，更多的采样点覆盖更多的车道，如[-1, -0.5, 0, 0.5, 1]...当然，针对简单场景而已。所以后续正式调试需要系统性的过一遍参数。下面是在实际道路上的轨迹效果。

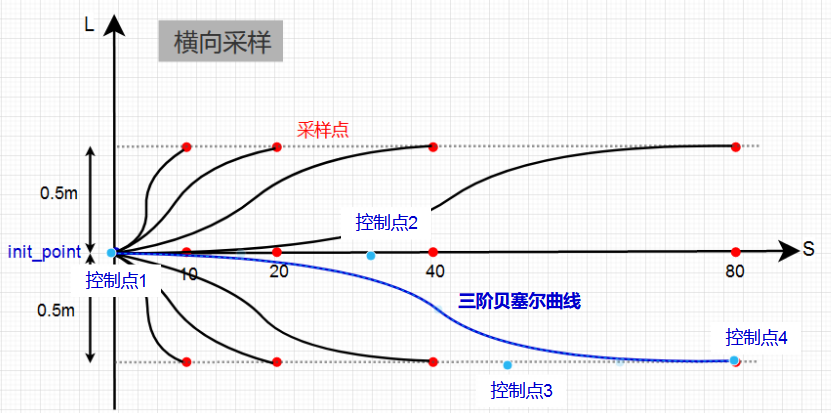
      在作图的时候发现（下图）~在画曲线的时候用的曲线工具...这不正是三阶贝塞尔曲线么，四个控制点，为何要用五次polynomial不用三阶贝塞尔曲线？A：三阶贝塞尔控制点的选取的确比较方便，但是曲线间的三阶导无法做到连续。

      对于四阶贝塞尔，查到很多论文里采用的四阶，然后通过四阶贝塞尔样条曲线进行持续性的规划。求解四阶贝塞尔存在5个控制点，和首末6个约束求解五次多项式，哪个更好一些，这个暂时就不清楚了~等大佬指导。

      在车辆初始状态偏离referenceLine 1m的时候，规划出来的部分横向轨迹如下图：

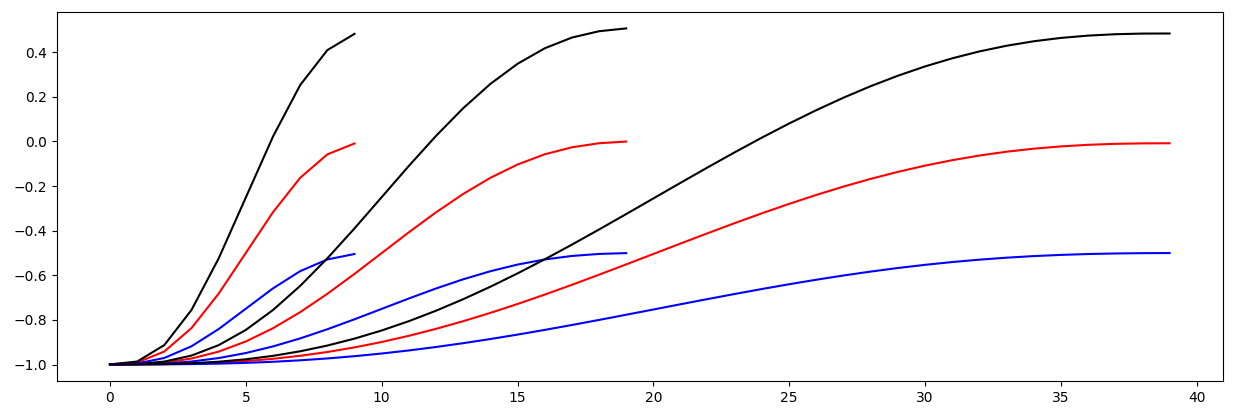
      横向采样一共产生12条结果，至此，我们便拥有了50条纵向×12条横向=600种组合。先不care，继续。

      2.使用二次规划的优化方法

      在横向规划里的else里，便是优化方法，大致这么个意思：在一段长60m的里程中，以ds=1m进行采样，遍历每个采样点的横向可达范围，即每个点的横向约束，通过这么多约束构建对应的二次型，最后通过调用OSQP进行二次规划求解...

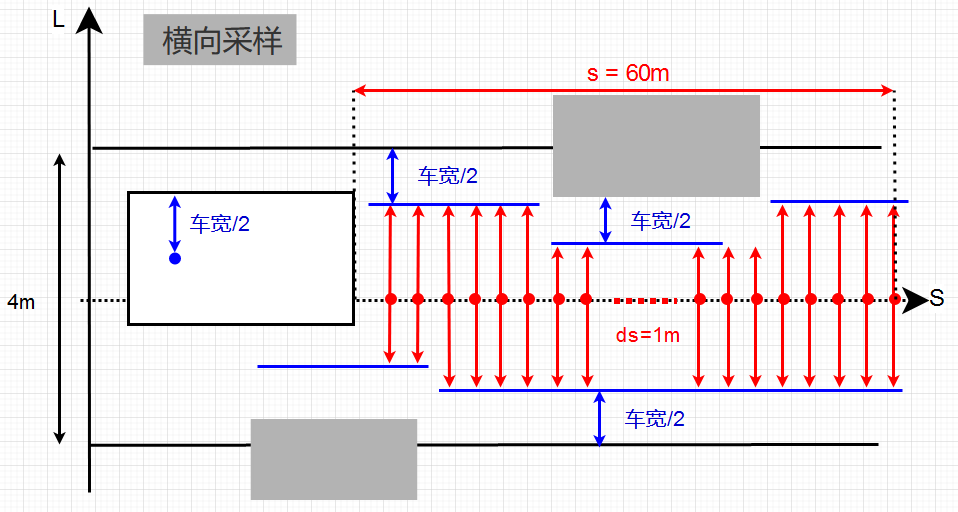
      暂时还没落实这一步，不多嘴了~OSQP求解器原理，以及常提到的牛顿快速迭代法等，详细原理有各路大神的解析，希望这一轮结束我也能写出那样的文章！

6.评价

      在刚开始学习lattice时，没有找到想象中的FSM，在EM中可以看到tsak、stage等各种显示车辆当前是换道？跟车？亦或是在哪个阶段。在早起的斯坦福的Junior中也采用的状态机（大佬对我的启蒙文：无人驾驶汽车系统入门（十九）——分层有限状态机和无人车行为规划），忘了在哪看到的观点：在一定的时期内，足够复杂的状态机是可以满足日常的自动驾驶的。ps：相对于现在流行的强化学习，我比较站这个观点，只是我这没什么理论根基，纯拍脑子。不过玩GTA时，故意堵着NPC时，听到对方的一句mother fucker然后撞开我的车扬长而去...嘴角露出一丝丝微笑，可还行~

      跑远了。在这一阶段，分两步，一个是可行性判断，第二个是cost计算。超车、跟车、停车的轨迹都会产生，至于选哪个，先cost排排好，谁低选谁，便完成了决策的过程，所以并没有出现前述的状态机。

• 首先，根据动态约束条件对一维轨迹的可行性进行评价

      直接上图了，其实就是根据车辆运动参数读纵向轨迹进行合理性校验，只有HR面通过的，才能进行下一轮技术面。在我的实操中，50条纵向经过这一步大致还幸存30多条吧，跟车型已经目标车速有关。

• 其次，评估可行的纵向和横向轨迹对，并根据成本进行排序

      这里边就是我们最常听到的cost本尊了，分别对纵、横向轨迹进行相应的cost计算，然后将cost排序，之前有梳理过：Apollo中Lattice规划器结构梳理。废话不说上图：

      纵向cost

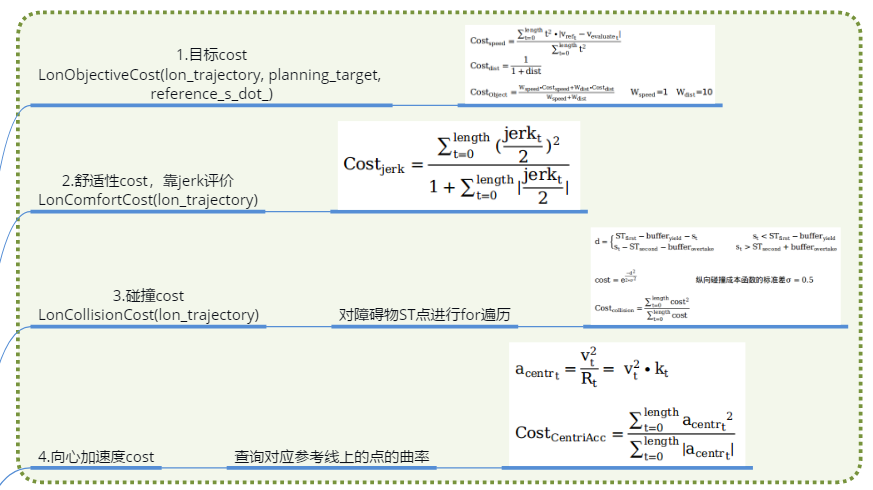
      横向cost

      关心的cost权重则在这里：

  return lon_objective_cost * FLAGS_weight_lon_objective +
         lon_jerk_cost * FLAGS_weight_lon_jerk +
         lon_collision_cost * FLAGS_weight_lon_collision +
         centripetal_acc_cost * FLAGS_weight_centripetal_acceleration +
         lat_offset_cost * FLAGS_weight_lat_offset +
         lat_comfort_cost * FLAGS_weight_lat_comfort;

      通过设计自己的cost，或者根据需求调整cost的权重，可以使轨迹符合你的实际需求，这是最近测试的一组结果：

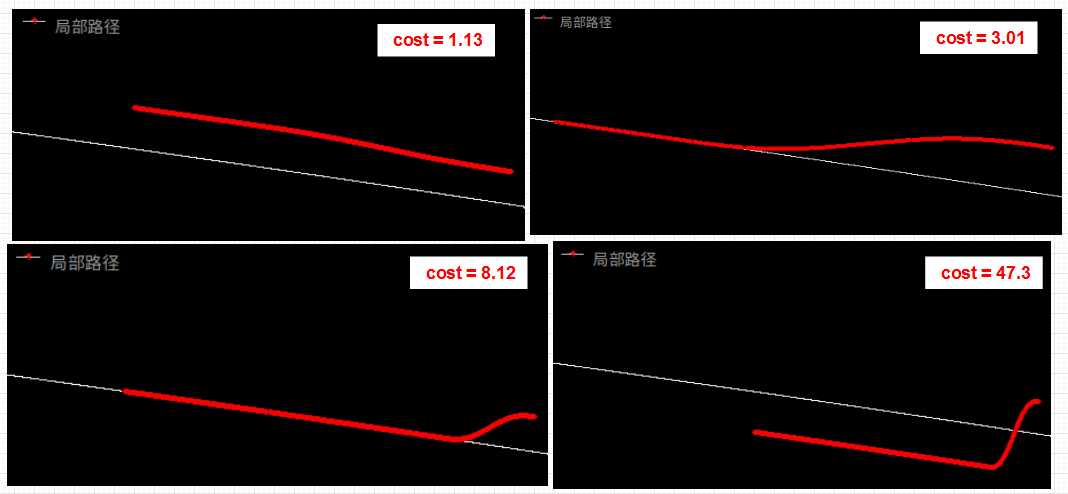
      初始车辆横向偏移量0.3m，由于舒适性cost的存在，会使车辆更偏向于选择左上的轨迹，为了让车辆优先回到车道中心线，我降低了舒适性的权重，增大了offset对应的权重，最终车辆实际产出轨迹维持在右上。当然这只是瞎xx调，后边需要认真的过一遍...那么cost暂告段落。

7.轨迹的合并、挑选 & 无碰撞轨迹的产出

      在第6步评价阶段，除了有效性检查(属于硬约束了吧)，是不会对轨迹进行删减操作的，仅仅是按cost进行排序，里边的用到了标准库的优先级队列，真香警告。唉，我这没见过世面的样子

std::priority_queue<PairCost, std::vector<PairCost>, CostComparator>
      cost_queue_;

      在第7阶段才是真正的宰杀啊，要砍掉绝大多数不合格的轨迹。这一步过程有点碎，但是都不可或缺。

7.1横纵向轨迹对的序列抽取

double trajectory_pair_cost =
        trajectory_evaluator.top_trajectory_pair_cost();

      使用了std::priority_queue队列，选择cost最小的一对小情侣下手，没啥好说的。

7.2轨迹的combine

auto combined_trajectory = TrajectoryCombiner::Combine(
        *ptr_reference_line, *trajectory_pair.first, *trajectory_pair.second,
        planning_init_point.relative_time());

      内容通俗易懂，t采样，得到s，根据s采样，得到L，然后组合得到完整的S、L、t，也没啥好解释~~Frenet坐标系下带时间戳的轨迹点

7.3轨迹合理性校验

      这一环节是大杀器，其校验内容就是这些个case，明明白白。

    auto result = ConstraintChecker::ValidTrajectory(combined_trajectory);
    if (result != ConstraintChecker::Result::VALID) {
      ++combined_constraint_failure_count;

      switch (result) {
        case ConstraintChecker::Result::LON_VELOCITY_OUT_OF_BOUND:
          lon_vel_failure_count += 1;
          break;
        case ConstraintChecker::Result::LON_ACCELERATION_OUT_OF_BOUND:
          lon_acc_failure_count += 1;
          break;
        case ConstraintChecker::Result::LON_JERK_OUT_OF_BOUND:
          lon_jerk_failure_count += 1;
          break;
        case ConstraintChecker::Result::CURVATURE_OUT_OF_BOUND:
          curvature_failure_count += 1;
          break;
        case ConstraintChecker::Result::LAT_ACCELERATION_OUT_OF_BOUND:
          lat_acc_failure_count += 1;
          break;
        case ConstraintChecker::Result::LAT_JERK_OUT_OF_BOUND:
          lat_jerk_failure_count += 1;
          break;
        case ConstraintChecker::Result::VALID:
        default:
          // Intentional empty
          break;
      }
      continue;
    }

      速度、曲率校验这些，要注意和第6阶段cost不一样的地方：此处对速度的约束不再简单的是目标车速，因为在Frenet中进行ST规划时是与真实道路曲率脱节的，而车辆在实际道路转弯时最高车速是车辆操纵稳定性与道路曲率博弈的结果，所以这一阶段的判断是要将道路实际曲率纳入范畴的。

      检测的过程代码就很直接了~

7.4轨迹的碰撞检测

collision_checker.InCollision(combined_trajectory)

      之前看论坛里有人问为何在第6步中已经进行了collision的cost计算了，还要在第7步中重复进行一遍？当时大佬的回答就是，enm...我这一节写的第一句话。哈哈...正经链接：关于Lattice Planner规划算法的若干问答

      碰撞检测采用了降维、简化等处理方式，涉及到即时间复杂度的问题，可以参拜百度公开课里樊老师的视频：《motion planning with environment》。不介意的话，也可以点一下我写的一个总结，就不在这详述了：Apollo中Lattice轨迹碰撞检测，嘿嘿。     

      其中降维和简化主要包括：

      1.车辆作为一个3D物体，我们拍扁放在二维上进行检测——降维

      2.拍扁后的车辆+障碍物，我们使用长方形bounding box（凸多边形的特性要留意）代替——简化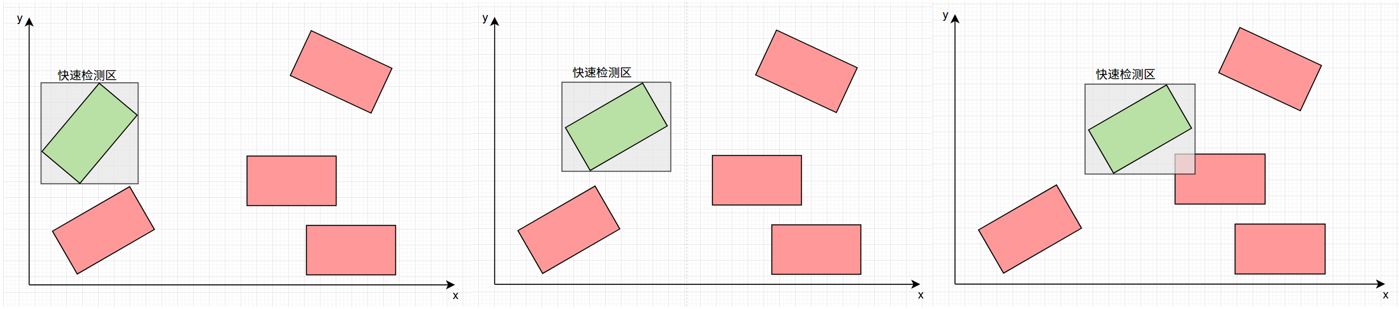

      3.对bounding box进行AABB快速检测——简化，加速

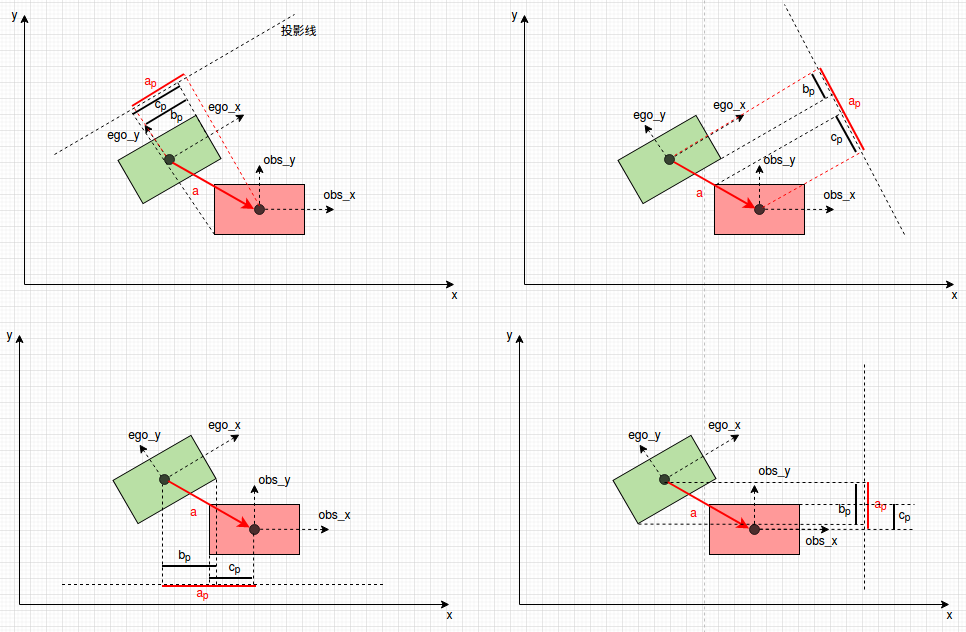
      4.对长方形进行OBB检测，二维问题将至一维空间解决——降维，确认n凸多边形无碰撞检测的最少投影次数为n——问题。

      坦白讲，这个碰撞检测自己还没进行实践检验，目前只是完成了lattice planner的第一步，无障碍物下的规划，对于障碍物的碰撞，停车点的规划以及虚拟障碍物等都只是概念上的理解，后续会逐渐加以应用。

参考线平滑的重要性

      今天在实车测试时，到一个地方总是会摆一下，后来查到是规划出来的轨迹存在阶跃，如下。刚开始想不明白，毕竟是五次多项式规划出来的，铁定是丝滑的啊，为何会有阶跃....然后才意识到，此丝滑是基于Frenet中referenceLine的丝滑，在笛卡尔中参考线本身丝滑不丝滑是不一定的。

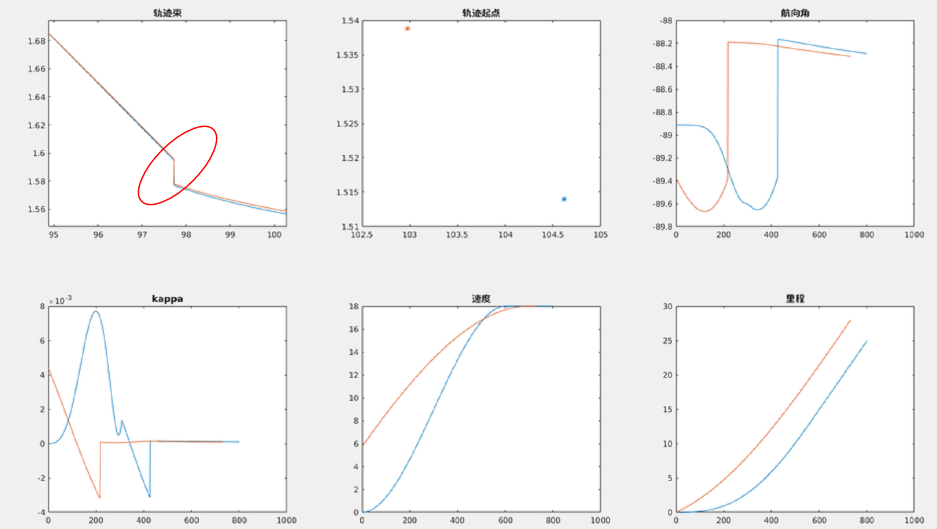
      放大使用的地图，果然~ 在实现lattice的时候，为了快速实现，所以跳过了HD map和routing模块，直接基于同事制作的地图作为参考线用了，在出现阶跃时，曲率随之出现抖动和阶跃，给控制造成了极大的难度，摆动是必然了。后期想完整的用起来，参考线的平滑处理非常之重要。

      一开始目标很明确，快速的把lattice planner在非apollo架构中运行起来，一是学习和运用lattice，另一个是学习优秀代码的风格和技巧，收获颇丰啊。

      下一阶段目标：

      1.lattice轨迹参数和权重设置的梳理+二次规划约束

      2.障碍物感知和预测信息的引入，需要多请教感知方向的大佬了

      终极目标当然是车辆在一定区域内可以自由驾驶，nudge，changelane其实足以满足半封闭区域的需求了。

      又是凌晨我擦，都怪三十而已太好看了....像海王学习

---

每天进步一点点....come on

最后

以上就是正直飞机为你收集整理的Lattice Planner从学习到放弃（一）.额不....到实践参考源开发背景正文开始的全部内容，希望文章能够帮你解决Lattice Planner从学习到放弃（一）.额不....到实践参考源开发背景正文开始所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。