python_多点拟合曲线并计算曲率半径

86 阅读 0 评论 57 点赞

我是靠谱客的博主细心硬币，最近开发中收集的这篇文章主要介绍python_多点拟合曲线并计算曲率半径，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1、摘要

本文主要讲解：python_多点拟合二次曲线，再选取两边和中点拟合圆，计算曲率半径
主要思路：

使用numpy中的np.polyfit(x, y, 2)和 np.poly1d(f1)两个函数拟合二次函数
选取拟合的二次函数中的两边和中点拟合圆
利用这三点计算曲率半径
根据这些数据画拟合图

2、数据介绍

数据可使用任何列表数据

3、相关技术

np.polyfit多项式拟合，第三个参数为x的几次幂
np.poly1d得到多项式系数
np.matmul两个numpy数组的矩阵相乘

曲率半径

最小二乘法

4、完整代码和步骤

代码输出如下：标题为曲率半径的数值
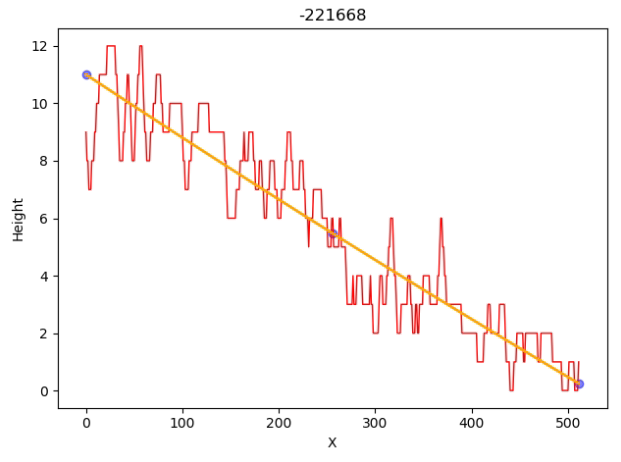
在这里插入图片描述
主运行程序入口

from math import sqrt

import numpy as np
import numpy.linalg as LA

import matplotlib.pyplot as plt
from my_utils.read_write import readCsv

src = 'D:document项目\'

def PJcurvature(x, y):
    """
        输入：三点的坐标
        输出：曲率和标准方向
    """
    t_a = LA.norm([x[1] - x[0], y[1] - y[0]])
    t_b = LA.norm([x[2] - x[1], y[2] - y[1]])

    M = np.array([
        [1, -t_a, t_a ** 2],
        [1, 0, 0],
        [1, t_b, t_b ** 2]
    ])

    a = np.matmul(LA.inv(M), x)
    b = np.matmul(LA.inv(M), y)

    kappa = 2 * (a[2] * b[1] - b[2] * a[1]) / (a[1] ** 2. + b[1] ** 2.) ** (1.5)
    return kappa, [b[1], -a[1]] / np.sqrt(a[1] ** 2. + b[1] ** 2.)


theta = [1.3, 1.3001, 1.3002]

x = 5 * np.cos(theta)
y = 5 * np.sin(theta)


# 半径 2326
def build_test():
    test = [9, 8, 8, 7, 7, 7, 8, 8, 8, 9, 9, 10, 10, 10, 11, 11, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12, 12, 12,
            12, 11, 11, 10, 9, 8, 8, 8, 8, 9, 9, 10, 10, 11, 11, 10, 10, 9, 8, 8, 8, 9, 10, 10, 11, 11, 12, 12, 12, 11,
            10, 9, 9, 8, 8, 8, 8, 9, 9, 9, 10, 10, 10, 11, 11, 11, 11, 11, 10, 10, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10,
            10, 10, 10, 10, 10, 10, 10, 10, 10, 9, 8, 8, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10,
            10, 10, 10, 10, 10, 10, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 8, 8, 7, 6, 6, 6, 6, 6, 6, 6, 6, 6,
            7, 7, 7, 7, 8, 8, 8, 8, 9, 8, 8, 8, 8, 9, 9, 9, 9, 9, 8, 8, 7, 7, 7, 7, 8, 8, 8, 7, 7, 6, 6, 6, 7, 7, 7, 8,
            8, 8, 8, 8, 7, 7, 7, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 9, 9, 9, 9, 8, 8, 7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 7, 7,
            6, 6, 6, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 6, 6, 6, 6, 6, 5, 5, 5, 5, 6, 6, 5, 5, 5, 5, 5, 5, 6,
            6, 5, 5, 5, 5, 5, 4, 3, 3, 3, 3, 3, 3, 4, 3, 3, 3, 4, 4, 4, 4, 4, 4, 3, 3, 3, 3, 3, 3, 3, 3, 4, 3, 3, 2, 2,
            2, 2, 2, 2, 3, 4, 4, 4, 3, 3, 3, 3, 4, 4, 5, 5, 6, 6, 6, 5, 4, 4, 3, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 4, 4,
            4, 3, 3, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 5, 6, 6, 5, 5,
            4, 4, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1,
            1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 2, 1, 1, 1, 1, 0, 0, 0, 0,
            1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 2, 2, 2, 2,
            2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1]
    x = [i for i in range(len(test))]
    return [x, test]



def build_function(x, y):
    f1 = np.polyfit(x, y, 2)
    print('参数 :n', f1)
    p1 = np.poly1d(f1)
    print('y=', p1)
    yvals = p1(x)  # 拟合y值
    print('yvals is :n', yvals)
    length = len(x)
    nhx = [x[0], x[int(length / 2)], x[length - 1]]
    nhy = [yvals[0], yvals[int(length / 2)], yvals[length - 1]]
    kappa, norm = PJcurvature(nhx, nhy)
    r = int(1 / kappa)
    title = '曲率半径(' + str(r) + ')'
    plt.plot(x, y, color="red", linewidth=1)
    plt.scatter(nhx, nhy, color="blue", alpha=0.5)
    plt.plot(x, yvals, color="orange", linewidth=2)
    plt.title(str(r))
    plt.ylabel('Height')
    plt.xlabel('X')
    filename = 'D:document\' + title
    plt.savefig(filename)
    plt.show()
    return p1

data = build_test()
build_function(data[0], data[1])