此系列属于胡寿松《自动控制原理题海与考研指导》(第三版)习题精选,仅包含部分经典习题,需要完整版习题答案请自行查找,本系列属于知识点巩固部分,搭配如下几个系列进行学习,可用于期末考试和考研复习。
自动控制原理(第七版)知识提炼
自动控制原理(第七版)课后习题精选
自动控制原理(第七版)附录MATLAB基础
第七章:线性离散系统的分析与校正
Example 7.1
根据定义: E ∗ ( s ) = ∑ n = 0 ∞ e ( n T ) e − n T s E^*(s)=displaystylesum_{n=0}^{infty}e(nT){rm e}^{-nTs} E∗(s)=n=0∑∞e(nT)e−nTs,确定下列函数的 E ∗ ( s ) E^*(s) E∗(s)和闭合形式的 E ( z ) E(z) E(z).
- e ( t ) = cos ω t e(t)=cosomega{t} e(t)=cosωt;
- E ( s ) = 1 ( s + a ) ( s + b ) E(s)=displaystylefrac{1}{(s+a)(s+b)} E(s)=(s+a)(s+b)1;
解:
-
e ( t ) = cos ω t e(t)=cosomega{t} e(t)=cosωt;
欧拉公式:
cos ω t = e − j ω t + e j ω t 2 cosomega{t}=frac{{rm e}^{-{rm j}omega{t}}+{rm e}^{{rm j}omega{t}}}{2} cosωt=2e−jωt+ejωt
由定义:
E ∗ ( s ) = ∑ n = 0 ∞ cos n ω t e − n s T = ∑ n = 0 ∞ ( e − j ω n T + e j ω n T 2 ) e − n s T = 1 2 ∑ n = 0 ∞ ( e j ω n T e − n s T + e − j ω n T e − n s T ) = 1 2 ( 1 1 − e j ω t e − s T + 1 1 − e − j ω t e − s T ) E ( z ) = 1 2 ( 1 1 − e j ω t z − 1 + 1 1 − e − j ω t z − 1 ) = z ( z − cos ω t ) z 2 − 2 z cos ω t + 1 begin{aligned} E^*(s)&=sum_{n=0}^{infty}cos{n}omega{t}{rm e}^{-nsT}=sum_{n=0}^{infty}left(frac{{rm e}^{-{rm j}omega{nT}}+{rm e}^{{rm j}omega{nT}}}{2}right){rm e}^{-nsT}\\ &=frac{1}{2}sum_{n=0}^{infty}({rm e}^{{rm j}omega{nT}}{rm e}^{-nsT}+{rm e}^{-{rm j}omega{nT}}{rm e}^{-nsT})=frac{1}{2}left(frac{1}{1-{rm e}^{{rm j}omega{t}}{rm e}^{-sT}}+frac{1}{1-{rm e}^{{-rm j}omega{t}}{rm e}^{-sT}}right)\\ E(z)&=frac{1}{2}left(frac{1}{1-{rm e}^{{rm j}omega{t}}z^{-1}}+frac{1}{1-{rm e}^{{-rm j}omega{t}}z^{-1}}right)=frac{z(z-cosomega{t})}{z^2-2zcosomega{t}+1} end{aligned} E∗(s)E(z)=n=0∑∞cosnωte−nsT=n=0∑∞(2e−jωnT+ejωnT)e−nsT=21n=0∑∞(ejωnTe−nsT+e−jωnTe−nsT)=21(1−ejωte−sT1+1−e−jωte−sT1)=21(1−ejωtz−11+1−e−jωtz−11)=z2−2zcosωt+1z(z−cosωt) -
E ( s ) = 1 ( s + a ) ( s + b ) E(s)=displaystylefrac{1}{(s+a)(s+b)} E(s)=(s+a)(s+b)1;
将 E ( s ) E(s) E(s)展成部分分式,有:
E ( s ) = k 1 s + a + k 2 s + b , k 1 = 1 b − a , k 2 = 1 a − b E(s)=frac{k_1}{s+a}+frac{k_2}{s+b},k_1=frac{1}{b-a},k_2=frac{1}{a-b} E(s)=s+ak1+s+bk2,k1=b−a1,k2=a−b1
有
e ( t ) = k 1 e − a t + k 2 e − b t e(t)=k_1{rm e}^{-at}+k_2{rm e}^{-bt} e(t)=k1e−at+k2e−bt
经采样拉普拉斯变换,可得:
E ∗ ( s ) = k 1 1 − e − a T e − s T + k 2 1 − e − b T e − s T E^*(s)=frac{k_1}{1-{rm e}^{-aT}{rm e}^{-sT}}+frac{k_2}{1-{rm e}^{-bT}{rm e}^{-sT}} E∗(s)=1−e−aTe−sTk1+1−e−bTe−sTk2
故有
E ( z ) = k 1 1 − e − a T z − 1 + k 2 1 − e − b T z − 1 = 1 b − a ( 1 1 − e − a T z − 1 − 1 1 − e − b T z − 1 ) = 1 b − a ( z z − e − a T − z z − e − b T ) begin{aligned} E(z)&=frac{k_1}{1-{rm e}^{-aT}z^{-1}}+frac{k_2}{1-{rm e}^{-bT}z^{-1}}=frac{1}{b-a}left(frac{1}{1-{rm e}^{-aT}z^{-1}}-frac{1}{1-{rm e}^{-bT}z^{-1}}right)\\ &=frac{1}{b-a}left(frac{z}{z-{rm e}^{-aT}}-frac{z}{z-{rm e}^{-bT}}right) end{aligned} E(z)=1−e−aTz−1k1+1−e−bTz−1k2=b−a1(1−e−aTz−11−1−e−bTz−11)=b−a1(z−e−aTz−z−e−bTz)
Example 7.2
求下列函数的 z z z变换。
- e ( t ) = 1 + e − 2 t e(t)=1+{rm e}^{-2t} e(t)=1+e−2t;
- e ( t ) = e − a t sin ω t e(t)={rm e}^{-at}sinomega{t} e(t)=e−atsinωt;
- E ( s ) = 1 s ( s + 1 ) ( s + 2 ) E(s)=displaystylefrac{1}{s(s+1)(s+2)} E(s)=s(s+1)(s+2)1;
解:
-
e ( t ) = 1 + e − 2 t e(t)=1+{rm e}^{-2t} e(t)=1+e−2t;
E ( z ) = Z [ 1 + e − 2 t ] = Z [ 1 ] + Z [ e − 2 t ] E(z)=Z[1+{rm e}^{-2t}]=Z[1]+Z[{rm e}^{-2t}] E(z)=Z[1+e−2t]=Z[1]+Z[e−2t]
其中:
Z [ 1 ( t ) ] = ∑ n = 0 ∞ z − n = z z − 1 , Z [ e − 2 t ] = ∑ n = 0 ∞ e − 2 n T z − n = z z − e − 2 T Z[1(t)]=sum_{n=0}^{infty}z^{-n}=frac{z}{z-1},Z[{rm e}^{-2t}]=sum_{n=0}^{infty}{rm e}^{-2nT}z^{-n}=frac{z}{z-{rm e}^{-2T}} Z[1(t)]=n=0∑∞z−n=z−1z,Z[e−2t]=n=0∑∞e−2nTz−n=z−e−2Tz
则有:
E ( z ) = z z − 1 + z z − e − 2 T = z ( 2 z − 1 − e − 2 T ) z 2 − ( 1 + e − 2 T ) z + e − 2 T E(z)=frac{z}{z-1}+frac{z}{z-{rm e}^{-2T}}=frac{z(2z-1-{rm e}^{-2T})}{z^2-(1+{rm e}^{-2T})z+{rm e}^{-2T}} E(z)=z−1z+z−e−2Tz=z2−(1+e−2T)z+e−2Tz(2z−1−e−2T) -
e ( t ) = e − a t sin ω t e(t)={rm e}^{-at}sinomega{t} e(t)=e−atsinωt;
令 e ( t ) = sin ω t e(t)=sinomega{t} e(t)=sinωt,则有:
E ( z ) = Z [ sin ω t ] = Z [ e j ω t − e − j ω t 2 j ] = ∑ n = 0 ∞ e j ω n T − e − j ω n T 2 j = 1 2 j ( 1 1 − e j ω T z − 1 − 1 1 − e − j ω T z − 1 ) = 1 2 j [ ( e j ω T − e − j ω T ) z − 1 1 − ( e j ω T + e − j ω T ) z − 1 + z − 2 ] = z sin ω T z 2 − 2 z cos ω T + 1 begin{aligned} E(z)&=Z[sinomega{t}]=Zleft[frac{{rm e}^{{rm j}omega{t}}-{rm e^{-{rm j}omega{t}}}}{2{rm j}}right]=sum_{n=0}^{infty}frac{{rm e}^{{rm j}omega{nT}}-{rm e}^{-{rm j}omega{nT}}}{2{rm j}}\\ &=frac{1}{2{rm j}}left(frac{1}{1-{rm e}^{{rm j}omega{T}}z^{-1}}-frac{1}{1-{rm e}^{-{rm j}omega{T}}z^{-1}}right)=frac{1}{2{rm j}}left[frac{({rm e}^{{rm j}omega{T}}-{rm e}^{-{rm j}omega{T}})z^{-1}}{1-({rm e}^{{rm j}omega{T}}+{rm e}^{-{rm j}omega{T}})z^{-1}+z^{-2}}right]\\ &=frac{zsinomega{T}}{z^2-2zcosomega{T}+1} end{aligned} E(z)=Z[sinωt]=Z[2jejωt−e−jωt]=n=0∑∞2jejωnT−e−jωnT=2j1(1−ejωTz−11−1−e−jωTz−11)=2j1[1−(ejωT+e−jωT)z−1+z−2(ejωT−e−jωT)z−1]=z2−2zcosωT+1zsinωT
根据复数位移定理可得:
Z [ e − a t sin ω t ] = E ( z e a T ) = z e a T sin ω T z 2 e 2 a T − 2 z e a T cos ω T + 1 Z[{rm e}^{-at}sinomega{t}]=E(z{rm e}^{aT})=frac{z{rm e}^{aT}sinomega{T}}{z^2{rm e}^{2aT}-2z{rm e}^{aT}cosomega{T}+1} Z[e−atsinωt]=E(zeaT)=z2e2aT−2zeaTcosωT+1zeaTsinωT -
E ( s ) = 1 s ( s + 1 ) ( s + 2 ) E(s)=displaystylefrac{1}{s(s+1)(s+2)} E(s)=s(s+1)(s+2)1;
将 E ( s ) E(s) E(s)展成部分分式:
E ( s ) = 1 2 s − 1 s + 1 + 1 2 ( s + 2 ) E(s)=frac{1}{2s}-frac{1}{s+1}+frac{1}{2(s+2)} E(s)=2s1−s+11+2(s+2)1
对上式逐项进行拉普拉斯反变换,可得:
e ( t ) = 1 2 − e − t + 1 2 e − 2 t e(t)=frac{1}{2}-{rm e}^{-t}+frac{1}{2}{rm e}^{-2t} e(t)=21−e−t+21e−2t
则有:
E ( z ) = Z [ 1 2 ⋅ 1 ( t ) ] − Z [ e − t ] + Z [ 1 2 e − 2 t ] = 1 2 ( z z − 1 − 2 z z − e − T + z z − e − 2 T ) = ( 1 − 2 e − T + e − 2 T ) z 2 2 ( z − 1 ) ( z − e − T ) ( z − e − 2 T ) begin{aligned} E(z)&=Zleft[frac{1}{2}·1(t)right]-Z[{rm e}^{-t}]+Zleft[frac{1}{2}{rm e}^{-2t}right]\\ &=frac{1}{2}left(frac{z}{z-1}-frac{2z}{z-{rm e}^{-T}}+frac{z}{z-{rm e}^{-2T}}right)=frac{(1-2{rm e}^{-T}+{rm e}^{-2T})z^2}{2(z-1)(z-{rm e}^{-T})(z-{rm e}^{-2T})} end{aligned} E(z)=Z[21⋅1(t)]−Z[e−t]+Z[21e−2t]=21(z−1z−z−e−T2z+z−e−2Tz)=2(z−1)(z−e−T)(z−e−2T)(1−2e−T+e−2T)z2
Example 7.3
求下列函数的 z z z反变换。
- E ( z ) = 2 z ( z 2 − 1 ) ( z 2 + 1 ) 2 E(z)=displaystylefrac{2z(z^2-1)}{(z^2+1)^2} E(z)=(z2+1)22z(z2−1);
- E ( z ) = 2 z 2 ( z + 1 ) 2 ( z + 2 ) E(z)=displaystylefrac{2z^2}{(z+1)^2(z+2)} E(z)=(z+1)2(z+2)2z2;
- E ( z ) = z ( z − e − a T ) ( z − e − b T ) E(z)=displaystylefrac{z}{(z-{rm e}^{-aT})(z-{rm e}^{-bT})} E(z)=(z−e−aT)(z−e−bT)z;
解:
-
E ( z ) = 2 z ( z 2 − 1 ) ( z 2 + 1 ) 2 E(z)=displaystylefrac{2z(z^2-1)}{(z^2+1)^2} E(z)=(z2+1)22z(z2−1);
【幂级数法】
E ( z ) = 2 z ( z 2 − 1 ) ( z 2 + 1 ) 2 = 2 z 3 − 2 z z 4 + 2 z 2 + 1 = 2 z − 1 − 2 z − 3 1 + 2 z − 2 + z − 4 = 2 z − 1 − 6 z − 3 + 10 z − 5 − 14 z − 7 + ⋯ + begin{aligned} E(z)&=frac{2z(z^2-1)}{(z^2+1)^2}=frac{2z^3-2z}{z^4+2z^2+1}\\ &=frac{2z^{-1}-2z^{-3}}{1+2z^{-2}+z^{-4}}=2z^{-1}-6z^{-3}+10z^{-5}-14z^{-7}+cdots+ end{aligned} E(z)=(z2+1)22z(z2−1)=z4+2z2+12z3−2z=1+2z−2+z−42z−1−2z−3=2z−1−6z−3+10z−5−14z−7+⋯+
则采样函数为:
e ∗ ( t ) = 2 δ ( t − T ) − 6 δ ( t − 3 T ) + 10 δ ( t − 5 T ) − 14 δ ( t − 7 T ) + ⋯ e^*(t)=2delta(t-T)-6delta(t-3T)+10delta(t-5T)-14delta(t-7T)+cdots e∗(t)=2δ(t−T)−6δ(t−3T)+10δ(t−5T)−14δ(t−7T)+⋯ -
E ( z ) = 2 z 2 ( z + 1 ) 2 ( z + 2 ) E(z)=displaystylefrac{2z^2}{(z+1)^2(z+2)} E(z)=(z+1)2(z+2)2z2;
【反演积分法】
E ( z ) z n − 1 = 2 z n + 1 ( z + 1 ) 2 ( z + 2 ) E(z)z^{n-1}=frac{2z^{n+1}}{(z+1)^2(z+2)} E(z)zn−1=(z+1)2(z+2)2zn+1
有: z 1 = z 2 = − 1 , z 3 = − 2 z_1=z_2=-1,z_3=-2 z1=z2=−1,z3=−2三个极点,则有:
R e s [ 2 z n + 1 ( z + 1 ) 2 ( z + 2 ) ] z → − 1 = lim z → − 1 d d z [ ( z + 1 ) 2 2 z n + 1 ( z + 1 ) 2 ( z + 2 ) ] = lim z → − 1 [ 2 ( n + 1 ) z n ( z + 2 ) − 2 z n + 1 ( z + 2 ) 2 ] = ( 2 n + 4 ) ( − 1 ) n R e s [ 2 z n + 1 ( z + 1 ) 2 ( z + 2 ) ] z → − 1 = lim z → − 2 [ ( z + 2 ) 2 z n + 1 ( z + 1 ) 2 ( z + 2 ) ] = − ( − 1 ) n 2 n + 2 begin{aligned} {rm Res}left[frac{2z^{n+1}}{(z+1)^2(z+2)}right]_{zto-1}&=lim_{zto-1}frac{{rm d}}{{rm d}z}left[(z+1)^2frac{2z^{n+1}}{(z+1)^2(z+2)}right]\\ &=lim_{zto-1}left[frac{2(n+1)z^n(z+2)-2z^{n+1}}{(z+2)^2}right]=(2n+4)(-1)^n\\ {rm Res}left[frac{2z^{n+1}}{(z+1)^2(z+2)}right]_{zto-1}&=lim_{zto-2}left[(z+2)frac{2z^{n+1}}{(z+1)^2(z+2)}right]=-(-1)^n2^{n+2} end{aligned} Res[(z+1)2(z+2)2zn+1]z→−1Res[(z+1)2(z+2)2zn+1]z→−1=z→−1limdzd[(z+1)2(z+1)2(z+2)2zn+1]=z→−1lim[(z+2)22(n+1)zn(z+2)−2zn+1]=(2n+4)(−1)n=z→−2lim[(z+2)(z+1)2(z+2)2zn+1]=−(−1)n2n+2
可得:
e ( n T ) = ( − 1 ) n ( 2 n + 4 − 2 n + 2 ) e(nT)=(-1)^n(2n+4-2^{n+2}) e(nT)=(−1)n(2n+4−2n+2)
采样函数为:
e ∗ ( t ) = ∑ n = 0 ∞ e ( n T ) δ ( t − n T ) = ∑ n = 0 ∞ [ ( − 1 ) n ( 2 n + 4 − 2 n + 2 ) ] δ ( t − n T ) = 2 δ ( t − T ) − 8 δ ( t − 2 T ) + 22 δ ( t − 3 T ) + ⋯ begin{aligned} e^*(t)&=sum_{n=0}^{infty}e(nT)delta(t-nT)=sum_{n=0}^{infty}[(-1)^n(2n+4-2^{n+2})]delta(t-nT)\\ &=2delta(t-T)-8delta(t-2T)+22delta(t-3T)+cdots end{aligned} e∗(t)=n=0∑∞e(nT)δ(t−nT)=n=0∑∞[(−1)n(2n+4−2n+2)]δ(t−nT)=2δ(t−T)−8δ(t−2T)+22δ(t−3T)+⋯ -
E ( z ) = z ( z − e − a T ) ( z − e − b T ) E(z)=displaystylefrac{z}{(z-{rm e}^{-aT})(z-{rm e}^{-bT})} E(z)=(z−e−aT)(z−e−bT)z;
【查表法】
因为
E ( z ) z = 1 ( z − e − a T ) ( z − e − b T ) = 1 e − a T − e − b T [ 1 z − e − a T − 1 z − e − b T ] frac{E(z)}{z}=frac{1}{(z-{rm e}^{-aT})(z-{rm e}^{-bT})}=frac{1}{{rm e}^{-aT}-{rm e}^{-bT}}left[frac{1}{z-{rm e}^{-aT}}-frac{1}{z-{rm e}^{-bT}}right] zE(z)=(z−e−aT)(z−e−bT)1=e−aT−e−bT1[z−e−aT1−z−e−bT1]
有
E ( z ) = 1 e − a T − e − b T [ z z − e − a T − z z − e − b T ] E(z)=frac{1}{{rm e}^{-aT}-{rm e}^{-bT}}left[frac{z}{z-{rm e}^{-aT}}-frac{z}{z-{rm e}^{-bT}}right] E(z)=e−aT−e−bT1[z−e−aTz−z−e−bTz]
由 z z z变换表可知:
e ( n T ) = 1 e − a T − e − b T ( e − a n T − e − b n T ) e(nT)=frac{1}{{rm e}^{-aT}-{rm e}^{-bT}}({rm e}^{-anT}-{rm e}^{-bnT}) e(nT)=e−aT−e−bT1(e−anT−e−bnT)
则有
e ∗ ( t ) = ∑ n = 0 ∞ e − a n T − e − b n T e − a T − e − b T δ ( t − n T ) e^*(t)=sum_{n=0}^{infty}frac{{rm e}^{-anT}-{rm e}^{-bnT}}{{rm e}^{-aT}-{rm e}^{-bT}}delta(t-nT) e∗(t)=n=0∑∞e−aT−e−bTe−anT−e−bnTδ(t−nT)
Example 7.4
求下列 E ( z ) E(z) E(z)的脉冲序列 e ∗ ( t ) e^*(t) e∗(t):
- E ( z ) = z 2 ( z e − 1 ) 2 E(z)=displaystylefrac{z^2}{(z{rm e}-1)^2} E(z)=(ze−1)2z2;
- E ( z ) = 10 z ( z + 1 ) ( z − 1 ) ( z 2 + z + 1 ) E(z)=displaystylefrac{10z(z+1)}{(z-1)(z^2+z+1)} E(z)=(z−1)(z2+z+1)10z(z+1);
解:
-
E ( z ) = z 2 ( z e − 1 ) 2 E(z)=displaystylefrac{z^2}{(z{rm e}-1)^2} E(z)=(ze−1)2z2;
【反演积分法】
e ( n T ) = R e s [ E ( z ) z n − 1 ] z → e − 1 = 1 1 ! lim z → e − 1 d d z [ e − 2 ( z − e − 1 ) 2 z n + 1 ( z − e − 1 ) 2 ] = e − 2 ( n + 1 ) e − n e ∗ ( t ) = ∑ n = 0 ∞ e − 2 [ ( n + 1 ) e − n ] δ ( t − n T ) = e − 2 + 2 e − 3 z − 1 + 3 e − 4 z − 2 + 4 e − 5 z − 3 + ⋯ begin{aligned} &e(nT)={rm Res}[E(z)z^{n-1}]_{zto{rm e}^{-1}}=frac{1}{1!}lim_{zto{rm e}^{-1}}frac{{rm d}}{{rm d}z}left[frac{{rm e}^{-2}(z-{rm e}^{-1})^2z^{n+1}}{(z-{rm e}^{-1})^2}right]={rm e}^{-2}(n+1){rm e}^{-n}\\ &e^*(t)=sum_{n=0}^{infty}{rm e}^{-2}[(n+1){rm e}^{-n}]delta(t-nT)={rm e}^{-2}+2{rm e}^{-3}z^{-1}+3{rm e}^{-4}z^{-2}+4{rm e}^{-5}z^{-3}+cdots end{aligned} e(nT)=Res[E(z)zn−1]z→e−1=1!1z→e−1limdzd[(z−e−1)2e−2(z−e−1)2zn+1]=e−2(n+1)e−ne∗(t)=n=0∑∞e−2[(n+1)e−n]δ(t−nT)=e−2+2e−3z−1+3e−4z−2+4e−5z−3+⋯ -
E ( z ) = 10 z ( z + 1 ) ( z − 1 ) ( z 2 + z + 1 ) E(z)=displaystylefrac{10z(z+1)}{(z-1)(z^2+z+1)} E(z)=(z−1)(z2+z+1)10z(z+1);
【幂级数法】
E ( z ) = 10 z 2 + 10 z z 3 − 1 = 10 ( z − 1 + z − 2 + z − 4 + z − 5 + z − 7 + ⋯ ) E(z)=frac{10z^2+10z}{z^3-1}=10(z^{-1}+z^{-2}+z^{-4}+z^{-5}+z^{-7}+cdots) E(z)=z3−110z2+10z=10(z−1+z−2+z−4+z−5+z−7+⋯)
则有
e ∗ ( t ) = 10 [ δ ( t − T ) + δ ( t − 2 T ) + δ ( t − 4 T ) + δ ( t − 5 T ) + δ ( t − 7 T ) + ⋯ ] e^*(t)=10[delta(t-T)+delta(t-2T)+delta(t-4T)+delta(t-5T)+delta(t-7T)+cdots] e∗(t)=10[δ(t−T)+δ(t−2T)+δ(t−4T)+δ(t−5T)+δ(t−7T)+⋯]
Example 7.5
求 E ( s ) = 1 − e − s s 2 ( s + 1 ) E(s)=displaystylefrac{1-{rm e}^{-s}}{s^2(s+1)} E(s)=s2(s+1)1−e−s的 z z z变换.
解:
将
E
(
s
)
E(s)
E(s)展成部分分式,有:
E
(
s
)
=
1
−
e
−
s
s
2
(
s
+
1
)
=
(
1
s
2
−
1
s
+
1
s
+
1
)
−
(
1
s
2
−
1
s
+
1
s
+
1
)
e
−
T
s
E(s)=frac{1-{rm e}^{-s}}{s^2(s+1)}=left(frac{1}{s^2}-frac{1}{s}+frac{1}{s+1}right)-left(frac{1}{s^2}-frac{1}{s}+frac{1}{s+1}right){rm e}^{-Ts}
E(s)=s2(s+1)1−e−s=(s21−s1+s+11)−(s21−s1+s+11)e−Ts
对上式进行
z
z
z变换:
Z
[
1
s
2
−
1
s
+
1
s
+
1
]
=
T
z
(
z
−
1
)
2
−
z
z
−
1
+
z
z
−
e
−
T
Z
[
(
1
s
2
−
1
s
+
1
s
+
1
)
e
−
T
s
]
=
(
T
z
(
z
−
1
)
2
−
z
z
−
1
+
z
z
−
e
−
T
)
z
−
1
begin{aligned} &Zleft[frac{1}{s^2}-frac{1}{s}+frac{1}{s+1}right]=frac{Tz}{(z-1)^2}-frac{z}{z-1}+frac{z}{z-{rm e}^{-T}}\\ &Zleft[left(frac{1}{s^2}-frac{1}{s}+frac{1}{s+1}right){rm e}^{-Ts}right]=left(frac{Tz}{(z-1)^2}-frac{z}{z-1}+frac{z}{z-{rm e}^{-T}}right)z^{-1} end{aligned}
Z[s21−s1+s+11]=(z−1)2Tz−z−1z+z−e−TzZ[(s21−s1+s+11)e−Ts]=((z−1)2Tz−z−1z+z−e−Tz)z−1
有
E
(
z
)
=
(
1
−
z
−
1
)
(
T
z
(
z
−
1
)
2
−
z
z
−
1
+
z
z
−
e
−
T
)
=
T
z
−
1
−
1
+
z
−
1
z
−
e
−
T
=
1
−
(
T
+
1
)
e
−
T
+
(
T
−
1
+
e
−
T
)
z
(
z
−
1
)
(
z
−
e
−
T
)
=
1
−
(
T
+
1
)
e
−
T
+
(
T
−
1
+
e
−
T
)
z
z
2
−
(
1
+
e
−
T
)
z
+
e
−
T
begin{aligned} E(z)&=(1-z^{-1})left(frac{Tz}{(z-1)^2}-frac{z}{z-1}+frac{z}{z-{rm e}^{-T}}right)\\ &=frac{T}{z-1}-1+frac{z-1}{z-{rm e}^{-T}}=frac{1-(T+1){rm e}^{-T}+(T-1+{rm e}^{-T})z}{(z-1)(z-{rm e}^{-T})}\\ &=frac{1-(T+1){rm e}^{-T}+(T-1+{rm e}^{-T})z}{z^2-(1+{rm e}^{-T})z+{rm e}^{-T}} end{aligned}
E(z)=(1−z−1)((z−1)2Tz−z−1z+z−e−Tz)=z−1T−1+z−e−Tz−1=(z−1)(z−e−T)1−(T+1)e−T+(T−1+e−T)z=z2−(1+e−T)z+e−T1−(T+1)e−T+(T−1+e−T)z
令
T
=
1
T=1
T=1,有:
E
(
z
)
=
1
−
2
e
−
1
+
e
−
1
z
z
2
−
(
1
+
e
−
1
)
z
+
e
−
1
=
0.368
z
+
0.264
z
2
−
1.368
z
+
0.368
E(z)=frac{1-2{rm e}^{-1}+{rm e}^{-1}z}{z^2-(1+{rm e}^{-1})z+{rm e}^{-1}}=frac{0.368z+0.264}{z^2-1.368z+0.368}
E(z)=z2−(1+e−1)z+e−11−2e−1+e−1z=z2−1.368z+0.3680.368z+0.264
Example 7.6
确定下列函数的初值和终值:
- E ( z ) = z 2 ( z − 0.8 ) ( z − 0.1 ) E(z)=displaystylefrac{z^2}{(z-0.8)(z-0.1)} E(z)=(z−0.8)(z−0.1)z2;
- E ( z ) = T z − 1 ( 1 − z − 1 ) 2 E(z)=displaystylefrac{Tz^{-1}}{(1-z^{-1})^2} E(z)=(1−z−1)2Tz−1;
解:
-
E ( z ) = z 2 ( z − 0.8 ) ( z − 0.1 ) E(z)=displaystylefrac{z^2}{(z-0.8)(z-0.1)} E(z)=(z−0.8)(z−0.1)z2;
由终值定理可得:
e s s ( ∞ ) = lim z → 1 ( 1 − z − 1 ) z 2 ( z − 0.8 ) ( z − 0.1 ) = 0 e_{ss}(infty)=lim_{zto1}(1-z^{-1})displaystylefrac{z^2}{(z-0.8)(z-0.1)}=0 ess(∞)=z→1lim(1−z−1)(z−0.8)(z−0.1)z2=0
由
E ( z ) = z 2 ( z − 0.8 ) ( z − 0.1 ) = 1 1 − 0.9 z − 1 + 0.08 z − 2 = 1 + 0.9 z − 1 + 0.73 z − 2 + ⋯ E(z)=displaystylefrac{z^2}{(z-0.8)(z-0.1)}=frac{1}{1-0.9z^{-1}+0.08z^{-2}}=1+0.9z^{-1}+0.73z^{-2}+cdots E(z)=(z−0.8)(z−0.1)z2=1−0.9z−1+0.08z−21=1+0.9z−1+0.73z−2+⋯
可得:
e ( 0 ) = 1 e(0)=1 e(0)=1 -
E ( z ) = T z − 1 ( 1 − z − 1 ) 2 E(z)=displaystylefrac{Tz^{-1}}{(1-z^{-1})^2} E(z)=(1−z−1)2Tz−1;
由终值定理可得:
e s s ( ∞ ) = lim z → 1 ( 1 − z − 1 ) T z − 1 ( 1 − z − 1 ) 2 = ∞ e_{ss}(infty)=lim_{zto1}(1-z^{-1})displaystylefrac{Tz^{-1}}{(1-z^{-1})^2}=infty ess(∞)=z→1lim(1−z−1)(1−z−1)2Tz−1=∞
由
E ( z ) = T z − 1 ( 1 − z − 1 ) 2 = T z − 1 1 − 2 z − 1 + z − 2 = T z − 1 + 2 T z − 2 + ⋯ E(z)=frac{Tz^{-1}}{(1-z^{-1})^2}=frac{Tz^{-1}}{1-2z^{-1}+z^{-2}}=Tz^{-1}+2Tz^{-2}+cdots E(z)=(1−z−1)2Tz−1=1−2z−1+z−2Tz−1=Tz−1+2Tz−2+⋯
可得:
e ( 0 ) = 0 e(0)=0 e(0)=0
Example 7.7
求解下列差分方程,结果以 c ( n T ) c(nT) c(nT)表示:
- c ∗ ( t + 2 T ) − 3 c ∗ ( t + T ) − 10 c ∗ ( t ) = r ∗ ( t ) , r ( t ) = e 3 t , r ( t ) = 0 , t < 0 c^*(t+2T)-3c^*(t+T)-10c^*(t)=r^*(t),r(t)={rm e}^{3t},r(t)=0,t<0 c∗(t+2T)−3c∗(t+T)−10c∗(t)=r∗(t),r(t)=e3t,r(t)=0,t<0;
- c ( k + 2 ) + 4 c ( k + 1 ) + 3 c ( k ) = 2 k , c ( 0 ) = c ( 1 ) = 0 c(k+2)+4c(k+1)+3c(k)=2k,c(0)=c(1)=0 c(k+2)+4c(k+1)+3c(k)=2k,c(0)=c(1)=0;
解:
-
c ∗ ( t + 2 T ) − 3 c ∗ ( t + T ) − 10 c ∗ ( t ) = r ∗ ( t ) , r ( t ) = e 3 t , r ( t ) = 0 , t < 0 c^*(t+2T)-3c^*(t+T)-10c^*(t)=r^*(t),r(t)={rm e}^{3t},r(t)=0,t<0 c∗(t+2T)−3c∗(t+T)−10c∗(t)=r∗(t),r(t)=e3t,r(t)=0,t<0;
因为
z 2 C ( z ) − 3 z C ( z ) − 10 C ( z ) = R ( z ) = z z − e 3 T z^2C(z)-3zC(z)-10C(z)=R(z)=frac{z}{z-{rm e}^{3T}} z2C(z)−3zC(z)−10C(z)=R(z)=z−e3Tz
有
C ( z ) = z ( z − e 3 T ) ( z 2 − 3 z − 10 ) = z ( z − e 3 T ) ( z − 5 ) ( z + 2 ) C(z)=frac{z}{(z-{rm e}^{3T})(z^2-3z-10)}=frac{z}{(z-{rm e}^{3T})(z-5)(z+2)} C(z)=(z−e3T)(z2−3z−10)z=(z−e3T)(z−5)(z+2)z
用反演积分法,可得:
c ( n T ) = R e s [ C ( z ) ⋅ z n − 1 ] z → e 3 T + R e s [ C ( z ) ⋅ z n − 1 ] z → 5 + R e s [ C ( z ) ⋅ z n − 1 ] z → − 2 = lim z → e 3 T [ ( z − e 3 T ) z n ( z − e 3 T ) ( z − 5 ) ( z + 2 ) ] + lim z → 5 [ ( z − 5 ) z n ( z − e 3 T ) ( z − 5 ) ( z + 2 ) ] + lim z → − 2 [ ( z + 2 ) z n ( z − e 3 T ) ( z − 5 ) ( z + 2 ) ] = e 3 n T ( e 3 T − 5 ) ( e 3 T + 2 ) + 5 n 7 ( 5 − e 3 T ) + ( − 2 ) n 7 ( e 3 T + 2 ) begin{aligned} c(nT)&={rm Res}[C(z)·z^{n-1}]_{zto{rm e}^{3T}}+{rm Res}[C(z)·z^{n-1}]_{zto{rm 5}}+{rm Res}[C(z)·z^{n-1}]_{zto{rm-2}}\\ &=lim_{zto{rm e}^{3T}}left[frac{(z-{rm e}^{3T})z^n}{(z-{rm e}^{3T})(z-5)(z+2)}right]+lim_{zto5}left[frac{(z-5)z^n}{(z-{rm e}^{3T})(z-5)(z+2)}right]\\ &+lim_{zto-2}left[frac{(z+2)z^n}{(z-{rm e}^{3T})(z-5)(z+2)}right]\\ &=frac{{rm e}^{3nT}}{({rm e}^{3T}-5)({rm e}^{3T}+2)}+frac{5^n}{7(5-{rm e}^{3T})}+frac{(-2)^n}{7({rm e}^{3T}+2)} end{aligned} c(nT)=Res[C(z)⋅zn−1]z→e3T+Res[C(z)⋅zn−1]z→5+Res[C(z)⋅zn−1]z→−2=z→e3Tlim[(z−e3T)(z−5)(z+2)(z−e3T)zn]+z→5lim[(z−e3T)(z−5)(z+2)(z−5)zn]+z→−2lim[(z−e3T)(z−5)(z+2)(z+2)zn]=(e3T−5)(e3T+2)e3nT+7(5−e3T)5n+7(e3T+2)(−2)n -
c ( k + 2 ) + 4 c ( k + 1 ) + 3 c ( k ) = 2 k , c ( 0 ) = c ( 1 ) = 0 c(k+2)+4c(k+1)+3c(k)=2k,c(0)=c(1)=0 c(k+2)+4c(k+1)+3c(k)=2k,c(0)=c(1)=0;
因为
z 2 C ( z ) + 4 z C ( z ) + 3 C ( z ) = R ( z ) = 2 T z ( z − 1 ) 2 z^2C(z)+4zC(z)+3C(z)=R(z)=frac{2Tz}{(z-1)^2} z2C(z)+4zC(z)+3C(z)=R(z)=(z−1)22Tz
有
C ( z ) = 2 T z ( z − 1 ) 2 ( z 2 + 4 z + 3 ) = 2 T z ( z + 1 ) ( z + 3 ) ( z − 1 ) 2 C(z)=frac{2Tz}{(z-1)^2(z^2+4z+3)}=frac{2Tz}{(z+1)(z+3)(z-1)^2} C(z)=(z−1)2(z2+4z+3)2Tz=(z+1)(z+3)(z−1)22Tz
用反演积分法,可得:
c ( n T ) = R e s [ C ( z ) ⋅ z n − 1 ] z → − 1 + R e s [ C ( z ) ⋅ z n − 1 ] z → − 3 + R e s [ C ( s ) ⋅ z n − 1 ] z → 1 = lim z → − 1 [ 2 T ( z + 1 ) z n ( z + 1 ) ( z + 3 ) ( z − 1 ) 2 ] + lim z → − 3 [ 2 T ( z + 3 ) z n ( z + 1 ) ( z + 3 ) ( z − 1 ) 2 ] + 1 1 ! lim z → 1 d d z [ 2 T ( z − 1 ) 2 z n ( z + 1 ) ( z + 3 ) ( z − 1 ) 2 ] = n T 4 − ( − 3 ) n T 16 − 3 T 16 + ( − 1 ) n T 4 c ∗ ( t ) = ∑ n = 0 ∞ [ n T 4 − ( − 3 ) n T 16 − 3 T 16 + ( − 1 ) n T 4 ] δ ( t − n T ) = 2 T δ ( t − 3 T ) − 4 T δ ( t − 4 T ) + 16 T δ ( t − 5 T ) + ⋯ begin{aligned} c(nT)&={rm Res}[C(z)·z^{n-1}]_{zto-1}+{rm Res}[C(z)·z^{n-1}]_{zto-3}+{rm Res}[C(s)·z^{n-1}]_{zto1}\\ &=lim_{zto-1}left[frac{2T(z+1)z^n}{(z+1)(z+3)(z-1)^2}right]+lim_{zto-3}left[frac{2T(z+3)z^n}{(z+1)(z+3)(z-1)^2}right]\\ &+frac{1}{1!}lim_{zto1}frac{{rm d}}{{rm d}z}left[frac{2T(z-1)^2z^n}{(z+1)(z+3)(z-1)^2}right]\\ &=frac{nT}{4}-(-3)^nfrac{T}{16}-frac{3T}{16}+(-1)^nfrac{T}{4}\\ c^*(t)&=sum_{n=0}^{infty}left[frac{nT}{4}-(-3)^nfrac{T}{16}-frac{3T}{16}+(-1)^nfrac{T}{4}right]delta(t-nT)\\ &=2Tdelta(t-3T)-4Tdelta(t-4T)+16Tdelta(t-5T)+cdots end{aligned} c(nT)c∗(t)=Res[C(z)⋅zn−1]z→−1+Res[C(z)⋅zn−1]z→−3+Res[C(s)⋅zn−1]z→1=z→−1lim[(z+1)(z+3)(z−1)22T(z+1)zn]+z→−3lim[(z+1)(z+3)(z−1)22T(z+3)zn]+1!1z→1limdzd[(z+1)(z+3)(z−1)22T(z−1)2zn]=4nT−(−3)n16T−163T+(−1)n4T=n=0∑∞[4nT−(−3)n16T−163T+(−1)n4T]δ(t−nT)=2Tδ(t−3T)−4Tδ(t−4T)+16Tδ(t−5T)+⋯
Example 7.8
系统结构图如下所示,求系统的输出
z
z
z变换
C
(
z
)
C(z)
C(z)。
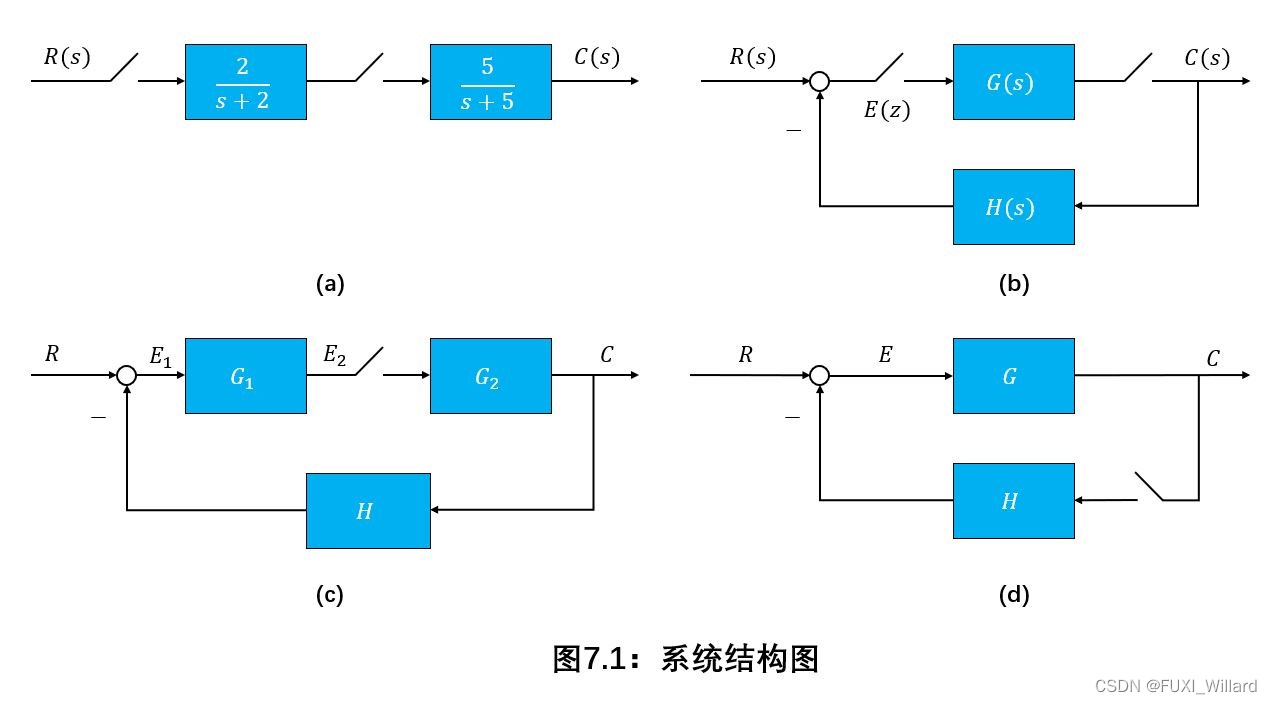
解:
【图a】
G
(
z
)
=
G
1
(
z
)
G
2
(
z
)
=
Z
[
2
s
+
2
]
⋅
Z
[
5
s
+
5
]
=
2
z
z
−
e
−
2
T
⋅
5
z
z
−
e
−
5
T
=
10
z
2
(
z
−
e
−
2
T
)
(
z
−
e
−
5
T
)
begin{aligned} G(z)&=G_1(z)G_2(z)=Zleft[frac{2}{s+2}right]·Zleft[frac{5}{s+5}right]=frac{2z}{z-{rm e}^{-2T}}·frac{5z}{z-{rm e}^{-5T}}\\ &=frac{10z^2}{(z-{rm e}^{-2T})(z-{rm e}^{-5T})} end{aligned}
G(z)=G1(z)G2(z)=Z[s+22]⋅Z[s+55]=z−e−2T2z⋅z−e−5T5z=(z−e−2T)(z−e−5T)10z2
【图b】
由于
C
(
z
)
=
G
(
z
)
E
(
z
)
,
E
(
z
)
=
Z
[
R
(
s
)
−
H
(
s
)
C
(
z
)
]
=
R
(
z
)
−
H
(
z
)
C
(
z
)
C(z)=G(z)E(z),E(z)=Z[R(s)-H(s)C(z)]=R(z)-H(z)C(z)
C(z)=G(z)E(z),E(z)=Z[R(s)−H(s)C(z)]=R(z)−H(z)C(z)
故有
C
(
z
)
=
G
(
z
)
[
R
(
z
)
−
H
(
z
)
C
(
z
)
]
⇒
C
(
z
)
=
G
(
z
)
R
(
z
)
1
+
G
(
z
)
H
(
z
)
C(z)=G(z)[R(z)-H(z)C(z)]Rightarrow{C(z)}=frac{G(z)R(z)}{1+G(z)H(z)}
C(z)=G(z)[R(z)−H(z)C(z)]⇒C(z)=1+G(z)H(z)G(z)R(z)
【图c】
C
(
s
)
=
G
2
(
s
)
E
2
∗
(
s
)
E
2
(
s
)
=
G
1
(
s
)
E
1
(
s
)
=
G
1
(
s
)
[
R
(
s
)
−
H
(
s
)
C
(
s
)
]
=
G
1
(
s
)
[
R
(
s
)
−
H
(
s
)
G
2
(
s
)
E
2
∗
(
s
)
]
E
2
∗
(
s
)
=
G
1
R
∗
(
s
)
1
+
G
1
G
2
H
∗
(
s
)
C
∗
(
s
)
=
G
2
∗
(
s
)
E
2
∗
(
s
)
=
G
2
∗
(
s
)
G
1
R
∗
(
s
)
1
+
G
1
G
2
H
∗
(
s
)
C
(
z
)
=
G
2
(
z
)
G
1
R
(
z
)
1
+
G
1
G
2
H
(
z
)
begin{aligned} C(s)&=G_2(s)E_2^*(s)\\ E_2(s)&=G_1(s)E_1(s)=G_1(s)[R(s)-H(s)C(s)]\\ &=G_1(s)[R(s)-H(s)G_2(s)E_2^*(s)]\\ E_2^*(s)&=frac{G_1R^*(s)}{1+G_1G_2H^*(s)}\\ C^*(s)&=G_2^*(s)E_2^*(s)=frac{G_2^*(s)G_1R^*(s)}{1+G_1G_2H^*(s)}\\ C(z)&=frac{G_2(z)G_1R(z)}{1+G_1G_2H(z)} end{aligned}
C(s)E2(s)E2∗(s)C∗(s)C(z)=G2(s)E2∗(s)=G1(s)E1(s)=G1(s)[R(s)−H(s)C(s)]=G1(s)[R(s)−H(s)G2(s)E2∗(s)]=1+G1G2H∗(s)G1R∗(s)=G2∗(s)E2∗(s)=1+G1G2H∗(s)G2∗(s)G1R∗(s)=1+G1G2H(z)G2(z)G1R(z)
【图d】
C
(
s
)
=
G
(
s
)
E
(
s
)
,
E
(
s
)
=
R
(
s
)
−
H
(
s
)
C
∗
(
s
)
C
(
s
)
=
G
(
s
)
[
R
(
s
)
−
H
(
s
)
C
∗
(
s
)
]
,
C
∗
(
s
)
=
G
R
∗
(
s
)
−
G
H
∗
(
s
)
C
∗
(
s
)
C
∗
(
s
)
=
G
R
∗
(
s
)
1
+
G
H
∗
(
s
)
,
C
(
z
)
=
G
R
(
z
)
1
+
G
H
(
z
)
begin{aligned} C(s)&=G(s)E(s),E(s)=R(s)-H(s)C^*(s)\\ C(s)&=G(s)[R(s)-H(s)C^*(s)],C^*(s)=GR^*(s)-GH^*(s)C^*(s)\\ C^*(s)&=frac{GR^*(s)}{1+GH^*(s)},C(z)=frac{GR(z)}{1+GH(z)} end{aligned}
C(s)C(s)C∗(s)=G(s)E(s),E(s)=R(s)−H(s)C∗(s)=G(s)[R(s)−H(s)C∗(s)],C∗(s)=GR∗(s)−GH∗(s)C∗(s)=1+GH∗(s)GR∗(s),C(z)=1+GH(z)GR(z)
Example 7.9
采样系统结构图如下所示,求开环脉冲传递函数
G
(
z
)
G(z)
G(z)和闭环脉冲传递函数
Φ
(
z
)
Phi(z)
Φ(z).
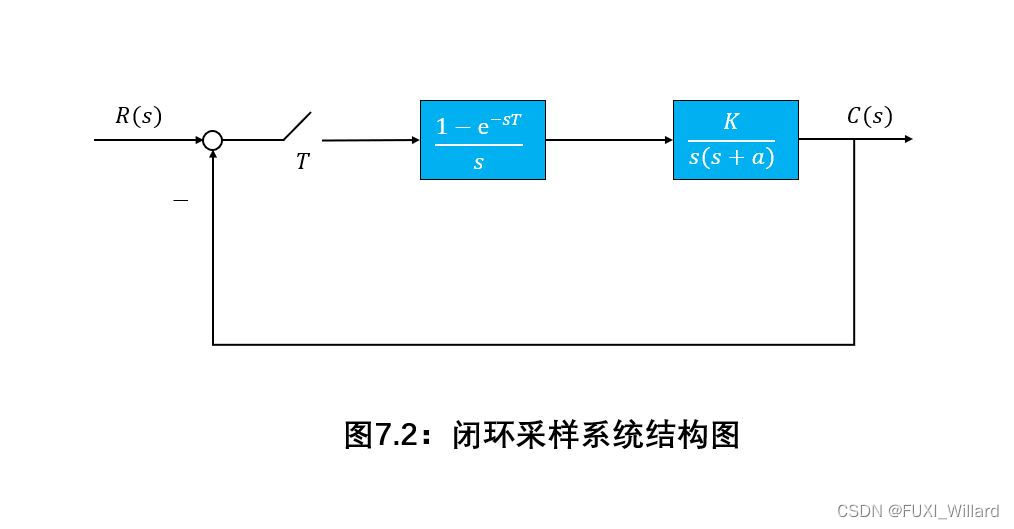
解:
开环脉冲传递函数:
G
(
z
)
=
Z
[
(
1
−
e
−
s
T
)
K
s
2
(
s
+
a
)
]
=
(
1
−
z
−
1
)
Z
[
1
s
2
(
s
+
a
)
]
=
(
1
−
z
−
1
)
⋅
1
a
2
Z
[
a
s
2
−
1
s
+
1
s
+
a
]
=
(
1
−
z
−
1
)
⋅
1
a
2
[
a
T
z
(
z
−
1
)
2
−
z
z
−
1
+
z
z
−
e
−
a
T
]
=
(
a
T
+
e
−
a
T
−
1
)
z
+
1
−
(
a
T
+
1
)
e
−
a
T
a
2
(
z
−
1
)
(
z
−
e
−
a
T
)
begin{aligned} G(z)&=Zleft[frac{(1-{rm e}^{-sT})K}{s^2(s+a)}right]=(1-z^{-1})Zleft[frac{1}{s^2(s+a)}right] =(1-z^{-1})·frac{1}{a^2}Zleft[frac{a}{s^2}-frac{1}{s}+frac{1}{s+a}right]\\ &=(1-z^{-1})·frac{1}{a^2}left[frac{aTz}{(z-1)^2}-frac{z}{z-1}+frac{z}{z-{rm e}^{-aT}}right] =frac{(aT+{rm e}^{-aT}-1)z+1-(aT+1){rm e}^{-aT}}{a^2(z-1)(z-{rm e}^{-aT})} end{aligned}
G(z)=Z[s2(s+a)(1−e−sT)K]=(1−z−1)Z[s2(s+a)1]=(1−z−1)⋅a21Z[s2a−s1+s+a1]=(1−z−1)⋅a21[(z−1)2aTz−z−1z+z−e−aTz]=a2(z−1)(z−e−aT)(aT+e−aT−1)z+1−(aT+1)e−aT
闭环脉冲传递函数为:
Φ
(
z
)
=
G
(
z
)
1
+
G
(
z
)
=
(
a
T
+
e
−
a
T
−
1
)
z
+
1
−
(
a
T
+
1
)
e
−
a
T
a
2
z
2
+
(
a
T
−
a
2
−
a
2
e
−
a
T
+
e
−
a
T
−
1
)
z
+
1
+
(
a
2
−
a
T
−
1
)
e
−
a
T
Phi(z)=frac{G(z)}{1+G(z)}=frac{(aT+{rm e}^{-aT}-1)z+1-(aT+1){rm e}^{-aT}}{a^2z^2+(aT-a^2-a^2{rm e}^{-aT}+{rm e}^{-aT}-1)z+1+(a^2-aT-1){rm e}^{-aT}}
Φ(z)=1+G(z)G(z)=a2z2+(aT−a2−a2e−aT+e−aT−1)z+1+(a2−aT−1)e−aT(aT+e−aT−1)z+1−(aT+1)e−aT
Example 7.10
已知采样系统结构图如下图所示,判断系统的稳定性.
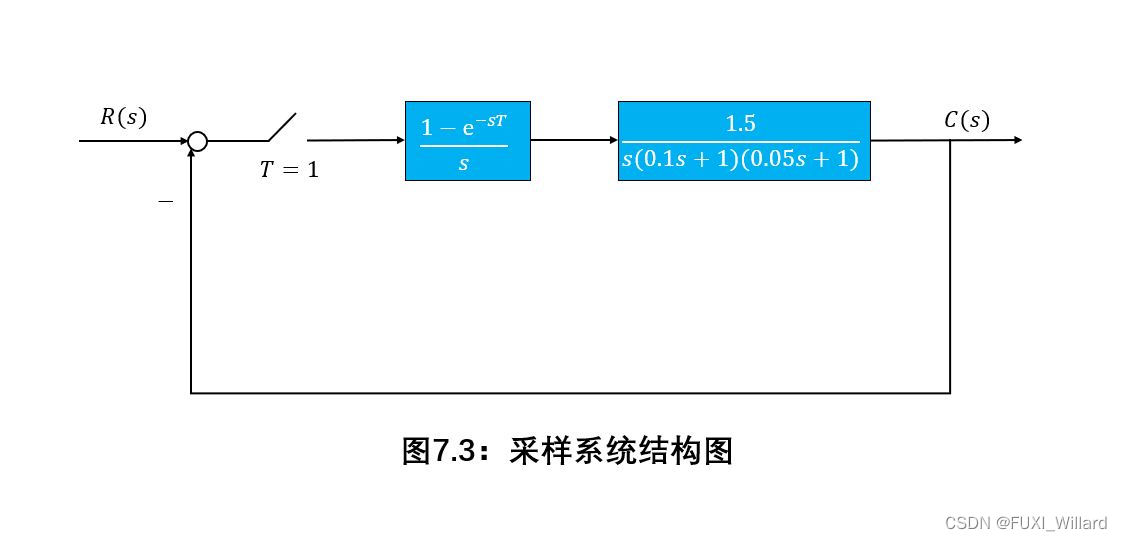
解:
系统开环脉冲传递函数为:
G
h
G
0
(
z
)
=
Z
[
1
−
e
−
T
s
s
⋅
1.5
s
(
0.1
s
+
1
)
(
0.05
s
+
1
)
]
=
(
1
−
z
−
1
)
Z
[
1.5
s
2
(
0.1
s
+
1
)
(
0.05
s
+
1
)
]
=
1.5
(
1
−
z
−
1
)
Z
[
−
0.15
s
+
0.2
s
+
10
−
0.05
s
+
20
+
1
s
2
]
=
1.5
(
1
−
z
−
1
)
[
−
0.15
z
−
1
+
0.2
z
z
−
e
−
10
−
0.05
z
z
−
e
−
20
+
z
(
z
−
1
)
2
]
=
1.275
z
+
0.225
z
2
−
z
begin{aligned} G_hG_0(z)&=Zleft[frac{1-{rm e}^{-Ts}}{s}·frac{1.5}{s(0.1s+1)(0.05s+1)}right]=(1-z^{-1})Zleft[frac{1.5}{s^2(0.1s+1)(0.05s+1)}right]\\ &=1.5(1-z^{-1})Zleft[-frac{0.15}{s}+frac{0.2}{s+10}-frac{0.05}{s+20}+frac{1}{s^2}right]\\ &=1.5(1-z^{-1})left[-frac{0.15}{z-1}+frac{0.2z}{z-{rm e}^{-10}}-frac{0.05z}{z-{rm e}^{-20}}+frac{z}{(z-1)^2}right]\\ &=frac{1.275z+0.225}{z^2-z} end{aligned}
GhG0(z)=Z[s1−e−Ts⋅s(0.1s+1)(0.05s+1)1.5]=(1−z−1)Z[s2(0.1s+1)(0.05s+1)1.5]=1.5(1−z−1)Z[−s0.15+s+100.2−s+200.05+s21]=1.5(1−z−1)[−z−10.15+z−e−100.2z−z−e−200.05z+(z−1)2z]=z2−z1.275z+0.225
闭环脉冲传递函数为:
Φ
(
z
)
=
G
h
G
0
(
z
)
1
+
G
h
G
0
(
z
)
=
1.275
z
+
0.225
z
2
+
0.275
z
+
0.225
Phi(z)=frac{G_hG_0(z)}{1+G_hG_0(z)}=frac{1.275z+0.225}{z^2+0.275z+0.225}
Φ(z)=1+GhG0(z)GhG0(z)=z2+0.275z+0.2251.275z+0.225
闭环特征方程为:
D
(
z
)
=
z
2
+
0.275
z
+
0.225
=
0
⇒
z
1
,
2
=
−
0.1375
±
0.454
j
D(z)=z^2+0.275z+0.225=0Rightarrow{z_{1,2}}=-0.1375±0.454{rm j}
D(z)=z2+0.275z+0.225=0⇒z1,2=−0.1375±0.454j
系统的特征根全部位于单位圆内,故离散系统是稳定的.
【系统单位阶跃响应】
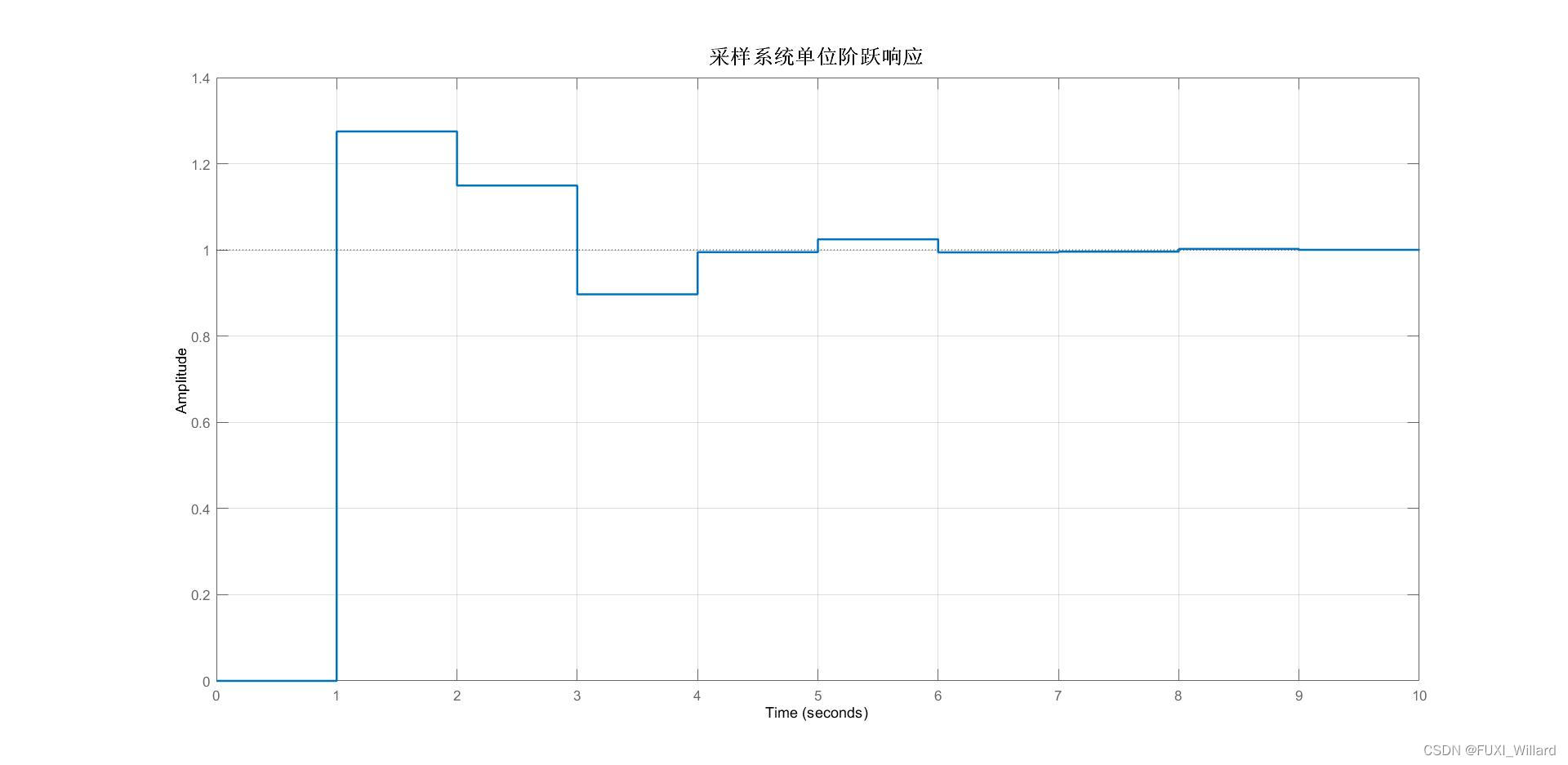
最后
以上就是勤恳蓝天最近收集整理的关于Chapter7.1:线性离散系统的分析与校正的全部内容,更多相关Chapter7.1:线性离散系统内容请搜索靠谱客的其他文章。








发表评论 取消回复