MOOS-ivp 实验六 海洋声学环境

第六个实验主要内容是对于海洋声学环境的一个详细讲解，其中涉及到了一些公式和图片，我尽量在自己理解的基础上写的简单易懂一些。

前言

本章最主要的内容：
（1）海洋声波波导 Ocean Acoustic Waveguide
（2）光线追踪 Ray Tracing
（3）声压 Acoustic Pressure
（4）线性声速剖面 Linear Sound Speed Profile

一、海洋声学环境

1.海洋声波导

海洋是一个声波波导，声音在传播过程中，上面受到海面限制，下面受到海底限制。类似于光的折射率，声波波导在声速传播过程中有着相同的作用。在海洋里，声速和温度、盐度、密度、静压有关。海洋里，声速是温度、盐度和压力的函数，而压力又是深度的函数。总的来说，在海洋深处，盐度和温度都近似保持不变。在海水表面，由于太阳照射蒸发水分以及淡水河流的涌入，海水表面的温度和盐度是一个不断变化的状态。但是海水的深度仍旧是最主要的因素，所以对于绝大部分的应用场合来说，可以假设水平面上声速与周围环境无关。
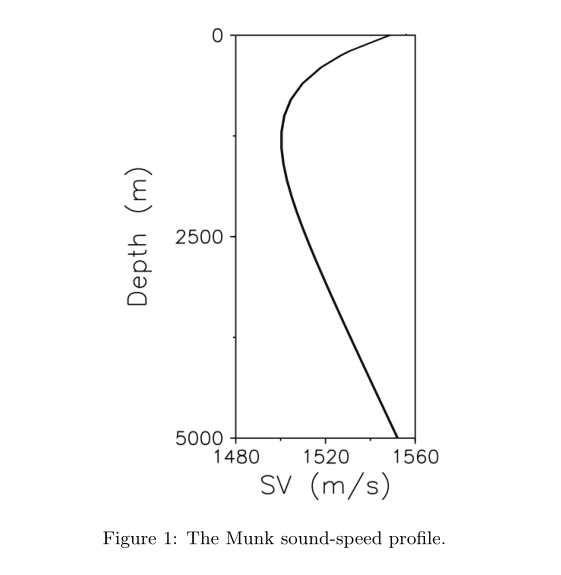
munk剖面是一种理想化的声速剖面，这个剖面中声速的主要变化因素与深度相关，我们可以通过munk剖面了解到许多声速的典型特征，下面给出munk剖面的公式：

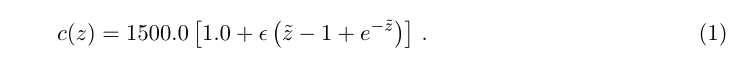
其中常数=
比例深度：

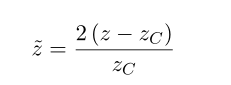
在上面的式子中Zc我们通常称作是最小声速时的深度，又被叫做 SOF AR Channel depth。其大概范围一般在1000-1500米深。在图（1）中的Zc大概是1300m/s。

2.光线追踪

类似于光学，声音在根据深度变化的介质中传播时，也有斯涅耳定律：

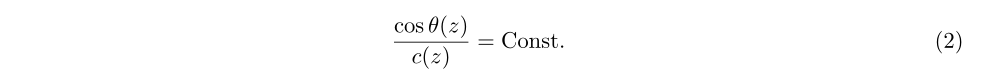
其中的$\theta (z)$是在$z$深度下的光线和水平线的夹角，称作grazing angle。与深度成线性的声速，在温度和盐度不变的情况下，就会产生如下类似于圆形截面的路径。

对于一般的声速变化，射线追踪是通过对常微分方程的解耦来实现的。
在圆柱坐标$(r,z)$中，射线方程如下:
$$\begin{gathered} \frac{\mathrm{d}r}{\mathrm{d}s}=c\xi (s),\frac{\mathrm{d}\xi }{\mathrm{d}s}=-\frac{1}{c^2}\frac{\mathrm{d}c}{\mathrm{d}r} \\ \frac{\mathrm{d}z}{\mathrm{d}s}=c\xi (s),\frac{\mathrm{d}\zeta }{\mathrm{d}s}=-\frac{1}{c^2}\frac{\mathrm{d}c}{\mathrm{d}z} \end{gathered}$$
其中$[r(s),z(s)]$是距离-深度平面中光线的轨迹，$s$是弧长，具体显示在图2中。

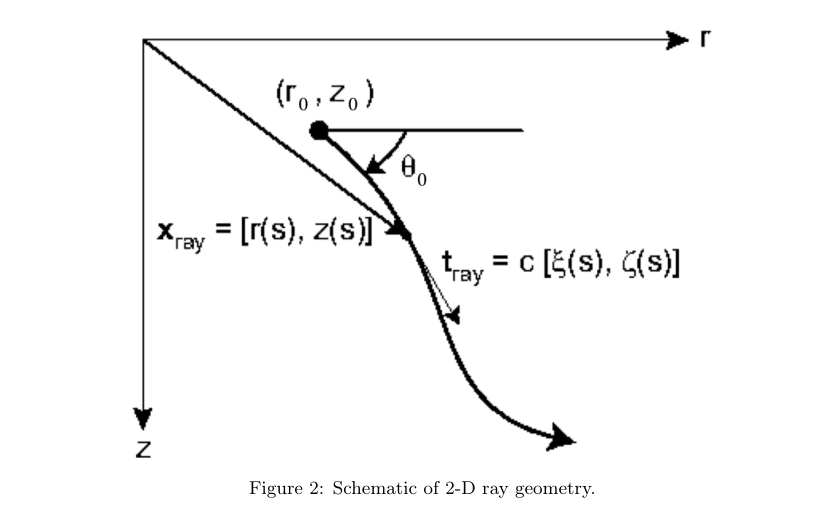
在这里，我们假设声速分布与范围没有关系$dc/dr=0$。为了以一阶形式书写方程，引入辅助变量$\xi (s)$和$\zeta (s)$。回想一下，曲线的切向量$[r(s),z(s)]$由$[dr/ds,dr/dz]$给出。因此从上述的方程来看光线的切向量是$c[\xi (s)$,$\zeta (s)]$。
这组常微分方程的求解可以用欧拉方式或者龙格库塔法来进行求解。为了完善射线方程，还需要初始条件，如图2所示，初始状态就是光线从起始位置$(r_0,z_0)$以指定的起始角${\theta }_0$发射，所以有方程:

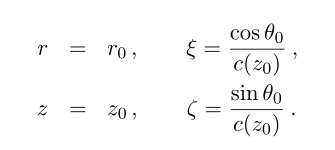
初始坐标是一个给定的量，但是起始角是一个未知的变量。

3.声压

沿着每条射线的压力场振幅是：

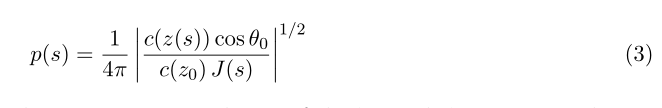
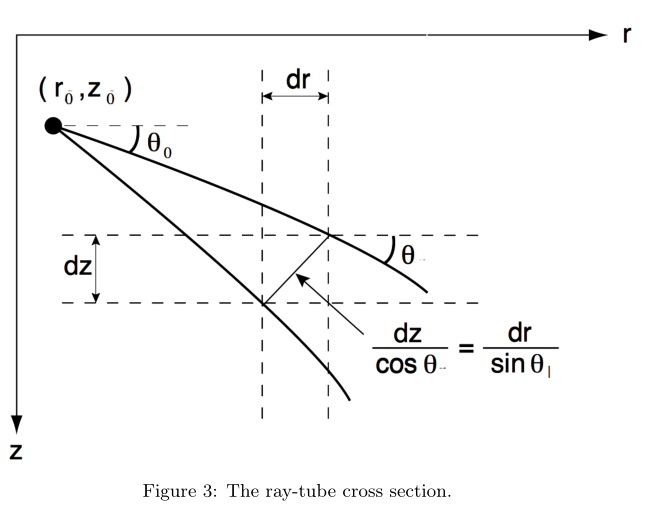
其中$J(s)$是射线管相对横截面积的一个度量，它随着光线的传播而发生变化。${\theta }_0$是射线在起始点的发射角，由图3的几何可以看出，横截面积就是斜边

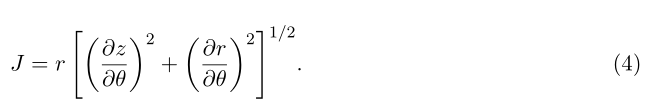
这个额外的$r$说明了一个假设，就是我们假设圆柱是一个对称形状的。所以图3只是显示了一个环绕$z$轴旋转的射线管的切面。
横截面积可以使用卡尺放在射线轨迹上来进行近似——即使用有限差分来近似，下面就是近似值：

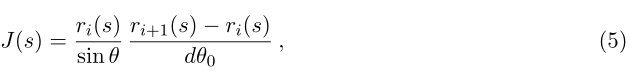
其中$r_i$和$r_{i+1}$是行程射线管的包围射线，而$\theta$是弧长$s$处的局部掠射角。
如同在光学之中，光线照射到海底或者表面就会行程反射。如果反射遵守反射角等于入射角的规则。如果一条射线从海底反射回来有6dB的损失，由此估计一下压力的损失。

声压通常使用传输损耗来进行表示，传输损耗是沿着射线路径振幅相对变化的对数度量。参考值是1m处的压力值。

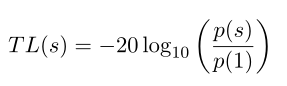
使用归一化方程式时，$p(1)=1/4\pi$。参考见式子（3）

4.线性声速剖面

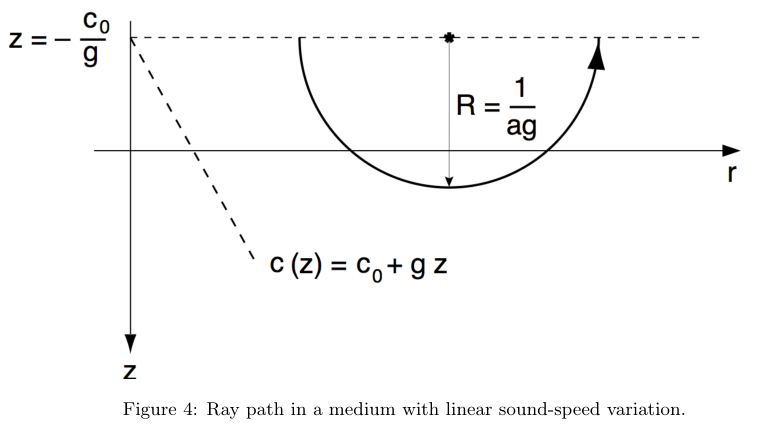
在深度和声速线性分布的海洋中

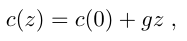
声速的路径是一个圆弧，圆圈是以声速消失的线为中心。

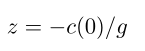
并且具有任意半径

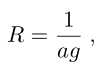
这具体取决于$a$的大小，如图4所示

$a$的值主要由射线的初始条件所决定。因此，对于以深度$z_0$和掠射角${\theta }_0$的射线来说，根据斯涅耳定律，最深点$z_{max}$转折点处的声速为：

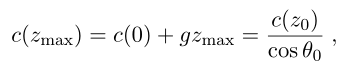
深度：

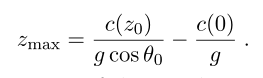
最后一项是圆弧中心的深度，因此第一项是半径：

因此可变参数$a$是斯涅耳定律中的一个常数

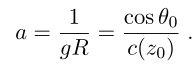
现在可以很容易的计算射线的路径和范围，所以弧长为：

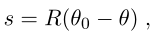
圆弧的简单投影：

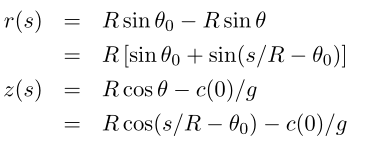
总结

因为本章实验的仿真过程需要涉及到MIT的服务器的使用，所以实验无法进行。所以主要内容是关于海洋声学知识内容的理解。

最后

以上就是俏皮小懒虫为你收集整理的MOOS-ivp 实验六 海洋声学环境MOOS-ivp 实验六 海洋声学环境前言一、海洋声学环境总结的全部内容，希望文章能够帮你解决MOOS-ivp 实验六 海洋声学环境MOOS-ivp 实验六 海洋声学环境前言一、海洋声学环境总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。