决策树概述

决策树相当于if-then的感觉，从树的根节点出发，进行判断。其中非叶子节点是特征的筛选。现在机器学习中用的比较多的算法xgboost以及gbdt都是以决策树作为基础，准确的说是回归树，采用cart树。简单的说分类树，比如判断第一次见面判断一个人是否有钱，打扮是否整洁？衣服/鞋子/裤子是否是牌子货？手机品牌？车钥匙？等等
当我们的因变量为类别的时候，就是分类决策树，可以采用id3或者id4.5或者cart算法进行。当因变量为连续值的时候，只能使用cart算法了。
给定训练集

$$D={(x_1,y_1),(x_2,y_2),(x_3,y_3)......}$$
其中 $x_i=(x_i^1,x_i^2,x_i^3......x_i^n)$为输入实例，有n个特征。现在需要解决的问题就是选取哪个特征进行怎样的划分使得划分的空间能够更好的总结数据的规则？不同的算法有不同的划分办法，这里将算法根据因变量进行了划分，因为两种方式的损失是不一样的，分类算法讲究的是纯度的提升，而回归的算法讲究的是均方误差的降低。

因变量为类别——分类树

分类树就是因变量是类别。上节已经讲到，做分类树目标是每一次划分使得节点纯度的一个提升。下面的三种算法采用了不同的策略。

ID3以及ID4.5算法

对于ID3算法而言，采用的是信息增益进行划分；ID4.5则采用的是信息增益比进行划分。介绍信息增益之前先介绍熵，熵表示随机变量的不确定性。假设一个离散随机变量X的概率分布为：

$$P(x=x_i)=p_i,i=1,2,3......$$
则随机变量的熵为：
$$H(x)=-sum_{i=1}^{n}p_ilogp_i$$
举个例子，假设有一堆球，只有红色，那么随机的从里面抽取到球为红色的概率为1，抽取生产的变量的熵为0，若有2种颜色，概率相等，那么其熵为： $-(0.5log0.5+0.5log0.5)=log2$。当随机变量是均匀分布的时候，熵达到最大，因为这个时候不确定性最大。
熵越大表明变量的不确定性越大，越小则表示越确定
对于分类决策树来说，我们需要找到一个特征，使其分化的节点的熵越来小。其实这个时候我们已经可以设计算法了，只要找到一个特征，使得分离后的熵越来越小，但是如果这个熵比分离前还大，那就没有必要了，所以发明了一个东西叫信息增益，就是分离前的熵和分离后的熵之差。信息增益越大越好。
介绍信息增益前先介绍条件熵，若随机变量(X,Y)的概率分布为：
$$P(X=x_i,Y=y_j)=p_{ij},i=1,2,3......n,j=1,2,3......m$$
条件熵H(Y|X)为：
$$H(Y|X)=sum_{i=1}^{n}p_iH(Y|X=x_i)$$
简单的理解就是，我们在已知X的情况下，对集合进行了分离，分离后的每个集合的熵的期望就是条件熵。

信息增益：若一个集合D的熵为H(D),在特征A给定条件下的D的条件熵为H(D|A),信息增益为：

$$g(D,A)=H(D)-H(D|A)$$
这里借助《机器学习》——周志华的书中的例子：

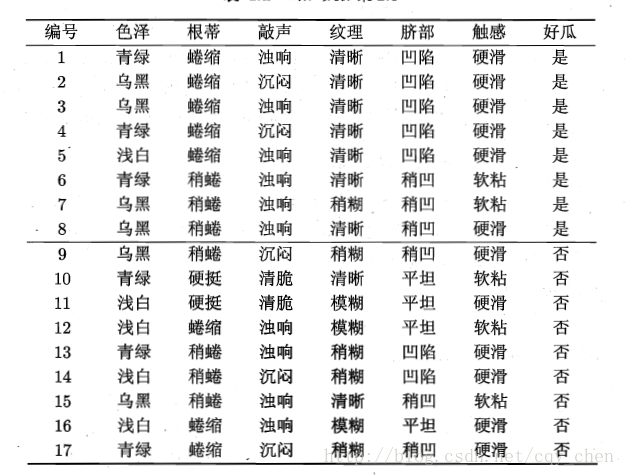
我们以色泽这个特征为例，首先计算整个集合的熵,整个集合有两个类别，正的8个，负的9个：

$$H(D)=-(frac{8}{17}logfrac{8}{17}+frac{9}{17}logfrac{9}{17})=0.998$$
色泽有3种可取值，（乌黑，浅白，青绿）。根据这三种取值将整个集合分成三块，每一块的熵为：
$$H(D|色泽=乌黑)=-(frac{4}{6}logfrac{4}{6}+frac{2}{6}logfrac{2}{6})=0.918$$
$$H(D|色泽=青绿)=-(frac{3}{6}logfrac{3}{6}+frac{3}{6}logfrac{3}{6})=1$$
$$H(D|色泽=浅白)=-(frac{1}{5}logfrac{1}{5}+frac{4}{5}logfrac{4}{5})=0.722$$
最后我们计算以特征色泽进行划分得到的信息增益：

$$begin{equation} begin{aligned} g(D|色泽)&=H(D)-(frac{6}{17}H(D|色泽=乌黑)+frac{6}{17}H(D|色泽=青绿)+frac{5}{17}H(D|色泽=浅白))\ &=0.998-(frac{6}{17}*0.918+frac{6}{17}*1+frac{5}{17}*0.722)\ &=0.109 end{aligned} end{equation}$$
说明通过色泽进行划分使得原始的集合的纯度得到了提升。同理我们也可以计算其他特征进行划分的信息增益。
ID3算法就是采用信息增益进行了划分。但是这里只是介绍了离散值的情况，如果对于连续值呢？
如果特征是连续的，我们将特征进行排序，然后找到一个切分点，将数据集分成2类，使得在该切分点下信息增益最大。
假设 $x=(x_1,x_2,x_2......x_n)$表示数据集的一个特征，该特征值为连续值，这个时候工有n-1个切分点可以将x分成两类，空集和全集舍去。在该切分点下，使得信息增益最大。
总的来说如果特征是离散的，直接划分计算信息增益即可，如果是离散的，就要扫描n-1个划分点，计算n-1次的信息增益，是比较麻烦的。

ID3算法的计算步骤如下：
1）计算数据集的熵H(D)
2）依次计算各个特征的条件熵，假设特征A,则为H(D|A)
3）计算各个特征的信息增益
4）挑选信息增益最大的特征为本次划分
5）递归执行划分
本人在博客中已经有代码实现，可以参考：
http://blog.csdn.net/cqy_chen/article/details/69803181
最后生成的决策树如下：

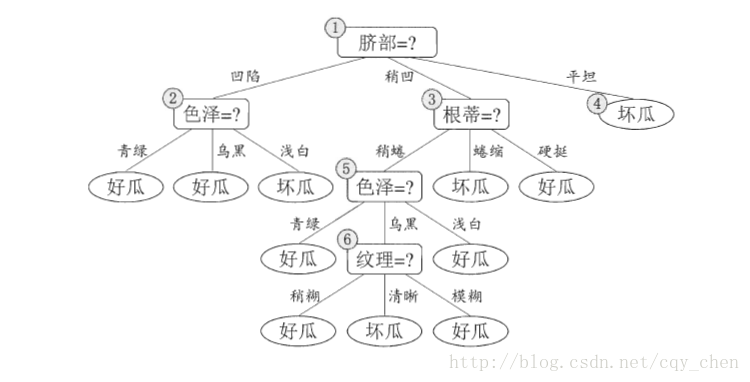
其实我们在公式中可以看到，ID3算法偏向于取属性多的特征，因为特征属性越多，我们进行切分之后的提纯效果越好，假设特征属性就一个，那不用想划分前和划分后没区别，信息增益0，木有意义的划分。
为了解决这个问题，提出了ID4.5算法，采用了信息增益率的方式。
信息增益率：设特征A对训练数据集的信息增益比为g(D,A),训练数据关于特征A的划分的熵定义为：

$$H_A=-sum_{i}^{k}frac{|D_i|}{|D|}log_{2}frac{|D_i|}{|D|}$$
注意这是以2为底，至于为啥用2，不用e，偶也不知道。应该是信息的单位不一样，赶脚e应该也可以。如果哪位大虾知道，请不吝赐教。
信息增益率就为：
$$g_r(D,A)=frac{g(D,A)}{H_A}$$
ID4.5即采用信息增益率为划分标准。

cart算法

cart树是一个二叉树，所以在选择特征的时候，只会将一个特征的值分成两类，比如上面的色泽特征属性值有：{浅白、青绿、乌黑}，cart树只会将其成两部分{（浅白）（青绿、乌黑）}、{（青绿），（浅白、乌黑）}、{（乌黑）（浅白、青绿）}，即使有n个属性值，也只会有n中分类，其中一个值一类，另外的值算做一类。
cart算法既可以做分类又可以做回归，在因变量为离散值的时候，采用基尼指数作为划分标准。假设一个离散随机变量X的概率分布为：

$$P(x=x_i)=p_i,i=1,2,3......n$$
则数据集的基尼指数为：
$$Gini(x)=sum_{i=1}^{n}p_i(1-p_i)=1-sum_{i=1}^{n}p_i^2$$
我们可以对比下熵：
$$H(x)=-sum_{i=1}^{n}p_ilogp_i$$
其实基尼指数约等于熵的一半。 $Gini(x)approx0.5*H(x)$, 且 $Gini(x)leq0.5*H(x)$
当对一个特征进行分类后，将原始数据集D分成了两个数据集记做 $D_1、D_2$.则在特征A的条件下，集合D的基尼指数是两个分开后的数据集的基尼指数的权重之和
$$Gini(D,A)=frac{|D_1|}{|D|}Gini(D_1)+frac{|D_1|}{|D|}Gini(D_2)$$
我们同样以上面的色泽为例，我们需要算出色泽在各个特征值下的基尼指数：
$$begin{equation} begin{aligned} Gini(D,色泽=青绿)&=frac{6}{17}*(frac{3}{6}*(1-frac{3}{6})+frac{3}{6}*(1-frac{3}{6}))+frac{9}{17}*(frac{5}{11}*(1-frac{5}{11})+frac{6}{11}*(1-frac{6}{11}))\ &=0.43898881866796313 end{aligned} end{equation}$$
同理我们可以计算其他的特征及其分割点。然后选择最优的特征及其分割点，Gini指数越小越好。这里就不做演示了。
对于连续值来说，和上面讲的一样，特征值有n个属性，则有n-1个划分点。找到最优特征及其划分点就好了。

因变量为连续值——回归树

cart算法

当因变量为连续值的时候，我们需要使得树所划分的空间的值和真实值的均方误差达到最小。
有训练数据集：$D={(x_1,y_1),(x_2,y_2)......(x_n,y_n)}$，其中y是连续值，而x可以是连续的也可以是离散的。设回归树已经将特征空间划分为M个单元$R_1,R_2......R_m$,且对应的值为$c_1,c_2......c_m$则回归树的模型为：

$$f(x)=sum_{m=1}^{m}c_mI(xin{R_m}),I为指示函数，表示改点是否属于该划分区域$$
这时候我们的损失函数为：
$$L=sum_{xin{R_m}} (y_i-f(x_i)^2$$
我们的目的就是使其最小化。其实上面的介绍，对于回归的问题，也是很好做的。现在剩下的问题就是如何进行特征的选取以及特征的划分了。
在使用cart做分类的时候，采用的是Gini指数，这里采用的是均方误差。
假设特征A为连续值，离散值也无所谓的。属性值从小到大进行排列为 $(x_1,x_2,x_3......x_n)$,共n-1个划分点。选取划分点为s。整个数据集划分为两块：
$$D_1={x|x<=s} ,D_2={x|x>s}$$
其中 $D_1对应的值c_1=avg(y_i|y_iin{D_1})$,我们以均值作为数据集的输出。同理D_2也是类似。
我们需要使得：
$$min[min_{c_1}sum_{x_iin{D_1}}(y_i-c_1)^2+min_{c_2}sum_{x_iin{D_2}}(y_i-c_2)^2]$$
找到一个特征的最优划分就好了。递归进行操作。就完成了回归树。
后面代码在我写GBDT的时候会进行展示，因为GBDT是依赖于回归树的。

最后

以上就是儒雅电源为你收集整理的机器学习之决策树决策树概述因变量为类别——分类树因变量为连续值——回归树的全部内容，希望文章能够帮你解决机器学习之决策树决策树概述因变量为类别——分类树因变量为连续值——回归树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。