目录
- 分类树与回归树
- 回归树
- 原理介绍
- 最小二乘回归树生成算法
- CART算法
- 原理介绍
- Python代码
- 节点类
- 回归树类
- 简单的例子
- Python库
分类树与回归树
分类树用于分类问题。分类决策树在选取划分点,用信息熵、信息增益、或者信息增益率、或者基尼系数为标准。
Classification tree analysis is when the predicted outcome is the class to which the data belongs.
回归决策树用于处理输出为连续型的数据。回归决策树在选取划分点,就希望划分的两个分支的误差越小越好。
Regression tree analysis is when the predicted outcome can be considered a real number (e.g. the price of a house, or a patient’s length of stay in a hospital)。
回归树
英文名字:Regression Tree
原理介绍
决策树最直观的理解其实就是,输入特征空间((R^n)),然后对特征空间做划分,每一个划分属于同一类或者对于一个输出的预测值。那么这个算法需要解决的问题是1. 如何决策边界(划分点)?2. 尽可能少的比较次数(决策树的形状)
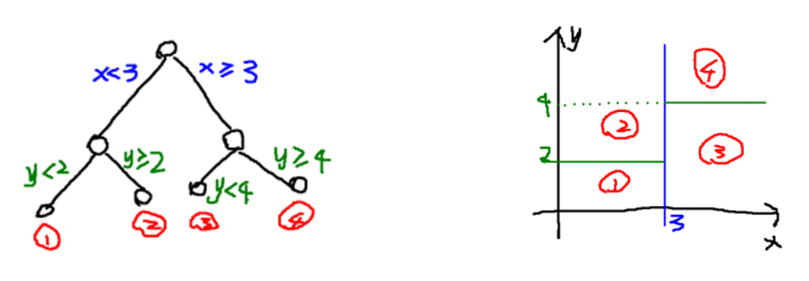
如上图,每一个非叶子对于某个特征的划分。
最小二乘回归树生成算法
Q1: 选择划分点?遍历所有的特征((n)),对于每一个特征对应(s_i)个取值,尝试完所有特征,以及特征所以有划分,选择使得损失函数最小的那组特征以及特征的划分取值。
Q2: 叶节点的输出?取每个区域所以结果的平均数作为输出
节点的损失函数的形式
[ min _{j, s}left[min _{c_{1}} Loss(y_i,c_1)+min _{c_{2}} Loss(y_i,c_2)right] ]
节点有两条分支,(c1)是左节点的平均值,(c2)是右节点的平均值,换句话说,分一次划分都是使得划分出的两个分支的误差和最小。最终得到函数是分段函数
CART算法
输入: 训练数据集
输出:回归树(f(x))
选择最优的特征(j)和分切点(s)
[ min _{j, s}left[min _{c_{1}} sum_{x_{i} in R_{1}(j, s)}left(y_{i}-c_{1}right)^{2}+min _{c_{2}} sum_{x_{i} in R_{2}(j, s)}left(y_{i}-c_{2}right)^{2}right] ]对于选定的((j,s))划分区域,并确定该区域的预测值
对两个区域递归1. 2. 直到满足停止条件
返回生成树
注:分切点选择:先排序,二分。
Python代码
节点类
属性:左右节点、loss、特征编号或者特征、分割点
class Node(object):
def __init__(self, score=None):
# 构造函数
self.score = score
self.left = None
self.right = None
self.feature = None
self.split = None回归树类
构造方法
class RegressionTree(object):
def __init__(self):
self.root = Node()
self.height = 0给定特征、划分点,返回计算MAPE
def _get_split_mse(self, X, y, idx, feature, split):
'''
X:训练样本输入
y:训练样本输出
idx:该分支对应的样本编号
feaure: 特征
split: 划分点
'''
split_x1=X[X[idex,feature]<split]
split_y1=y[X[idex,feature]<split]
split_x2=X[X[idex,feature]>=split]
split_y2=y[X[idex,feature]>=split]
split_avg = [np.mean(split_y1), np.mean(split_y2)]
split_mape = [np.sum((split_y1-split_avg[0])**2),np.sum((split_y2-split_avg[1])**2)]
return split_mse, split, split_avg计算给定特征的最佳分割点
遍历特征某一列的所有的不重复的点,找出MAPE最小的点作为最佳分割点。如果特征中没有不重复的元素则返回None。
def _choose_split_point(self, X, y, idx, feature):
feature_x = X[idx,feature]
uniques = np.unique(feature_x)
if len(uniques)==1:
return Noe
mape, split, split_avg = min(
(self._get_split_mse(X, y, idx, feature, split)
for split in unique[1:]), key=lambda x: x[0])
return mape, feature, split, split_avg选择特征
遍历全部特征,计算mape,然后确定特征和对应的切割点,注意如果某个特征的值是一样的,则返回None
def _choose_feature(self, X, y, idx):
m = len(X[0])
split_rets = [x for x in map(lambda x: self._choose_split_point(
X, y, idx, x), range(m)) if x is not None]
if split_rets == []:
return None
_, feature, split, split_avg = min(
split_rets, key=lambda x: x[0])
idx_split = [[], []]
while idx:
i = idx.pop()
xi = X[i][feature]
if xi < split:
idx_split[0].append(i)
else:
idx_split[1].append(i)
return feature, split, split_avg, idx_split对应叶子节点,打印相关的信息
def _expr2literal(self, expr):
feature, op, split = expr
op = ">=" if op == 1 else "<"
return "Feature%d %s %.4f" % (feature, op, split) 建立好二叉树以后,遍历操作
def _get_rules(self):
que = [[self.root, []]]
self.rules = []
while que:
nd, exprs = que.pop(0)
if not(nd.left or nd.right):
literals = list(map(self._expr2literal, exprs))
self.rules.append([literals, nd.score])
if nd.left:
rule_left = []
rule_left.append([nd.feature, -1, nd.split])
que.append([nd.left, rule_left])
if nd.right:
rule_right =[]
rule_right.append([nd.feature, 1, nd.split])
que.append([nd.right, rule_right])建立二叉树的过程,也就是训练的过程
- 控制深度
- 控制节叶子节点的最少样本数量
- 至少有一个特征是不重复的
def fit(self, X, y, max_depth=5, min_samples_split=2):
self.root = Node()
que = [[0, self.root, list(range(len(y)))]]
while que:
depth, nd, idx = que.pop(0)
if depth == max_depth:
break
if len(idx) < min_samples_split or set(map(lambda i: y[i,0], idx)) == 1:
continue
feature_rets = self._choose_feature(X, y, idx)
if feature_rets is None:
continue
nd.feature, nd.split, split_avg, idx_split = feature_rets
nd.left = Node(split_avg[0])
nd.right = Node(split_avg[1])
que.append([depth+1, nd.left, idx_split[0]])
que.append([depth+1, nd.right, idx_split[1]])
self.height = depth
self._get_rules()打印叶子节点
def print_rules(self):
for i, rule in enumerate(self.rules):
literals, score = rule
print("Rule %d: " % i, ' | '.join(
literals) + ' => split_hat %.4f' % score)
预测单样本
def _predict(self, row):
nd = self.root
while nd.left and nd.right:
if row[nd.feature] < nd.split:
nd = nd.left
else:
nd = nd.right
return nd.score
# 预测多条样本
def predict(self, X):
return [self._predict(Xi) for Xi in X]
def main():
print("Tesing the accuracy of RegressionTree...")
X_train=np.array([[1],[2],[3],[4],[5],[6],[7],[8],[9],[10]])
y_train=np.array([[5.56 ],[5.7],[5.91],[6.4
],[6.8],[7.05],[8.9],[8.7
],[9 ],[9.05]])
reg = RegressionTree()
print(reg)
reg.fit(X=X_train, y=y_train, max_depth=3)
reg.print_rules()
main()简单的例子
训练数据
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 5.56 | 5.7 | 5.91 | 6.4 | 6.8 | 7.05 | 8.9 | 8.7 | 9 | 9.05 |
根据上表,只有一个特征(x).
选择最优的特征(j)和分切点(s)
分切点(s) 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 (c_1) 5.56 5.63 5.72 5.89 6.07 6.24 6.62 6.88 7.11 (c_2) 7.5 7.73 7.99 8.25 8.54 8.91 8.92 9.03 9.05 loss 15.72 12.07 8.36 5.78 3.91 1.93 8.01 11.73 15.74 当分切点取(s=6.5),损失最小(l(s=6.5)=1.93),此时划分出两个分支,分别是(R_1={1,2,3,4,5,6}),(c_1=6.42),(R_2={7,8,9,10}),(c_2=8.91)
a) 对R1继续划分
x 1 2 3 4 5 6 y 5.56 5.7 5.91 6.4 6.8 7.05 分切点(s) 1.5 2.5 3.5 4.5 5.5 (c_1) 5.56 5.63 5.72 5.89 6.07 (c_2) 6.37 6.54 6.75 6.93 7.05 loss 1.3087 0.754 0.2771 0.4368 1.0644 当分切点取(s=3.5),损失函数(l(s=3.6)=0.2771)(假设此时满足停止条件),此时得到两个分支,分别是(R_1={1,2,3}),(c_1=5.72),(R_2={4,,5,6}),(c_2=6.75)
b) 对R2继续划分
x 7 8 9 10 y 8.9 8.7 9 9.05 分切点(s) 7.5 8.5 9.5 (c_1) 8.9 8.8 8.87 (c_2) 8.92 9.03 9.05 loss 0.0717 0.0213 0.0467 当分切点取(s=8.5),损失函数(l(s=8,5)=0.0213)(假设此时满足停止条件),此时得到两个分支,分别是(R_1={7,8}),(c_1=8.8),(R_2={9,10}),(c_2=9.03)
函数表达式
[ begin{equation} f(x)=left{ begin{aligned} 5.72 & & x<3.5\ 6.7 5& &3.5<=x<6.5\ 8.8& &6.5<=x<8.5\ 9.03& &8.5<=x<10\ end{aligned} right. end{equation} ]
Python库
class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort=False)# -*- coding: utf-8 -*-
"""
Created on Wed Mar 13 19:59:53 2019
@author: 23230
"""
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
X=np.array([[1],[2],[3],[4],[5],[6],[7],[8],[9],[10]])
y=np.array([[5.56 ],[5.7],[5.91],[6.4],[6.8],[7.05],[8.9],[8.7],[9 ],[9.05]])
# Fit regression model
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=3)
regr_3 = DecisionTreeRegressor(max_depth=4)
regr_1.fit(X, y)
regr_2.fit(X, y)
regr_3.fit(X, y)
X_test = np.copy(X)
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
y_3 = regr_3.predict(X_test)
# Plot the results
plt.figure()
plt.scatter(X, y, s=20, edgecolor="black",c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue",label="max_depth=2", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=4", linewidth=2)
plt.plot(X_test, y_3, color="r", label="max_depth=8", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()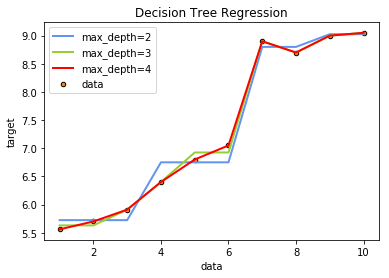
转载于:https://www.cnblogs.com/xiemaycherry/p/10540902.html
最后
以上就是自觉荷花最近收集整理的关于回归树分类树与回归树回归树Python代码简单的例子Python库的全部内容,更多相关回归树分类树与回归树回归树Python代码简单内容请搜索靠谱客的其他文章。








发表评论 取消回复