资料:https://blog.csdn.net/m0_37786726/article/details/79699972
资料:https://zhuanlan.zhihu.com/p/30059442
资料:https://www.cnblogs.com/bourneli/archive/2013/03/15/2961568.html
视频:https://www.bilibili.com/video/BV1Ps411V7px?from=search&seid=15068603710637202699&spm_id_from=333.337.0.0
决策树(Decision Tree)是一种简单但是广泛使用的分类器。主要用于处理分类问题(也能做回归)。
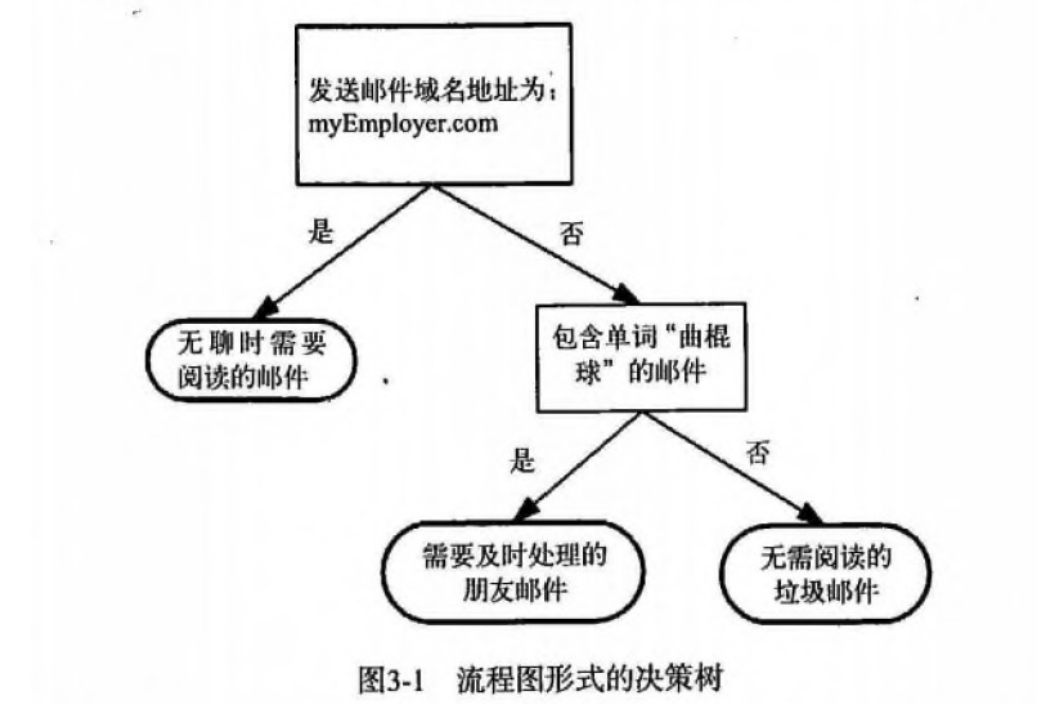
决策树构建的基本步骤
- 开始,所有记录看作一个节点
- 遍历每个变量的每一种分割方式,找到最好的分割点
- 分割成两个节点N1和N2
- 对N1和N2分别继续执行2-3步,直到每个节点足够“纯”为止
决策树变量有两种:
(1)数字型
(2)名称型

准备数据:只适用于标称型数据,因此数值型数据必须离散化
分析数据:构造树完成后,检查图形是否符合预期
训练算法:构造树的数据结构
测试算法:使用经验树计算错误率
优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
缺点:可能会产生过度匹配问题
信息熵:一种信息的度量方式,表示信息的混乱程度,信息越有序,信息熵越低
信息增益:划分数据集前后信息发生的变化称为**信息增益**
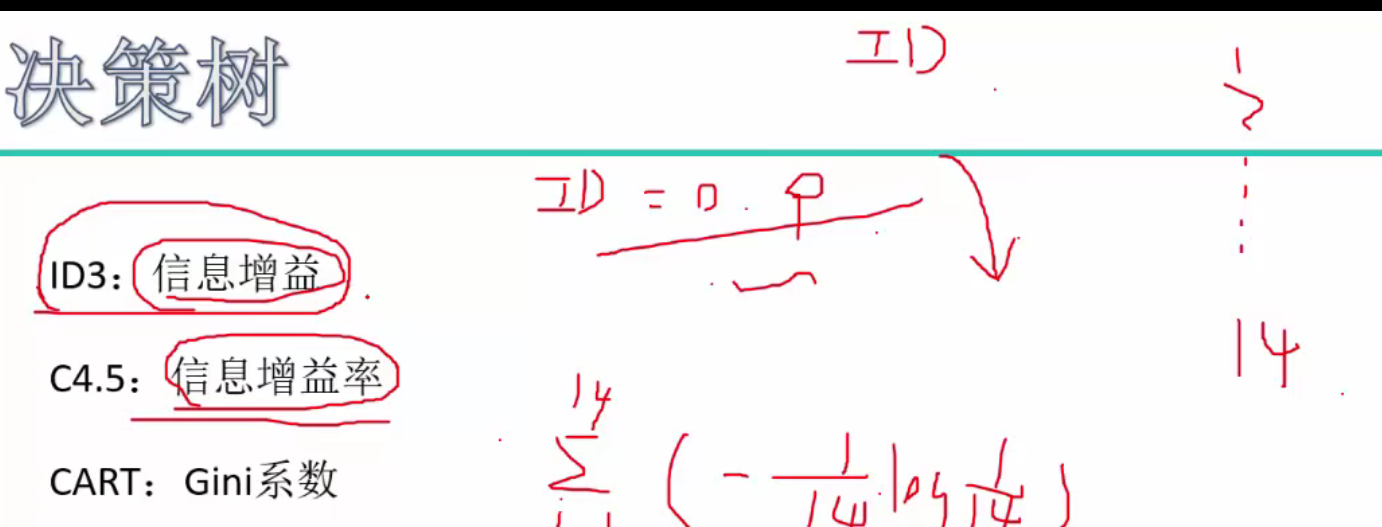
选择切割方式(量化纯度)的三个公式

熵

由增熵(Entropy)原理来决定那个做父节点,那个节点需要分裂。对于一组数据,熵越小说明分类结果越好。
Entropy=- sum [p(x_i) * log2(P(x_i) ]
其中p(x_i) 为x_i出现的概率。假如是2分类问题,当A类和B类各占50%的时候,
Entropy = - (0.5log_2( 0.5)+0.5log_2( 0.5))= 1
当只有A类,或只有B类的时候,
Entropy= - (1*log_2( 1)+0)=0
所以当Entropy最大为1的时候,是分类效果最差的状态,当它最小为0的时候,是完全分类的状态。因为熵等于零是理想状态,一般实际情况下,熵介于0和1之间。

计算给定数据集的香农熵的函数
...
for key in labelCounts:
# 使用所有类标签的发生频率计算类别出现的概率。
prob = float(labelCounts[key])/numEntries
# 计算香农熵,以 2 为底求对数
shannonEnt -= prob * log(prob, 2)
公式分析


信息增益/纯度差
决策树是根据“纯度”来构建的。纯度差也叫信息增益。
计算公式
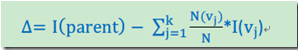
I代表不纯度(也就是上面三个公式的任意一种),K代表分割的节点数,一般K = 2。vj表示子节点中的记录数目。
信息熵的增益是指:所有属性值的信息熵和某一个属性值的信息熵的差值,增益值越大,说明其具有更高的决策性,可做为优先节点

最后选择分类错最少即熵最小的那个条件。而当分裂父节点时道理也一样,分裂有很多选择,针对每一个选择,与分裂前的分类错误率比较,留下那个提高最大的选择,即熵减最大的选择。
引入信息增益率
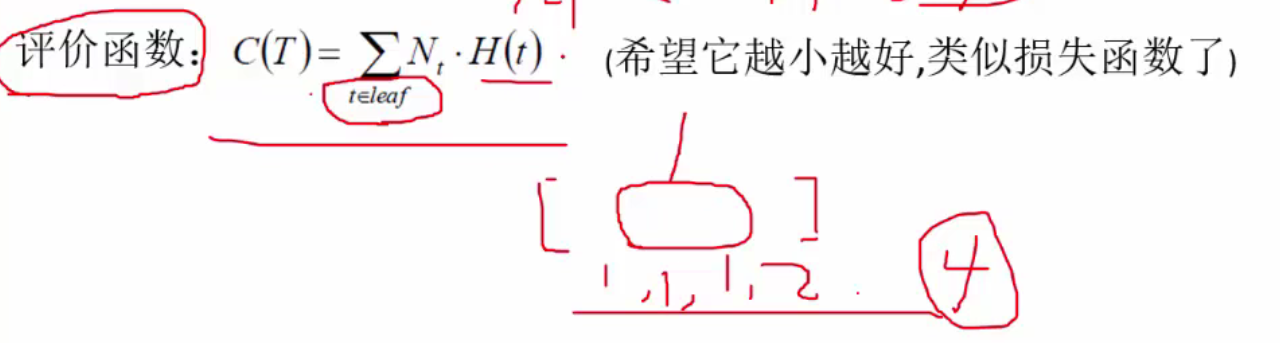
希望评价函数越小越好
连续值离散化–》分区间

停止分裂的条件
(1)最小节点数
当节点的数据量小于一个指定的数量时,不继续分裂。两个原因:一是数据量较少时,再做分裂容易强化噪声数据的作用;二是降低树生长的复杂性。提前结束分裂一定程度上有利于降低过拟合的影响。
”一种最直观的方式是当每个子节点只有一种类型的记录时停止,但是这样往往会使得树的节点过多,导致过拟合问题(Overfitting)。另一种可行的方法是当前节点中的记录数低于一个最小的阀值,那么就停止分割,将max(P(i))对应的分类作为当前叶节点的分类。“
(2)熵或者基尼值小于阀值。
由上述可知,熵和基尼值的大小表示数据的复杂程度,当熵或者基尼值过小时,表示数据的纯度比较大,如果熵或者基尼值小于一定程度时,节点停止分裂。
(3)决策树的深度达到指定的条件
节点的深度可以理解为节点与决策树跟节点的距离,如根节点的子节点的深度为1,因为这些节点与跟节点的距离为1,子节点的深度要比父节点的深度大1。决策树的深度是所有叶子节点的最大深度,当深度到达指定的上限大小时,停止分裂。
(4)所有特征已经使用完毕,不能继续进行分裂。
被动式停止分裂的条件,当已经没有可分的属性时,直接将当前节点设置为叶子节点。
过渡拟合
优化方案1:修剪枝叶
优化方案2:K-Fold Cross Validation
优化方案3:Random Forest
预剪枝与后剪枝


随机森林
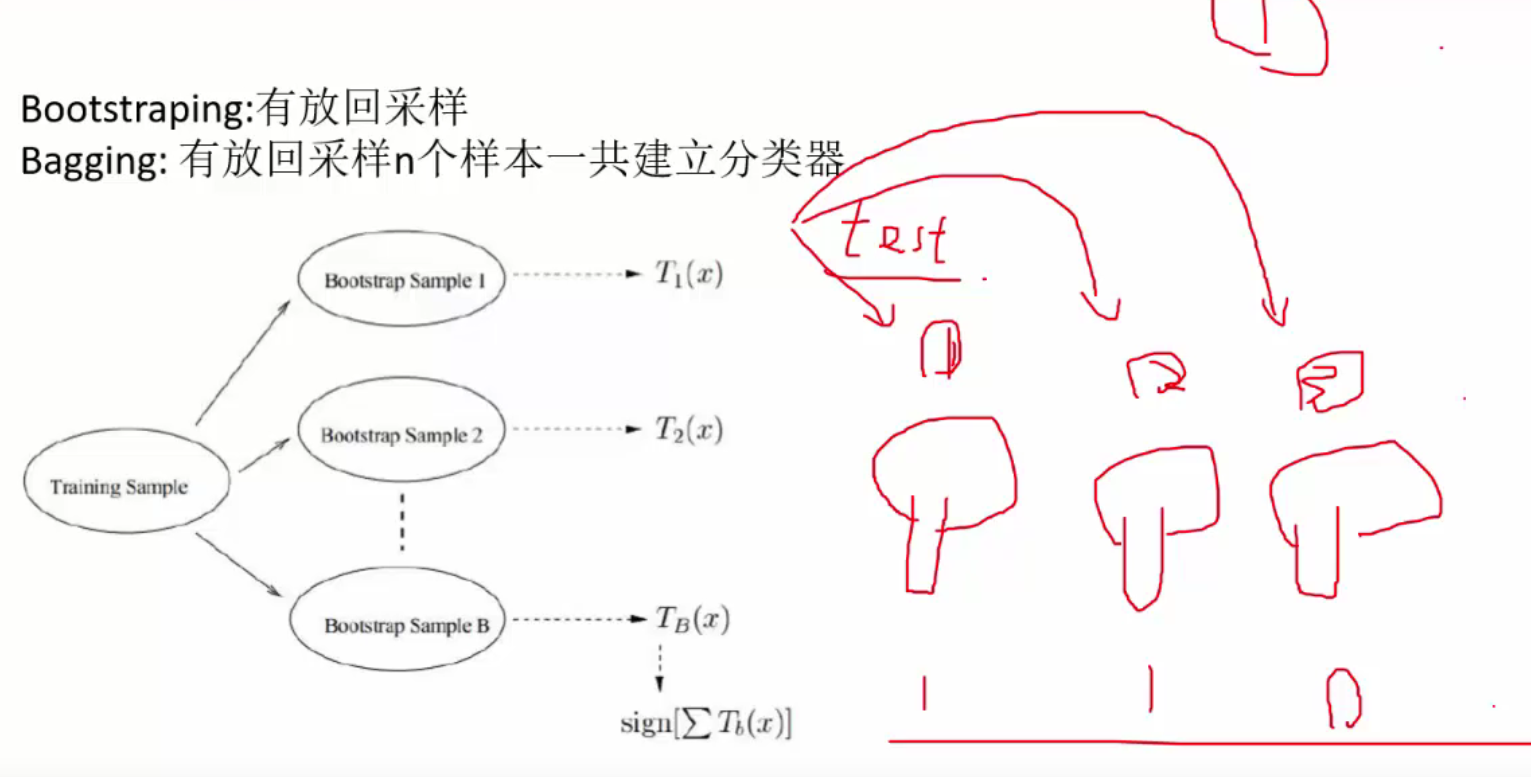

第一重随机性,样本选择的随机性
随机体现在每次构建决策树时不一定非要考虑所有样本,只随机选取一定量的样本构建树(有放回)
第二重随机性,特征选择的随机性
不一定要每次都选取所有的特征,可以选取部分
最后
以上就是优秀芹菜最近收集整理的关于决策树算法学习的全部内容,更多相关决策树算法学习内容请搜索靠谱客的其他文章。








发表评论 取消回复