decision tree Learning 决策树学习笔记

decision tree Learning 决策树学习笔记

一、概念和基本流程

   决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。决策树是一种监管学习方法，虽然简单，但是比较高效。目前比较常用和成功的算法有ID3和C4.5，本文也在后面将介绍。

决策树的决策过程如下图所示：

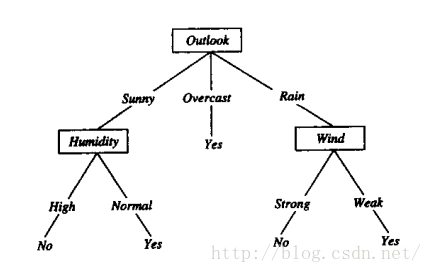
  结构呈树形结构，一般的，一颗决策树包含有一个根节点，若干个内部节点和若干个叶子节点。叶子节点对应的是决策的结果，即类别（如图中的yes和no两个类别）；其他的节点对应的是一个属性上的测试（如根节点是outlook属性，该属性分别有sunny、overcast、rain三个属性值）。

  决策树的学习递归算法create()如下所示：

输入：训练数据集D，特征集A

输出：决策树T

create()算法：

检验D中的所有实例是否都是属于同一个类，若是则返回该类标签；（出口1）

      否则：若特征集A为空集（用完所有可以分类的特征），则将D中实例数最大的类作为该节点的类标记返回；（出口2）

            否则：寻找划分数据集D的最好特征

                     划分数据集

                     创建分支节点

                     for 每个划分的子集

                               递归调用create()并增加返回结果到分支节点中

            返回分支节点

说明：

出口1是所以实例都属于同一个类，直接以该类作为叶子节点的类标签即可；

出口2是划分的特征用完了还没有将所有实例划分到同一个类别时，统计各个实例所属的类的实例数，取最多实例所对应的类作为该叶子节点的类标签；

算法的核心就在于寻找划分数据集D的最好特征这一个步骤，如何选取最好的特征，下面将详细介绍！

二、基本的决策树学习算法

1、ID3

ID3是一种以信息增益（information gain）作为最好特征选取原则的算法。

首先看一下什么是信息熵（information entropy），信息熵是一种度量样本集合纯度的指标，假设当前样本集合D中第k类样本所占的比例为pk(k = 1,2,3,...,|y|)，则D的信息熵定义为：

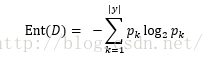
假定离散属性a有V个可能的取值{a1,a2,...,aV},如果使用属性a对样本集D进行分类的话，会产生V个分支节点，其中，第v个分支节点包含了D中所有在属性a上取值为av的样本子集，即Dv，该子集所占样本集的比例为|Dv|/|D|。所以，用属性a对样本集D划分所获得的信息增益（information gain）定义为：

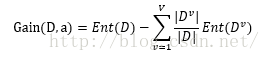
因此，我们可以算出所有属性的信息增益，从中选择当前的信息增益最大的属性作为划分数据集（样本集）D的最好特征。

缺点：ID3算法产生的决策树容易出现过拟合的问题，解决方法是剪枝！

2、C4.5

C4.5是一种以增益率（gain radio）作为最好特征选取原则的算法。可以克服以信息增益作为最优特征选取时，偏向于选择取值多的特征的问题。

增益率定义为：

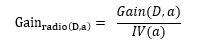
其中，IV(a)定义为：

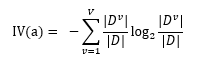
IV(a)是属性a的固有率，一般情况下，属性a的取值越多，IV(a)的值会越大，因此，增益率选择最优特征时，会和信息增益相反，偏向于选择取值少的特征。

但是，C4.5算法不是简单的选择取值最大的增益率作为特征选取的判断标准，而是采取了一个启发式规则：先找出信息增益高于平均水平的属性，再从中挑选增益率最高的属性作为最优属性。采取了信息增益和增益率两者的折中，优中选优！

本节重点介绍了决策树算法原理，以及ID3和C4.5两种特征选取算法。下节将给出一个Python版本的ID3算法的决策树小程序。

最后

以上就是独特小笼包为你收集整理的decision tree Learning 决策树学习笔记的全部内容，希望文章能够帮你解决decision tree Learning 决策树学习笔记所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。