代码：Generative Adversarial Networks (GANs)_iwill323的博客-CSDN博客

目录

概念

密度估计

 什么是生成模型

生成模型分类

 PixelRNN和PixelCNN

 PixelRNN

PixelCNN

 Variational Autoencoders (VAE)

 自编码器

VAE思想

如何训练VAE

生成数据

 总结

生成对抗网络GAN

GAN思路

目标函数

训练流程

GAN的探索

 总结

概念

密度估计

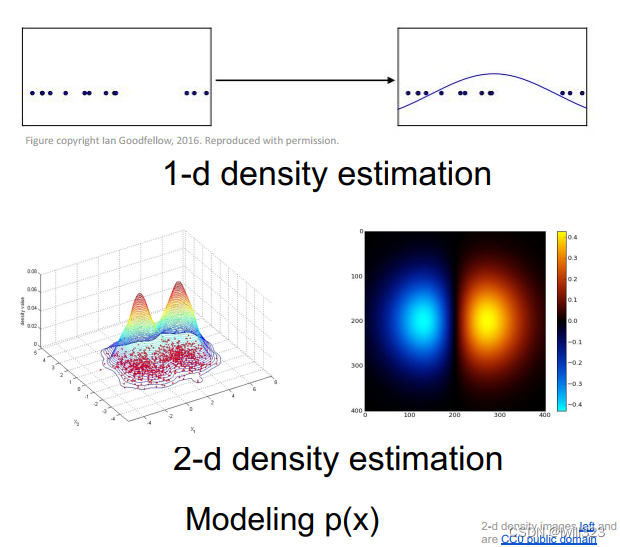
估计数据的内在分布情况，如下面两张图分别是一维和二维情况。

 什么是生成模型

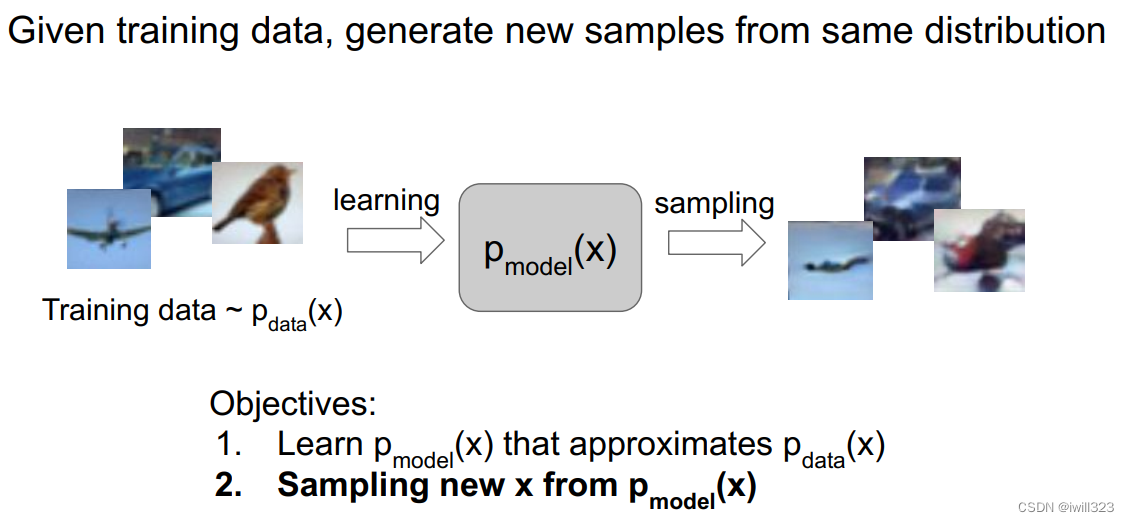
给定训练数据，训练一个模型，从相同的数据分布中生成新的样本。即下图所示，假设训练集满足分布 pdata(x)，训练一个模型pmodel(x)，它学习到的分布近似于pdata(x) ，然后用pmodel(x) 生成新样本

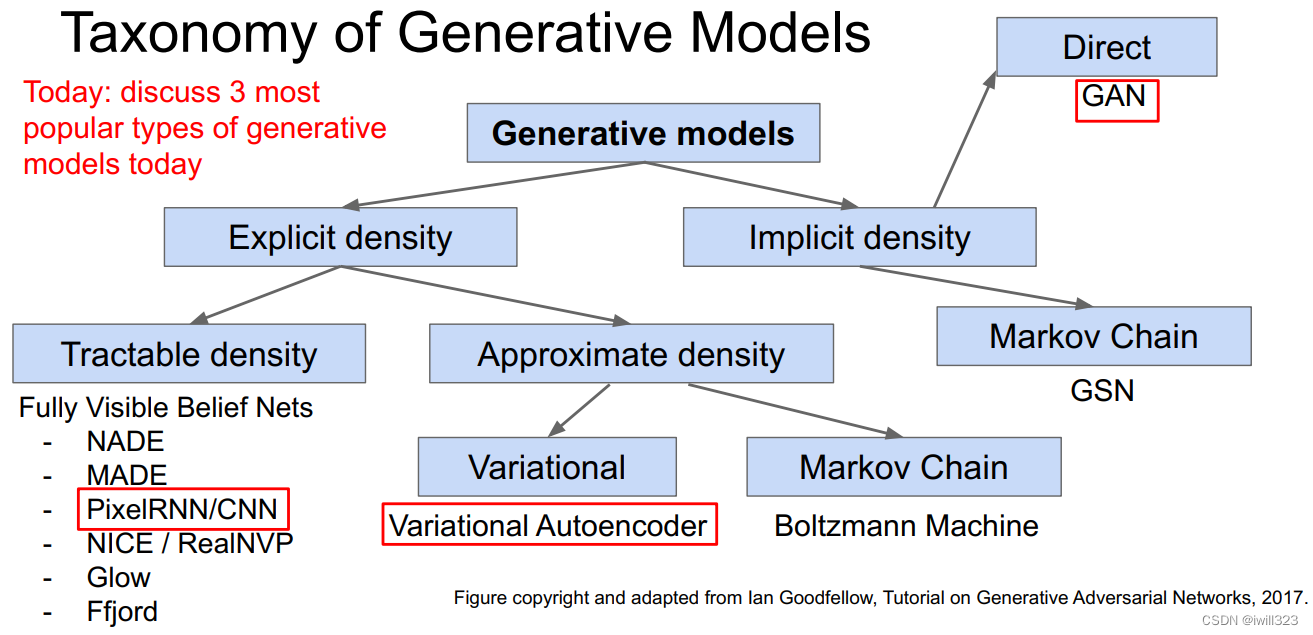
生成模型可以解决密度估计问题，有两种方式：

显式密度模型会显式地给出一个和输入数据的分布pmodel(x)

隐式密度模型训练一个模型，从输入数据中采样，并直接输出样本，而不用显式地给出分布的表达式。

生成模型分类

 PixelRNN和PixelCNN

PixelRNN和PixelCNN要做的是对图像像素概率分布进行建模。模型分解为像素值条件概率的乘积，其中每一项为给定前i-1个像素点后第i个像素点的条件概率分布，通过最大化该似然函数（认为输入的图片必然出现的概率应该是最大）来训练模型。显然，首先需要对像素进行排序

 PixelRNN

可以使用LSTM。从左上角开始一个个地生成像素。一个明显的缺点是按照顺序逐元素地计算并训练网络是十分慢的，同时在测试阶段，也是按照逐元素地生成像素，所以也会很慢

PixelCNN

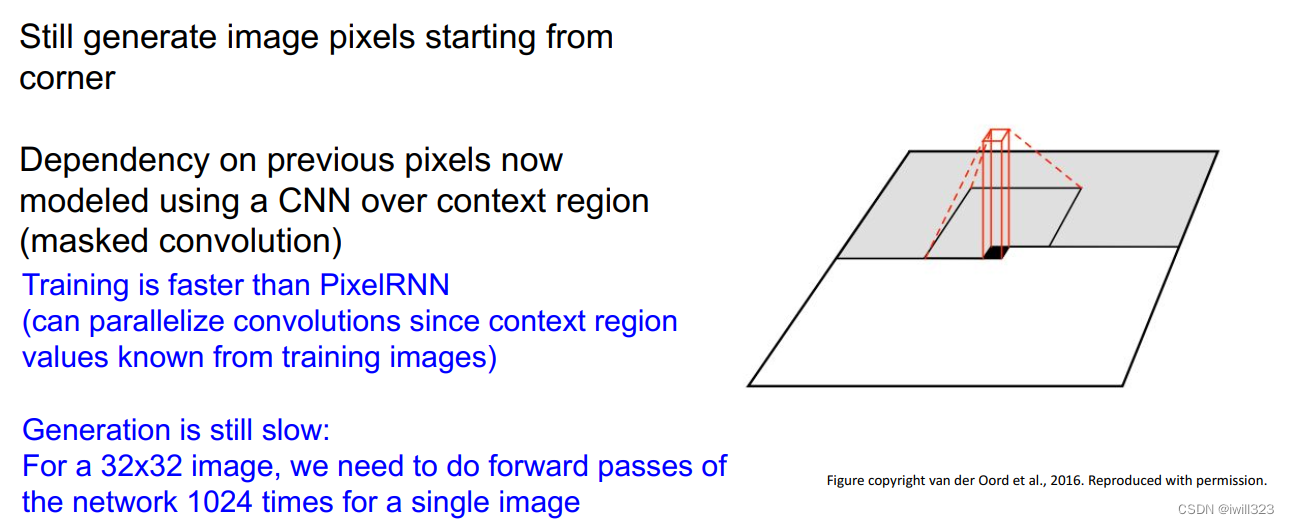
使用CNN来建模像素的依赖关系。如下图，灰色区域表示此时已经处理过的像素，当前正在处理黑色位置的像素。取待生成像素点周围的像素（下图黑色框），把它们传递给CNN用来生成下一个像素值，在每一个像素点上输出结果是像素的Softmax损失值，从而最大化输入图像的似然估计。训练的时候输入图片每个像素点的值都是ground truth，。确定了第一个像素，所有后面像素就基于它生成。

相比于pixelRNN，pixelCNN在训练时可以并行的求出公式中的每一项（因为上下文区域值从训练图像中已知），然后进行参数更新。然而，测试的时候仍然要逐一生成像素点，慢。

 生成的图像：分别用CIFAR-10和ImageNet作为训练集生成

 比较

 Variational Autoencoders (VAE)

VAE方法中定义了附加的隐变量z，通过隐变量z对密度函数进行建模，对所有可能的z值取期望。该函数不易处理，优化的时候实际上是优化似然函数的下界（？）

 自编码器

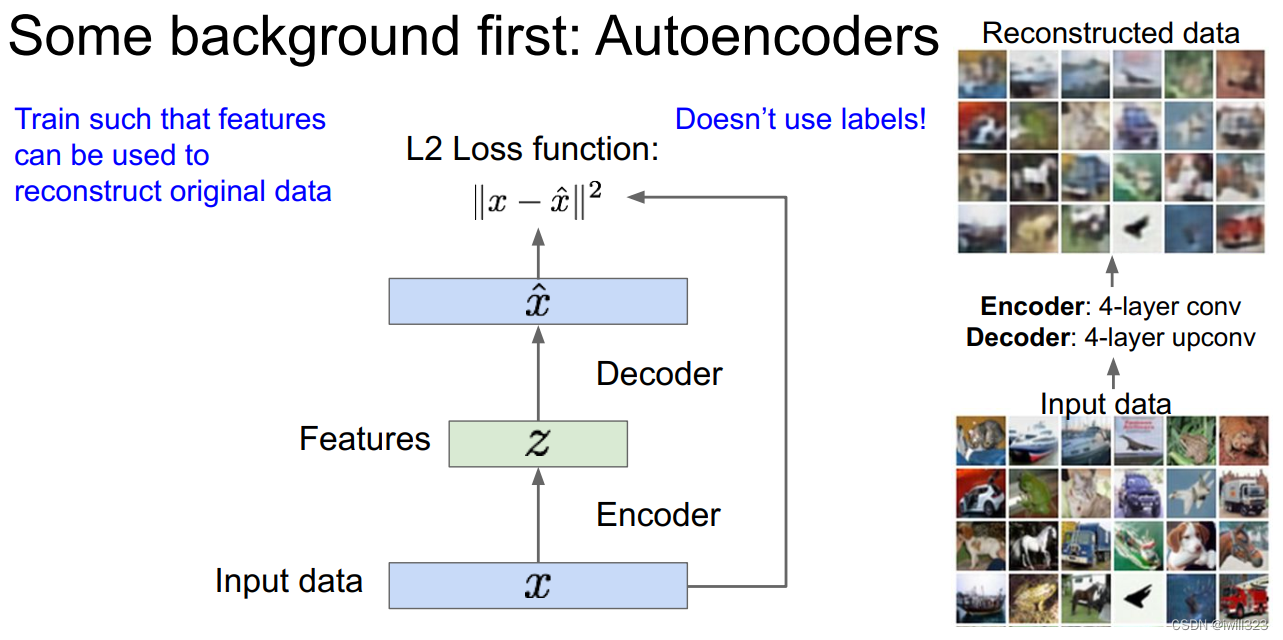
自编码器是为了从没有标注的数据中无监督地学习出样本的特征表示。

自编码器由编码器和解码器组成，编码、解码是对输入x的重构。

编码器将样本 x 映射到特征 z ，z的维度比x更低，因为z保留的是训练数据x中最重要的特征。

解码器使用特征 z 重构样本，输出跟 x 有相同维度的结果。解码器所用的网络一般和编码器一样。使用L2损失函数（输入的样本 x 与重构样本x^之间的 L2 损失），也就是尽量让重构后图像的像素值和输入图像一样 。

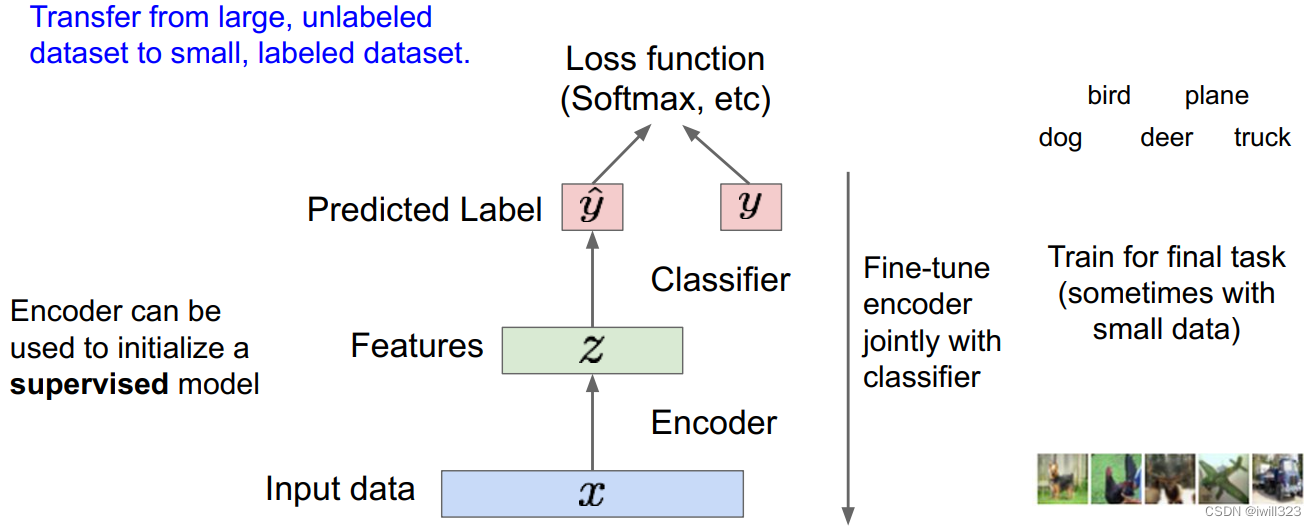
训练完之后丢掉解码器，使用训练好的编码器提取出输入的特征映射，然后使用这些特征初始化并训练一个监督模型（比如分类器）。

自编码器具有重构数据、学习数据特征、初始化一个监督模型的能力。使用无标签数据训练自编码器提取特征，作为监督学习的输入是非常有效的（有些场景下监督学习可能只有很少的带标签的训练数据，少量的数据很难训练模型，可能会出现过拟合等其他一些问题）。

VAE思想

神经网络只学会了对输入图片提取特征，并将这些特征恢复回图片，即只学会了对特定编码的解码。在码空间z里取其他值，神经网络连学都没学过，不可能正确地进行解码。所以就需要变分自编码器VAE。

VAE不是直接输出隐变量 z 而是输出图像的概率分布（假定为高斯分布）。求得z的概率分布，经过解码网络后映射得到x的近似真实分布，再在此分布上采样来生成样本。

如何训练VAE

如何从中学习出解码网络的参数，使得在标准高斯分布上采样得到的z，经过解码后得到的x的分布，刚好近似于x的真实分布？

方案是最大化样本x的似然P(x)。

在已经给定隐变量z的情况下，写出x的分布p并对所有可能的z值取期望，因为z值是连续的所以表达式是一个积分，便得到上面p(x)公示。神经网络可以模拟任意函数，所以可以通过神经网络对p(x|z)建模。问题是对于每一个z值计算p(x|z)很困难，所以积分无法计算

• 过程推导

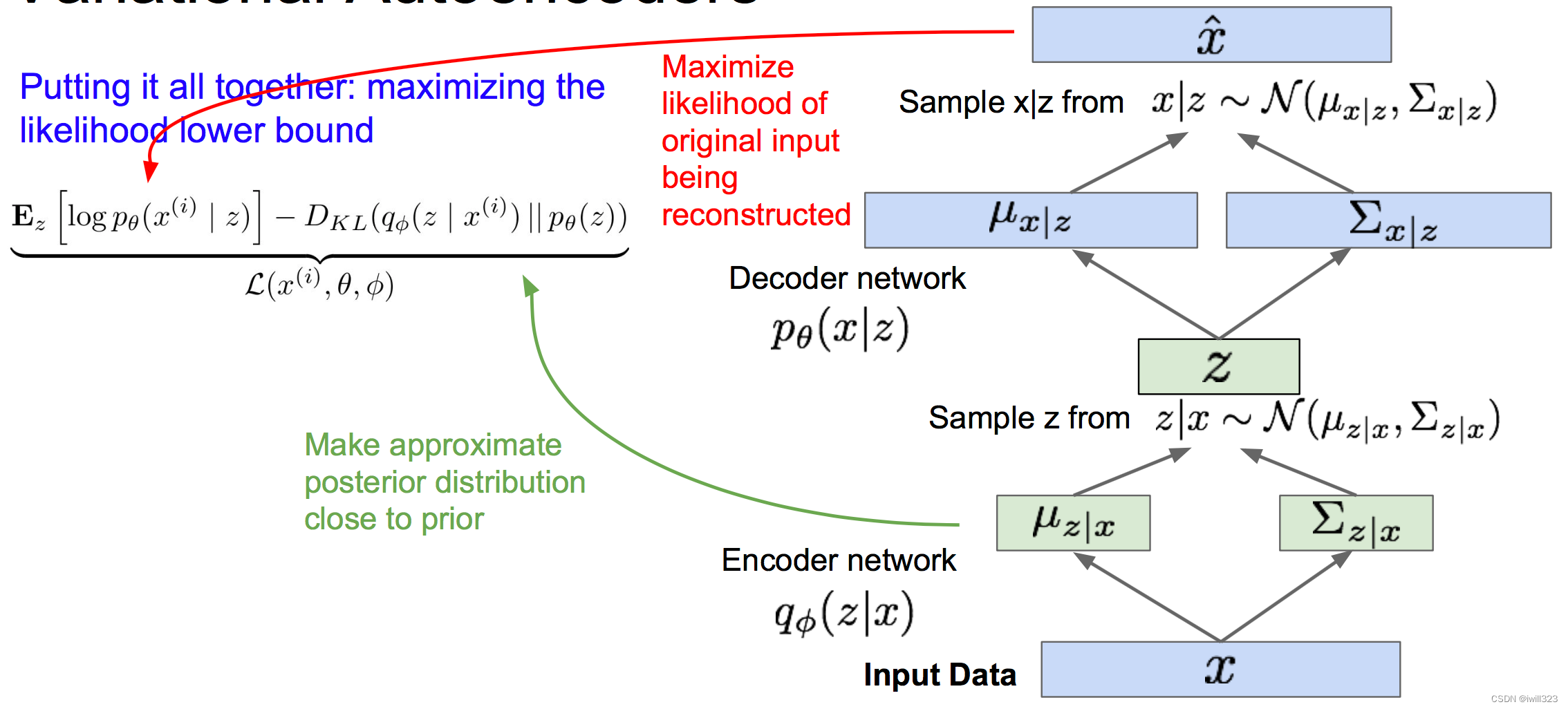
不直接求p(x)，而是求logp(x)。第一步logp(x)对z取期望，是因为p(x)不依赖于z（因为p(x)一旦求出来之后就和z无关了），这么做是为了后面方便地将log项转变为KL项（第5行）。

 注意到这个式子的第三项中含有p(z|x)，而

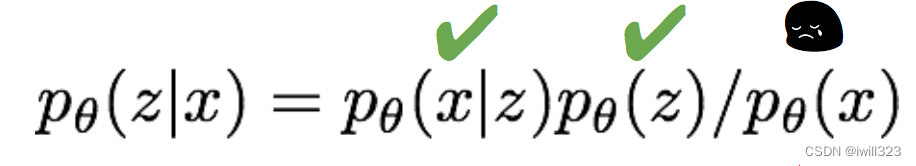
很遗憾p(x)本身就是我们要求的，所以p(z|x)没法求出来。幸运的是，由于第三项是一个KL散度，其恒大于等于0，因此前两项的和是似然的一个下界，而且这两项都是可微分的。因此我们退而求其次，来最大化似然的下界，间接达到最大化似然的目的。换句话说，这两项之和就是我们的损失函数。其中，第一项p(x|z)由解码器得到，q(z|x)由编码网络得到。采用该下界的合理性是，它相当于使用一个编码器 qɸ(z|x)来近似pθ(z|x)。p代表解码网络，q代表编码网络。

• 关于KL散度

KL散度详解_码猿小菜鸡的博客-CSDN博客_kl散度：KL散度（Kullback-Leibler Divergence）一般用于度量两个概率分布函数之间的“距离”。KL散度的典型应用场景如下：假设某优化问题中P(X) 是真实分布（true distribution），Q(X)是一个用于拟合P(X) 的近似分布（approximate distribution），可以尝试通过修改 Q(X) 使得二者间的KL[P(X) || Q(X)]尽可能小,来实现用 Q(X) 拟合P(X)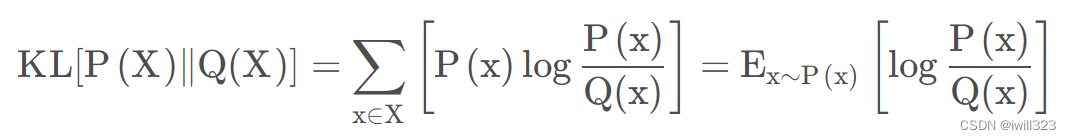

• 训练框架

训练的目的是学习出编码器的映射函数和解码器的映射函数，训练过程实际上是在进行变分推断，即寻找出某一个函数来优化目标，因此取名为变分编码器VAE(Variational Auto-encoder).

编码网络求出给定z下的x的均值μ、（对数）协方差∑，就得到了q(z|x)；p(z)的分布是N(0,I)。于是DKL项的解析式就得到了

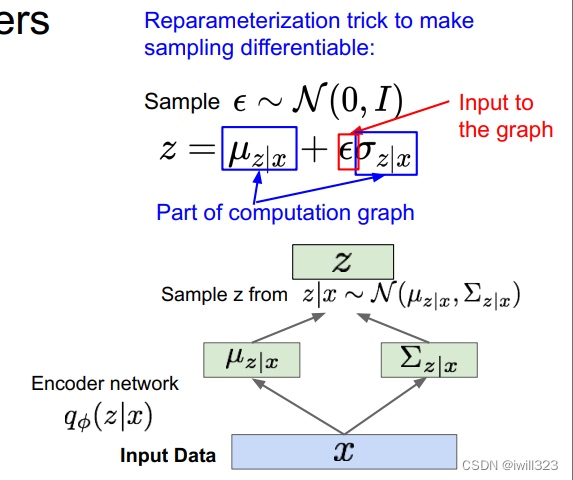
 解码网络求出给定x下的z的均值μ、（对数）协方差∑，就得到了p(x|z)。为了得到给定x下的z和给定z下的x，我们会从这些分布（p和q）中采样，现在我们的编码器和解码器网络所给出的分别是z和x的条件概率分布，并从这些分布中采样从而获得值。

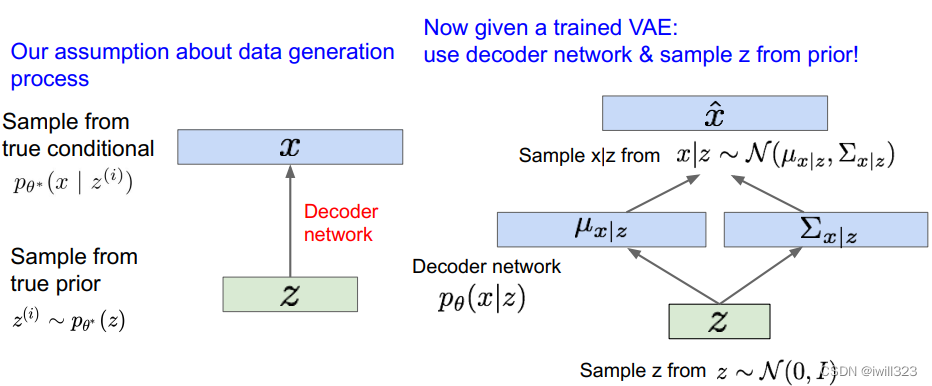
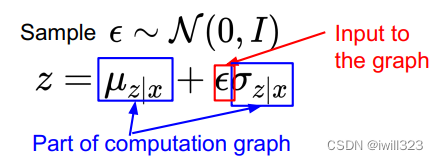
需要注意的是，“采样”这一行为无法包含在计算图内，计算完loss之后，梯度无法通过“采样”这个算子反向传播到编码器网络，因此使用一种叫做再参数化reparameterization的方法，将z采样的算子分解，这样梯度不需要经过采样算子就能回流到编码器网络中（图中的loss函数可能有点问题）

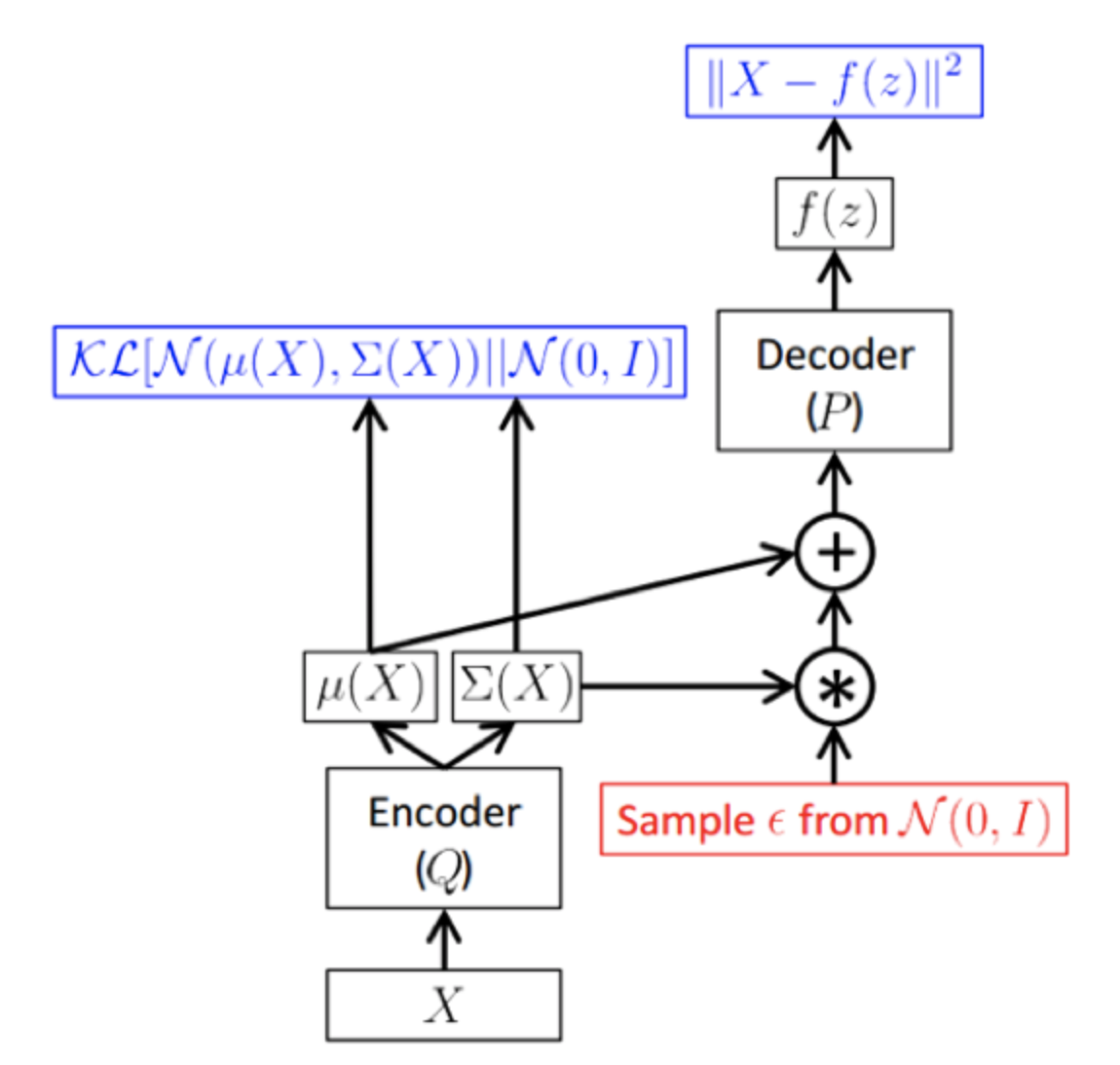
让小批量的数据传递经过编码器网络得到q(z|x)，通过q(z|x)来计算KL项，然后根据给定x的z分布对z进行采样，由此获得了隐变量的样本，这些样本可以根据x推断获得；然后把z传递给第二个解码器网络，通过解码器网络获得x在给定z的条件下的均值和协方差，最终可以在给定z的条件下从这个分布中采样得到x。
训练时损失项是给定z条件下对训练像素值取对数，损失函数要做的是最大化被重构的原始输入数据的似然。对于每一个小批量的输入我们都计算这一个前向传播过程，取得所有我们需要的项，他们都是可微分的，接下来把他们全部反向传播回去并获得梯度，不断更新我们的参数，包括生成器和解码器网络的参数Θ和Φ从而最大化训练数据的似然。

生成数据

训练好变分自编码器，当生成数据时只需要用解码器网络。先从设定好的先验分布中采样，接下来对数据x采样。
    在本例中通过在MNIST数据集上训练VAE，我们可以生成这些手写数字样本，我们用z表示隐变量，因为是从先验分布的不同部分采样，所以我们可以通过改变z来获得不同的可解释的意义。这里可以看到一个关于二维z的数据流形。让z在某个区间内变化，比如该分布的百分比区间，接下来让z1和z2逐渐变化，从这幅图中可以看到z1和z2的组合所生成的图像，它会在所有这些不同的数字之间光滑地过渡变化。

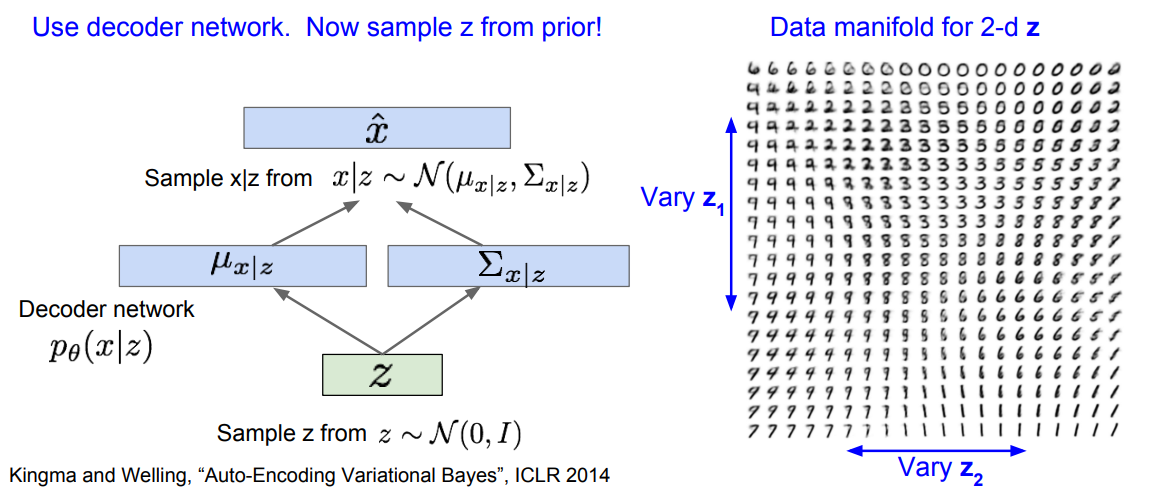
我们对z的先验假设是对角的，这样做是为了促使它成为独立的隐变量，这样它才能编码具有可解释性的变量。因此我们就有了z的不同维度，他们编码了不同的具有可解释性的变量。
    在人脸数据上训练的模型中，随着我们改变z1，从上往下看笑脸的程度在逐渐改变，从最上面的眉头紧锁到下面大的笑脸；接下来改变z2，从左往右看发现人脸的朝向在变化，从一个方向一直向另一个方向变化。

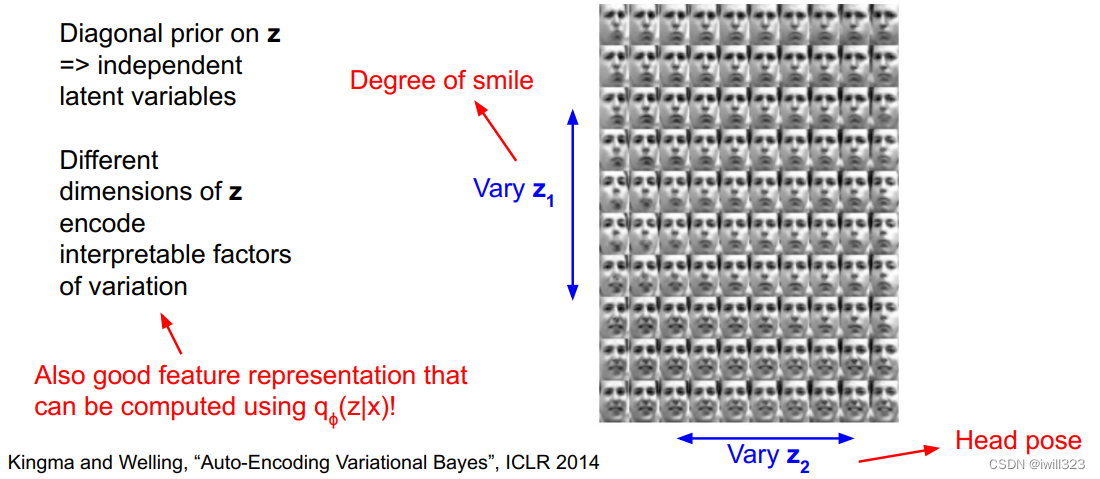
z同时也是很好的特征表示，因为z编码了这些不同的可解释语义的信息是多少。这样我们就可以利用q(z|x)也就是我们训练好的编码器，我们给他一个输入，将图像x映射到z，并把z用作下游任务的特征，比如监督学习，分类任务。 

 总结

在传统自编码器上加入了随机成分，输入不是确定的，而是随机采样

定义了一个难以计算的密度函数，推导出一个下边界并优化它

 Pros:
- Principled approach to generative models
- Interpretable latent space.
- Allows inference of q(z|x), can be useful feature representation for other tasks
Cons:
- Maximizes lower bound of likelihood: okay, but not as good evaluation as
PixelRNN/PixelCNN
- Samples blurrier and lower quality compared to state-of-the-art (GANs)
Active areas of research:
- More flexible approximations, e.g. richer approximate posterior instead of diagonal
Gaussian, e.g., Gaussian Mixture Models (GMMs), Categorical Distributions.
- Learning disentangled representations.
 

生成对抗网络GAN

GAN思路

一种隐式密度估计模型，放弃显式地对密度函数建模，而是从分布中采样并获得质量良好的样本。它解决了训练样本的分布维度高，难以采样的问题。其解决方法类似VAE，从一个简单的分布（比如符合高斯分布的随机噪声）中采样， 然后使用神经网络学习一种映射可以将其转变到训练样本的分布。

GAN定义了两个网络：生成器和判别器。

生成器负责利用随机噪声z生成假样本，它的职责是生成尽可能真的样本以骗过判别器。

判别器负责辨别哪些样本是生成器生成的假样本，哪些是从真实训练集中抽出来的真样本。

GAN的训练过程就是上面提到的两个玩家的博弈过程，即生成器网络和判别器网络。

将具有指定维度的随机噪声输入到生成器网络，生成器网络将会生成图片，即来自生成器的伪样本，然后从训练集中取一些真实图片，使用判别器网络对每个图片样本做出正确的区分，这是真实样本还是伪样本。训练过程就是让生成器不断提高“造假”能力，让判别器不断提高“鉴赏”能力。如果生成器骗过了判别器，那么我们就有了很好的生成模型

目标函数

mini max博弈公式

G表示生成网络，D 表示判别网络，θd​是判别器参数，θg​是生成器的参数，训练目标是让目标函数在θg​上取得最小值，同时在 θd​上取得最大值。

第一项：pdata 表示数据的分布。Dθd(x)是判别器网络对真实数据（训练数据）x的判别结果，输出一个 0-1 的概率（0表示假，1表示真）。E表示我们考虑的是整个训练集中所有样本的一个期望，而不是具体某个样本的概率。

第二项：p(z)表示噪声的分布。使用 Gθg(z) 可以生成一个样本，Dθd​​(Gθg​​(z))代表了判别器网路对生成的伪数据的判别结果。

θd的目标：整个表达式越大越好。希望E...logDθd(x) 越大越好，即判别器对于真实样本的判别为真的期望越大越好；希望 E...log(1−Dθd(Gθg(z)))越大越好，也就是希望判别器对假的样本判别为真的概率越小越好。因此如果能最大化这一结果，就意味着判别器能够很好的区别真实数据和伪造数据。

θg的目标：整个式子越小越好。想要整个式子越小，也就是让Dθd(Gθg(z))越大越好，也就是说希望生成器判别伪造样本为真的概率越大越好。最小化这一结果意味着生成器在生成与真实样本非常相似的数据

训练流程

首先对判别器进行梯度上升，学习到θd来最大化该目标函数，假设训练集中有1000张图片，那么我们就可以随机生成1000张图片，然后训练判别器使其能够区分这2000张图片即可；对生成器进行梯度下降，θg进行梯度下降最小化目标函数，此时目标函数只取右边这一项，因为只有这一项与θg有关。交替训练生成器和判别器，每次迭代生成器都试图骗过判别器。

 实际训练时，对于生成器的训练不会使用 梯度下降 和最小化的目标函数，如上图的蓝色曲线为 log(1−Dθd(Gθg(z)))。当生成器效果不好（D(G(z)接近0）时，梯度非常平缓，模型训练很慢；当生成器效果好（D(G(z)接近1）时，梯度很陡峭，模型更新地会过快，这也不是我们想看到的。这就与我们期望的相反了，我们希望在生成器效果不好的时候梯度更陡峭，这样能学到更多，在即将收敛的时候应该放缓更新步伐。

因此我们使用下面的目标函数来替代原来的生成器损失：

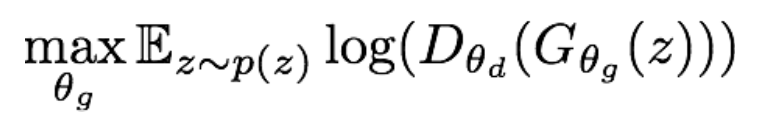
其图像如下图绿色曲线所示，它就有很好的特性，即初始时梯度大，最后梯度小，符合训练的需要，实际训练中基本都用这个式子。

 完整的训练过程：在每一个训练迭代期都先训练判别器网络，然后训练生成器网络。
    对于判别器网络的k个训练步，先从噪声先验分布z中采样得到一个小批量样本，接着从训练数据x中采样获得小批量的真实样本，将噪声样本传给生成器网络，并在生成器的输出端获得生成的图像。此时我们有了一个小批量伪造图像和小批量真实图像，在判别器生进行一次梯度计算，利用梯度信息更新判别器参数，按照以上步骤迭代几次来训练判别器。
    之后训练生成器，采样获得一个小批量噪声样本，将它传入生成器，对生成器进行反向传播，优化目标函数。

    交替进行上述两个步骤。

 训练完之后，将噪声图像传给生成网络，就能生成伪造图像

GAN的探索

传统的GAN生成的样本还不是很好，这篇论文在GAN中使用了CNN架构，取得了惊艳的生成效果： Radford et al, “Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks”, ICLR 2016

联合训练两个网络很有挑战。Wasserstein GAN 一定程度解决了GAN训练中两个网络如何平衡的问题

https://github.com/soumith/ganhacks
https://github.com/hindupuravinash/the-gan-zoo

 总结

Don’t work with an explicit density function
Take game-theoretic approach: learn to generate from training distribution through 2-player
game
Pros:
- Beautiful, state-of-the-art samples!
Cons:
- Trickier / more unstable to train
- Can’t solve inference queries such as p(x), p(z|x)
Active areas of research:
- Better loss functions, more stable training (Wasserstein GAN, LSGAN, many others)
- Conditional GANs, GANs for all kinds of applications

    GAN不使用显式的密度函数，而是利用样本来隐式表达该函数，GAN通过一种博弈的方法来训练，通过两个玩家的博弈从训练数据的分布中学会生成数据。

    GAN可以生成目前最好的样本，还可以做很多其他的事情。但是不好训练且不稳定，我们并不是直接优化目标函数，我们要努力地平衡两个网络。  
 

GAN：简单理解与实验生成对抗网络GAN_on2way的博客-CSDN博客_生成对抗网络

参考 cs231n---生成模型 - coldyan - 博客园

https://blog.csdn.net/qq_41533576/article/details/119717790【2017CS231n】第十三讲：生成模型（PixelRNN/PixelCNN，变分自编码器，生成对抗网络）_金刚哥葫芦娃的博客-CSDN博客https://blog.csdn.net/qq_41533576/article/details/119717790

CS231n：11 生成模型 - 腾讯云开发者社区-腾讯云

最后

以上就是丰富皮卡丘为你收集整理的CS231n 2022PPT笔记- 生成模型Generative Modeling概念生成模型分类 PixelRNN和PixelCNN Variational Autoencoders (VAE)生成对抗网络GAN的全部内容，希望文章能够帮你解决CS231n 2022PPT笔记- 生成模型Generative Modeling概念生成模型分类 PixelRNN和PixelCNN Variational Autoencoders (VAE)生成对抗网络GAN所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。