一、线性空间的同构:
一个集合V是否构成数域P的一个线性空间,主要看它是否定义了“加法”和“数乘”运算,以及这两种运算是否满足线性空间的八种运算规则。
定义1:数域P上的两个线性空间V1和V2称为是同构的,如果V1和V2之间存在一一对应关系σ,使得对于任意x,y属于V1使得λ属于P均满足:σ(x+y)=σ(x)+σ(y)、σ(λx)=λσ(x)称σ为V1到V2上的同构映射;
简单的理解:V1和V2称之为是同构的,如果这两者之间能建立起元素(向量)的一一对应关系,并且这个对应能够保持在V1中的加法和数乘运算。
数域P上每个n维线性空间V,当确定一组基的时候,V与Pm同构。(一种一一对应关系)


同构是有限维线性空间 ,其维数相同。
定理1:数域P上的两个n维线性空间V1和V2都是同构的。(维数相同)
推论:数域P上的两个有限维的线性空间同构的充要条件是维数相同。
二、线性变换的概念:
定义1:线性空间V的一个变换T称为线性变换。如果对于任意x,y属于V,以及λ属于数域P都满足一下条件:
1、T(x+y)=T(x)+T(y) 2、T(λx)=λT(x);(在变换T上满足加法和数乘的封闭运算,x和y均是向量)
由此定义可知,线性变换T是V->V的“保持向量加法”及“数乘”的变换。线性变换T的定义也可以描述为:若T是V到V的映射,x,y是V中的任意元素,λ属于数域P的任意元素,如果在T的作用下x->x',y->y',则有x+y->x'+y',λx->λx'。在这里称T(x)或x'为向量x在线性变换T下的象,x叫做T(x)或x'的原象。在这里约定V的任意两个线性变换T与S认为是相等的,即T(x)=S(x)
在线性空间V中的每一个向量都映射到零向量的变换称为0变换,反之映射到自身的变换称为单位变换。这里的0变换和单位变换都是线性变换。(线性变换的例子:多项式求导、多项式的不定积分,矩阵运算等)
线性变换的性质:1、T(0)=0;2、T(-x)=-T(x);
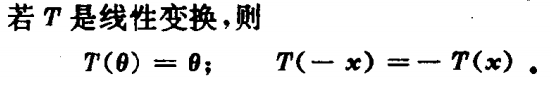
设V是数域P上的线性空间,T1、T2、T3是V的三种线性变换,在此基础上定义三种运算:(基本运算)
1)线性变换的和:对于任意x属于V,则满足 T(x)=T1(x)+T2(x),变换T称为线性变换T1和T2的和,记做T=T1+T2;
2)线性变换的乘积:对于任意x属于V,则满足T(x)=T1(T2(x)),变换T称为线性变换T1和T2的乘积,记做T=T1*T2;
线性变换的和以及乘积仍然是线性变换。
3)线性变换的数量乘法:对于任意x属于V,λ属于数域P,满足T(x)=λ(T1(x)),变换T称为数λ与线性变换T1的数量乘法,记做T=λT1;
线性变换T1、T2、T3对于结合律成立:T1*(T2*T3)=(T1*T2)*T3;结合律
线性空间V中的线性变换的加法满足交换律以及结合律;
线性空间V中线性变换的乘法对于加法的分配律成立。
线性空间V中的零变换O以及任意线性变换T,均满足:T+O=T、T+(-T)=O;
数量乘法满足一下关系式:(对于这里的a和b属于数域P,T1和T2以及T均为V的任意线性变换)
| (a+b)T=aT+bT; |
| (ab)T=a(bT); |
| a(T1+T2)=aT1+aT2; |
| 1T=T; |
定理:I为线性空间V中的单位线性变换,T为V的线性变换,如果存在一个V的线性变换S使得:TS=ST=I成立,则称线性变换T是可逆的,S称为T的逆变换,记做T^-1;(如矩阵类似,并非每个线性变换都是可逆的)
三、线性变换的矩阵表示:
定理:V为数域P上的n维线性空间,a1,a2....,an为线性空间V的一组基,又b1,b2...,bn是V的任意n个向量,则存在唯一的线性变换T,使得 T(ai)=bi (i为小于等于n的自然数)
在这里(Ta1,Ta2....Tan)=(a1,a2,...an)A;A为线性变换T在基(a1,a2,...,an)下的矩阵;
同理我们可以定义(Tb1,Tb2....Tbn)=(b1,b2,...bn)B;T在基(b1.b2,...bn)下的矩阵;
(Tb1,Tb2....Tbn)=T(b1,b2,...bn),由两组基的过渡矩阵可得出,T(b1,b2,...bn)=T(a1,a2,...an)P
已知(Ta1,Ta2....Tan)=T(a1,a2,...an)=(a1,a2,...an)A;带入上式中,得(Tb1,Tb2....Tbn)=(a1,a2,...an)AP
在由(b1.b2,...bn)=(a1,a2,...,an)P得出(a1,a2,...,an)=(b1.b2,...bn)P^-1,与上式联立得出
(Tb1,Tb2....Tbn)=(b1.b2,...bn)P^-1AP,得出T在基(b1.b2,...bn)下的矩阵B=P^-1AP;
定义:A,B属于P^n*n,存在可逆矩阵P,使得B=P^-1AP则称A相似于B
性质:相似具有自反性、对称性、传递性;
最后
以上就是发嗲毛豆最近收集整理的关于矩阵分析学习(二)的全部内容,更多相关矩阵分析学习(二)内容请搜索靠谱客的其他文章。








发表评论 取消回复