poj1651矩阵连乘问题

矩阵连乘，通过加括号来决定计算优先级，从而得到计算(只计算乘法）的最小次数。

输入：输入n，n-1个矩阵相乘，需要n列数。然后输入n个数xi。

输出：n个矩阵相乘最后得到的最小计算次数

算法思想：

假设矩阵有A1、A2、.....An个，

则我们从简单的开始计算，即每两个矩阵都计算它们需要的计算次数。

然后再计算每3个矩阵需要计算的次数，这时候，根据最优子结构性质，

在得出每3个矩阵次数的时候，结合最优的2个矩阵的计算次数。

例如 ,  矩阵(行，列)     A1(10,1)，A2(1,50)，A3(50,50) 

则首先计算每两个的计算次数，A1*A2 = 10*1*50 =500，A2*A3 = 1*50*50 = 2500

然后计算A1*A2*A3这时候有两种方案 

(A1*A2)*A3 = (10*1*50)*50*50 = 1250000    

A1*(A2*A3) = 10*1*(1*50*50) = 25000

明显选择第二种方案。

如图，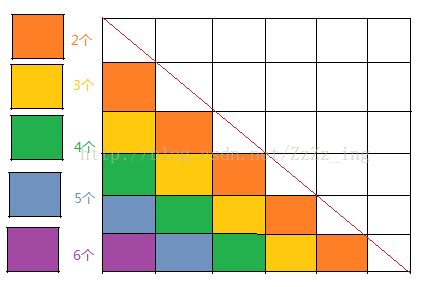

因此，子问题有两个矩阵相乘一直到n-1(所有)个矩阵相乘，就是我们需要的答案。

从表格图上来看，我们可以得到紫色方块就是我们要的最终解。

#include<iostream>
#include<cstdio>
#define INF 99999999
using namespace std;
int sum[102][102];  //将所有可能组合的计算次数存储起来
int x[102];   //代表行列
int n;    //代表矩阵数目n-1
void calculate()
{
	memset(sum, 0, sizeof(sum));

	for (int len = 1;len < n;++len)  //len代表与之矩阵的个数，len=1为有2个矩阵相乘
	{
		for (int i = 1, j = len + 1;j < n;++i, ++j)
		{
			int min = INF;
			for (int k = i;  k < j;++k)
			{
				/*
					sum[i][k]代表前k-i(0代表矩阵自身，计算次数为0)个矩阵的最小计算次数
					sum[k+1][j]代表后面矩阵的最小计算次数
					x[i-1]*x[k]*x[j]代表两边矩阵计算后结果的矩阵的相乘的次数
				*/
				int tempsum = sum[i][k] + sum[k + 1][j] + x[i - 1] * x[k] * x[j];
				if (min > tempsum)
					min = tempsum;//选出最小值，得到最终结果
			}
			sum[i][j] = min;
		}
	}
}
int main()
{
	while (cin >> n)
	{
		for (int i = 0;i < n;++i)
			cin >> x[i];

		calculate();   //计算矩阵计算需要的次数
		cout << sum[1][n - 1] << endl;//输出最终结果
	}
}

最后

以上就是潇洒黑裤为你收集整理的poj1651矩阵连乘问题的全部内容，希望文章能够帮你解决poj1651矩阵连乘问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。