概述
初级算法 - 数组篇完结：
初级算法 - 数组(一)：
https://blog.csdn.net/weixin_43854928/article/details/121315702
初级算法 - 数组(二)：
https://blog.csdn.net/weixin_43854928/article/details/121523946
初级算法 - 数组(三)：
https://blog.csdn.net/weixin_43854928/article/details/121568562
目录
- 1. 两数之和
- 36. 有效的数独
- 48. 旋转图像
1. 两数之和
给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个
整数，并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1：
输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] = 9 ，返回 [0, 1] 。
示例 2：
输入：nums = [3,2,4], target = 6 输出：[1,2]
链接：https://leetcode-cn.com/problems/two-sum
思路：
最开始的思路是先把数据做一个简单的筛选：建立一个新的数组，只存放小于和的数据，之后对这个数组做简单的双层for查找，查找到两个值以后，再做两遍单层for找到两个数据在原数组中的位置并返回。
时间复杂度在O(n²/4) ~ O(n²)之间(因为多了两个for)。
结果审题不清，数据是可以有负数的，倒在了这条用例下：
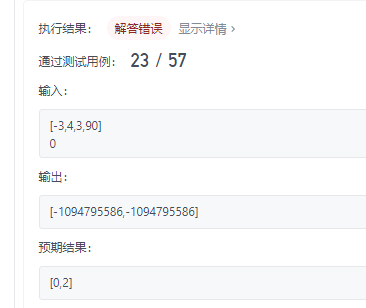
气急败坏直接暴力破解：
int* twoSum(int* nums, int numsSize, int target, int* returnSize)
{
int* ret_buf = (int*)malloc(2*sizeof(int));
for(int i=0; i<numsSize-1; i++)
{
for(int j=i+1; j<numsSize; j++)
{
if(nums[i]+nums[j] == target)
{
ret_buf[0] = i;
ret_buf[1] = j;
}
}
}
*returnSize = 2;
return ret_buf;
}
当然暴力破解的时间复杂度就很难看了，妥妥的O(n²)
最后还是hashmap解决：从头遍历到尾，每到一个元素时检查对应的差值元素是否在hashmap中，存在的话直接获取到下标并结束，不存在的话把自己添加到hashmap中。
这里注意：在hashmap的节点中增加了index成员变量，向表中添加元素时把下标也一起添加进去，存在的话就可以直接返回下标而不是再根据值遍历数组，也是空间换时间了。
时间复杂度O(n)
struct hash_node
{
char flag;
int number;
int index;
struct hash_node* next;
};
void add_hash_node(int data_num, int numsSize, int index, struct hash_node* hash_map)
{
int key = (data_num&0x7FFFFFFF)%numsSize;
struct hash_node* node = &hash_map[key];
struct hash_node* next_node = node;
do
{
node = next_node;
if(!node->flag)//空
{
node->number = data_num;
node->index = index;
node->flag = 1;
return ;
}
next_node = node->next;
}
while(next_node);
node->next = calloc(1, sizeof(struct hash_node));
node->next->number = data_num;
node->next->index = index;
node->next->flag = 1;
return;
}
int find_hash_node(int data_num, int numsSize, struct hash_node* hash_map)
{
int key = (data_num&0x7FFFFFFF)%numsSize;
struct hash_node* node = &hash_map[key];
struct hash_node* next_node = node;
do
{
node = next_node;
if(node->flag)//非空
{
if(node->number == data_num)
{
return node->index;
}
}
next_node = node->next;
}
while(next_node);
return -1;
}
void free_hash_node(struct hash_node* hash_map)
{
if(hash_map->next != NULL)
{
free_hash_node(hash_map->next);
}
else
{
free(hash_map);
}
}
void free_hash_map(struct hash_node* hash_map, int map_size)
{
for(int i = 0; i<map_size; i++)
{
if(hash_map[i].next!= NULL)
{
free_hash_node(hash_map[i].next);
}
}
free(hash_map);
}
int* twoSum(int* nums, int numsSize, int target, int* returnSize)
{
int* ret_buf = (int*)malloc(2*sizeof(int));
int* hash_map = (int*)calloc(numsSize, sizeof(struct hash_node));
for(int i=0; i<numsSize; i++)
{
int hash_find = find_hash_node(target-nums[i], numsSize, hash_map);
if(hash_find >= 0)
{
ret_buf[0] = hash_find;
ret_buf[1] = i;
}
else
{
add_hash_node(nums[i], numsSize, i, hash_map);
}
}
free_hash_map(hash_map, numsSize);
*returnSize = 2;
return ret_buf;
}
最后还加了一个hashmap的释放函数，不然就内存泄漏了，分两步：1. 把所有线性表上额外添加的链表节点，通过递归的方式释放掉。2. 把整个malloc的线性表释放掉。
36. 有效的数独
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3宫内只能出现一次。（请参考示例图）
注意：
一个有效的数独（部分已被填充）不一定是可解的。 只需要根据以上规则，验证已经填入的数字是否有效即可。
空白格用 ‘.’ 表示。
示例1：
输入：board = [[“5”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”]
,[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”]
,[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”]
,[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”]
,[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”]
,[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”]
,[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”]
,[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”]
,[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
输出：true
链接：https://leetcode-cn.com/problems/valid-sudoku
思路：
先暴力破解法:
横、竖、方格三个函数各自遍历一遍表格，data[9]数组的下标对应表格中出现的数据值，如果出现了一次置为1，出现第二次时return false;
横竖比较简单，主要是方格，思路是把9*9的81个方格，转换成3*3的9个方格，编号是0~8，每个方格有9个元素，方格内就可以按照与横竖中相同的处理办法使用data[9]数组做判断了。
方法是把
行号/3*3(0、1、2->0, 3、4、5->3, 6、7、8->6) + 列号/3(0、1、2->0, 3、4、5->1, 6、7、8->2),
得数作为一个9*9的二维数组的行号索引，从而让每个3*3的方格找到自己对应的"data[9]"。
bool horizontally(char** board)
{
for(int i=0; i<9; i++)
{
char data[9] = {0};
for(int j=0; j<9; j++)
{
if(board[i][j] != '.')
{
if(data[board[i][j]-'1'] == 1)
{
return false;
}
else
{
data[board[i][j]-'1'] = 1;
}
}
}
}
return true;
}
bool vertically(char** board)
{
for(int i=0; i<9; i++)
{
char data[9] = {0};
for(int j=0; j<9; j++)
{
if(board[j][i] != '.')
{
if(data[board[j][i]-'1'] == 1)
{
return false;
}
else
{
data[board[j][i]-'1'] = 1;
}
}
}
}
return true;
}
bool square(char** board)
{
char data[9][9] = {0};
for(int i=0; i<9; i++)
{
for(int j=0; j<9; j++)
{
if(board[i][j] != '.')
{
if(data[(i/3)*3 + j/3][board[i][j]-'1'] == 1)
{
return false;
}
else
{
data[(i/3)*3 + j/3][board[i][j]-'1'] = 1;
}
}
}
}
return true;
}
bool isValidSudoku(char** board, int boardSize, int* boardColSize)
{
if(!horizontally(board) || !vertically(board) || !square(board))
{
return false;
}
return true;
}
进一步把算法做优化:
把行、列、方格三个函数合成一个，这样执行一遍遍历即可完成所有的对比。注意：因为是按行遍历，所以保存列的遍历状态的数组需要从一维换成二维。
bool isValidSudoku(char** board, int boardSize, int* boardColSize)
{
short vertically_data[9] = {0};
short square_data[9] = {0};
for(int i=0; i<9; i++)
{
short horizontally_data = 0;
for(int j=0; j<9; j++)
{
char char_data = board[i][j];
if(char_data != '.')
{
short bit_data = 0x01<<(char_data-'1');
if((horizontally_data & bit_data) || (vertically_data[j] & bit_data) || (square_data[(i/3)*3 + j/3] & bit_data))
{
return false;
}
else
{
horizontally_data |= bit_data;
vertically_data[j] |= bit_data;
square_data[(i/3)*3 + j/3] |= bit_data;
}
}
}
}
return true;
}
再进一步优化的话应该可以把所有的data[9]数组用一个char替换，对应索引的元素运算换成索引对应的位运算，内存能减少。意义不是很大了没有继续做。
48. 旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1：
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]
链接：https://leetcode-cn.com/problems/rotate-image
思路：
提高执行效率的思路是同一个元素不要操作两遍，甚至是不能遍历到第二遍。
因为是旋转90°，不是180°或者镜像，因此如果按行遍历的方法一定会有元素被重复遍历。
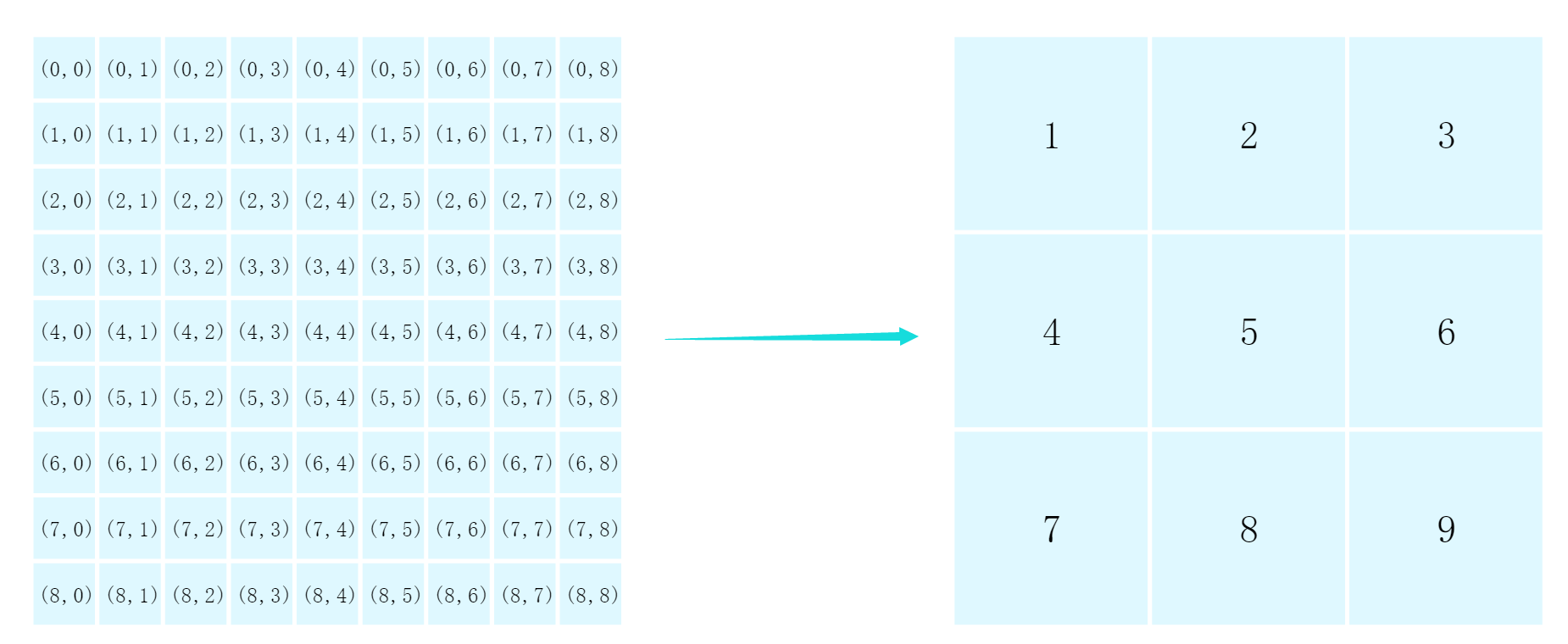
因此方法是把数组按照对角线连线，分成四个部分，四个部分按箭头方向替换：
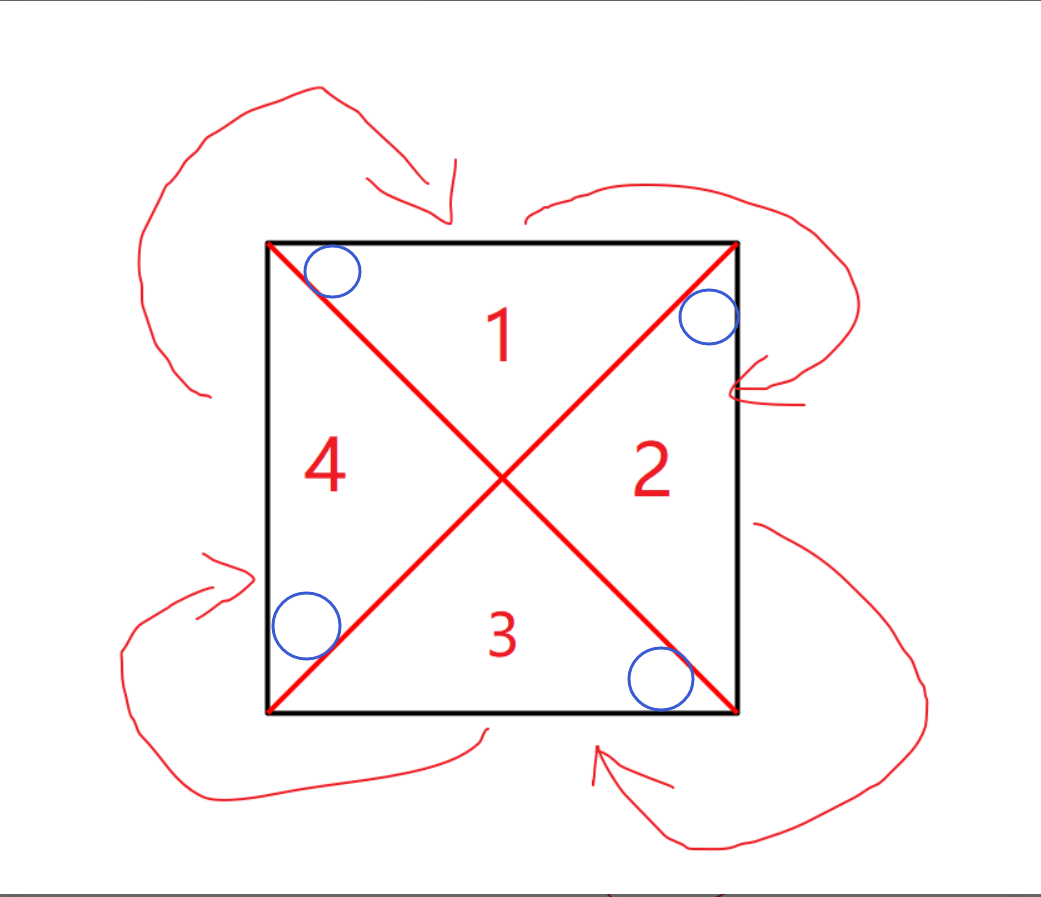
遍历块1，然后找到块1中的元素在块2、3、4中对应的位置并进行交换。
void rotate(int** matrix, int matrixSize, int* matrixColSize)
{
for(char i = 0; i<matrixSize/2; i++)
{
for(char j = i; j<matrixSize-i-1; j++)
{
short buf = matrix[i][j];
matrix[i][j] = matrix[matrixSize-j-1][i];
matrix[matrixSize-j-1][i] = matrix[matrixSize-i-1][matrixSize-j-1];
matrix[matrixSize-i-1][matrixSize-j-1] = matrix[j][matrixSize-i-1];
matrix[j][matrixSize-i-1] = buf;
}
}
}
数组篇完结
最后
以上就是鳗鱼戒指为你收集整理的[算法]力扣刷题-初级算法 - 数组(三)(数组篇完结) [两数之和] [有效的数独] [旋转图像]的全部内容，希望文章能够帮你解决[算法]力扣刷题-初级算法 - 数组(三)(数组篇完结) [两数之和] [有效的数独] [旋转图像]所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
![[算法]力扣刷题-初级算法 - 数组(三)(数组篇完结) [两数之和] [有效的数独] [旋转图像]](/uploads/reation/bcimg4.png)
发表评论 取消回复