复数矩阵和快速傅里叶变换

90 阅读 0 评论 60 点赞

我是靠谱客的博主生动胡萝卜，最近开发中收集的这篇文章主要介绍复数矩阵和快速傅里叶变换，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

有时实矩阵会有复数的特征值，当特征值变成复数时，特征向量也会变成复数，傅里叶矩阵是复矩阵里最重要的例子。先来讨论一般的复向量和复矩阵，如果给定复向量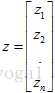，则其不再属于Rⁿ，而属于n维复空间Cⁿ，z中每个元素都是复数，此时在实数空间中定义的向量求模方法：z^T乘z将不再适用，因为模长的平方应该始终是正数，在复数空间，z的模长平方应该等于z1的共轭乘以z1加上z2的共轭乘以z2一直加到zn的共轭乘以zn，即z的模长的平方应该是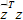，这个式子说明在求复向量的模长时不仅要做转置，还要求共轭，用符号H表示这两个操作同时做，这个H代表Hermite，即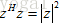。除了模长，在实数中定义的向量内积同样不再适用，两个复向量的内积不再是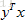，这是对实数而言的，对于复向量，不仅要转置，而且要取共轭，即两复向量的内积为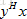，当然结果也不再是实数了，大部分情况下内积结果也是复数。除了模长和内积，对称矩阵在复数空间也需要重新定义，不再是A^T=A，而是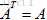，这才是对复数矩阵适用的对称性，并且在复数空间中这些也不再称为对称阵，而是称为Hermitian矩阵，即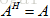，前面的博文推导过实数空间中对称阵的特征值为实数，且特征向量相互垂直，对于Hermitian矩阵这些结论同样成立，假设其有相互垂直的复向量q1,q2,…,qn，这些向量都是其标准正交基，垂直意味着qi和qj的内积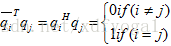，现构造矩阵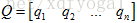，与实数空间中类比一下，则有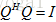，这里的Q也不再称为正交矩阵（orthogonal matrix），而是称为酉矩阵（unitary matrix），使用不一样的名称代表我们处理的是复矩阵，酉矩阵和正交矩阵很相似，它是n阶方阵，列向量正交。

接下来介绍最著名的复数矩阵---傅里叶矩阵，它也是酉矩阵，即有正交的列向量。n阶傅里叶矩阵的形式如下：

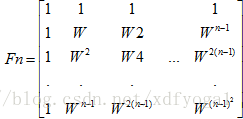
傅里叶矩阵中的每个元素都是某个数W的幂，从上面的形式中可看出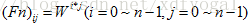，W不是随便取，而是要满足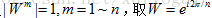，在复平面内，W落在单位圆上，因为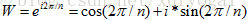。W落在单位圆上，且其幅角就是一整圈的1/n，比如说n=6，则其幅角为pi/3，W²,W³…W⁵,W⁶也在单位圆上，对应的幅角相应每次增加60°，如下图所示。

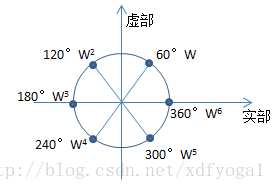
W,W²,W³…W⁵,W⁶是1的6次方根，而W又称为原根；如果n=4，此时W的4次方等于1，则有原根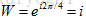，从而可写出1的所有四次方根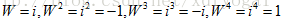：，并可写出4阶傅里叶矩阵为：

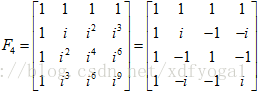
正如前面已指出的那样，我们不难发现幂指数的规律：指数等于行序数乘以列序数，行、列序数都从0开始，通常这个4阶傅里叶矩阵可得到一个4维序列（有4个离散点）的傅里叶变换（离散的），矩阵F4左乘4维向量得到该向量的傅里叶变换，F4^-1左乘4维向量的傅里叶变换则得该向量。F4是各列正交的，但不是标准正交向量，只要修正一下，列向量的长度等于2，除以该系数，则矩阵各列变成标准正交向量，则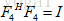，这样就很容易求其逆。那么是什么导致了快速傅里叶变换FFT的问世呢？根据傅里叶矩阵的定义，容易看出F6和F3，F8和F4 ，F64和F32等等这些矩阵之间存在某种奇妙的联系，F64是一个64阶方阵，W是1的64次方根，F32是一个32阶方阵，W是1的32次方根，容易理解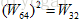，如果直接用F64乘以一个列向量，则一般的情况下总共需要64²次数值乘法，而如果将F64分解成如下的形式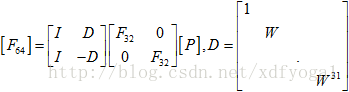：，其中P是32维置换矩阵，用于将向量中的奇偶行分开，比如说4维的置换阵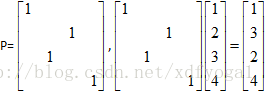，将F64分解成上面的形式后，不再需要64²的乘法，首先在上面的分解式中，无论乘以I还是乘以P都不需要大量开销，因为计算机可以在瞬间完成，因此主要的开销是耗在F32以及D上，2个F32只需要2*32²次乘法，再加上由乘以对角阵D带来的32 次数值乘法（虽然有两个D，但是两次结果只有符号不同，因此开销只需一个D的数值乘法），最终计算开销由64²变成2*32²，如果将F32继续分解成F16甚至继续向下分解，则开销会变得越来越小，最终达到n/2*log2(n)，即64/2*log2(64)，这就是使用快速傅里叶变换带来的好处。