概述
特殊矩阵的主要形式有：
（1）对称矩阵
（2）上三角矩阵／下三角矩阵
（3）对角矩阵
它们都是方阵，即行数和列数相同。
一、对称矩阵的压缩存储
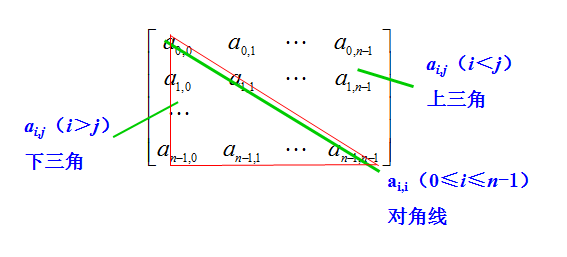
若一个n阶方阵A[n][n]中的元素满足a i,j=a j,i（0≤i，j≤n-1），则称其为n阶对称矩阵。
由于对称矩阵中的元素关于主对角线对称，因此在存储时可只存储对称矩阵中上三角或下三角中的元素，使得对称的元素共享一个存储空间。
这样，就可以将n2个元素压缩存储到n(n+1)/2个元素的空间中。以行序为主序存储其下三角＋对角线的元素。
n2个元素←→ n(n+1)/2个元素
A[0..n-1,0..n-1] ←→ B[0..n(n+1)/2-1]
a[i][j] ←→ b[k]
二、三角矩阵的压缩存储
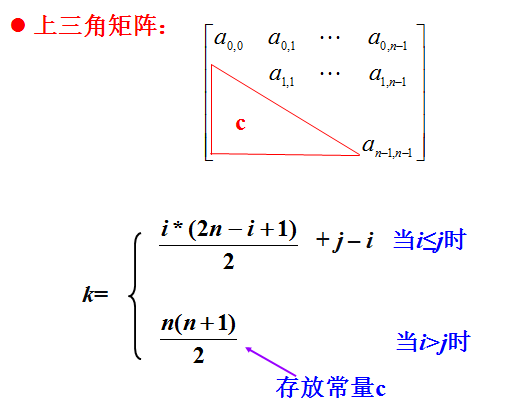
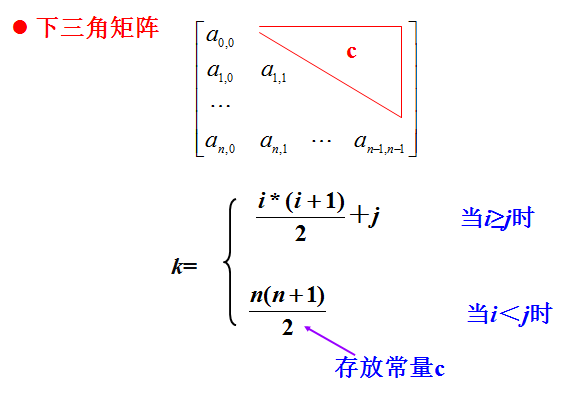
三、 对角矩阵的压缩存储
若一个n阶方阵A满足其
所有非零元素
都集中在以主对角线为中心的
带状区域中
，则称其为
n阶对角矩阵
。
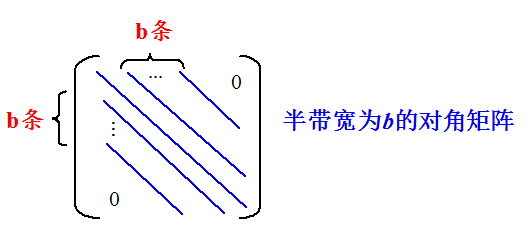
其主对角线上下方各有b条次对角线，称b为矩阵半带宽，(2b+1)为矩阵的带宽。
对于半带宽为b（0≤b≤(n-1)/2）的对角矩阵，其|i-j|≤b的元素ai,j不为零，其余元素为零。
下图所示是半带宽为b的对角矩阵示意图。
A ←→ B
a[i][j] ←→ b[k]
当b＝1时称为三对角矩阵。其压缩地址计算公式如下： k=2i+j
最后
以上就是故意世界为你收集整理的特殊矩阵的压缩存储的全部内容，希望文章能够帮你解决特殊矩阵的压缩存储所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复