矩阵快速幂---斐波那契数列

62 阅读 0 评论 41 点赞

我是靠谱客的博主鲜艳枕头，最近开发中收集的这篇文章主要介绍矩阵快速幂---斐波那契数列，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

先来实现一个矩阵相乘的函数吧。

const int MOD=10000;
struct mat
{
    int a[2][2];//这里数据范围就用小的示范
};
mat mat_mul(mat x,mat y)//实现两个矩阵相乘，返回的还是一个矩阵。
{
    mat res;//用来表示得到的新的矩阵；
    memset(res.a,0,sizeof(res.a));
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
        for(int k=0;k<2;k++)
    {
        res.a[i][j]+=x.a[i][k]*y.a[k][j];
        res.a[i][j]%=MOD;//这一步看题目具体需要了
    }
    return res;
}

矩阵快速幂

//其实和普通快速幂类似，只不过这里需要得到的是一个矩阵

下面来实现一个矩阵快速幂：

int pow(int n)//还是小范围数据来说吧,要不然返回值的类型自己定义
{
    mat c,res;
    memset(res.a,0,sizeof(res.a));
    c.a[0][0]=1;//给矩阵赋初值
    c.a[0][1]=1;
    c.a[1][0]=1;
    c.a[1][1]=0;
    for(int i=0;i<n;i++) res.a[i][i]=1;//单位矩阵；
    while(n)
    {
        if(n&1) res=mat_mul(res,c);//这里看就要用到上面的矩阵相乘了；
        c=mat_mul(c,c);
        n=n>>1;
    }
    return res.a[0][1];
}//时间复杂度log(n)

但是矩阵如何与斐波那契联系在一起呢？？？

对于矩阵乘法与递推式之间的关系：

如：在斐波那契数列之中

f[i] = 1*f[i-1]+1*f[i-2] f[i-1] = 1*f[i-1] + 0*f[i-2];

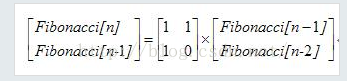
所以

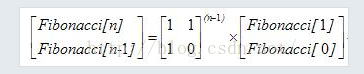
就这两幅图完美诠释了斐波那契数列如何用矩阵来实现。

下面一POJ3070/NYOJ148为例

给出了矩阵相乘的定义，要你求出斐波那契的第n项对1e4取余。（实际上就是求其第n项的后四位数）

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD=10000;
struct mat
{
    ll a[2][2];
};
mat mat_mul(mat x,mat y)
{
    mat res;
    memset(res.a,0,sizeof(res.a));
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
        for(int k=0;k<2;k++)
        res.a[i][j]=(res.a[i][j]+x.a[i][k]*y.a[k][j])%MOD;
    return res;
}
void mat_pow(int n)
{
    mat c,res;
    c.a[0][0]=c.a[0][1]=c.a[1][0]=1;
    c.a[1][1]=0;
    memset(res.a,0,sizeof(res.a));
    for(int i=0;i<2;i++) res.a[i][i]=1;
    while(n)
    {
        if(n&1) res=mat_mul(res,c);
        c=mat_mul(c,c);
        n=n>>1;
    }
    printf("%I64dn",res.a[0][1]);
    //至于为什么返回res.a[0][1]请看前面的图解
}
int main()
{
    int n;
    while(~scanf("%d",&n)&&n!=-1)
    {
        mat_pow(n);
    }
    return 0;
}