矩阵快速幂与递推式

其实矩阵快速幂和快速幂取模在实质上是相同的，通过在幂指数的那部分快速幂，减少了时间复杂度。

在这里就不详细说明了，直接给出代码：

#include<stdio.h>
#include<string.h>
#define NN 2
typedef long long ll; 
struct matrix  //设定为NN*NN的矩阵 
{
    ll mat[NN][NN];
};
matrix mutiplymat(matrix a,matrix b)
{
    matrix c;
    memset(c.mat,0,sizeof(c.mat));
    for(ll i=0;i<NN;i++)          //矩阵乘法 
        for(ll k=0;k<NN;k++)
            for(ll j=0;j<NN;j++)
                c.mat[i][j]=(c.mat[i][j]+(a.mat[i][k]%m)*(b.mat[k][j]%m))%m;
    return c;
}
matrix powerm(matrix a,ll b)
{
    matrix ans;
    for(ll i=0;i<NN;i++)
    {
        for(ll j=0;j<NN;j++)
        {
            if(i==j) ans.mat[i][j]=1;
            else ans.mat[i][j]=0;
        }
    }
    while(b>0)           //矩阵快速幂 
    {
        if(b%2==1)ans=mutiplymat(ans,a);
        a=mutiplymat(a,a);
		b>>=1;
    }
    return ans;
}

对于含有递推式的数列，其运算都是需要一步步递推（或递归）来进行第n项值的计算，然而这样时间复杂度为O（n），对于较大的n的运算就很难在短时间实现了。

于是就产生了利用矩阵快速幂来进行递推式项的运算。

首先来看这个矩阵乘法

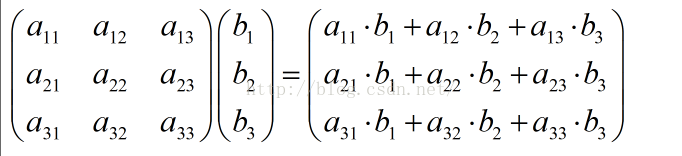
通过这个乘法法则，我们可以得出矩阵关于递推式的乘法（例如菲波那切数列 F(n)=F(n-1)+F(n-2)）：

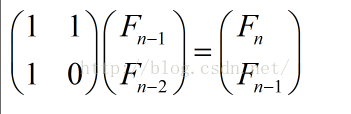
再例如F(n)=2*F(n-1)+1：

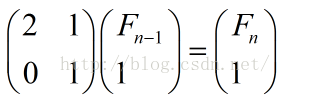
通过以上的分析，我们就可以通过 递推式→矩阵相乘式 的转换，从而实现递推式项的运算。

但是时间复杂度还没有降下来，于是我们就想到利用矩阵快速幂，来提高矩阵幂次运算的效率。

对于这种类型的题目，难点在于构造矩阵，之后就是套模板的事儿了。

最后

以上就是冷静蜜粉为你收集整理的矩阵快速幂与递推式的全部内容，希望文章能够帮你解决矩阵快速幂与递推式所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。