矩阵快速幂和递推式构造常矩阵总结

前言

今天学长讲了矩阵快速幂，说着是这周最简单的一个知识点，可我听了一遍还是不知道怎么搞的；为什么线性代数不早点学呢，真的不知道学院怎么安排课程的，身为一个计算机学科的学生，竟然到大二下学期才学线代…昨天的背包可能背背模板就完事了，今天的矩阵也可以称作是模板吧，但是应用的时候还是挺难的我感觉，尤其是让你自己分析递推式然后构造矩阵，没有头绪，今晚就想到啥总结啥吧，以后陆续再更新；
先把模板亮出来吧，以简单的斐波那契数列的求法举个栗子：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
 using namespace std;
 typedef long long ll;
 const int mod=1e4;
struct node
{
    ll ma[5][5];//用来存放矩阵的数组
};
 int n;
 node mul(node a,node b)//矩阵的乘法
 {
     node ans;
     memset(ans.ma,0,sizeof ans.ma);//每一次都要将矩阵清空为0
    for(int i=1;i<=2;i++)
        for(int j=1;j<=2;j++)
         for(int k=1;k<=2;k++)
            ans.ma[i][j]=(ans.ma[i][j]+a.ma[i][k]*b.ma[k][j])%mod;//关键步骤，矩阵的相乘法则
    return ans;
 }
 node pow(node a,int b)//矩阵的快速幂
 {
     node ans;
     memset(ans.ma,0,sizeof ans.ma);//每一次都要将矩阵清空为0
     for(int i=1;i<=2;i++) ans.ma[i][i]=1;
     while(b)
     {
         if(b&1) ans=mul(ans,a);
         a=mul(a,a);
         b>>=1;
     }
     return ans;
 }
 int main()
 {
     int n;
     while(cin >>n)
     {
         if(n==-1) break;
         node a,ans,b;
         a.ma[1][1]=1,a.ma[1][2]=1;//这个是构造的矩阵
         a.ma[2][1]=1,a.ma[2][2]=0;
//         b.ma[1][1]=1,b.ma[1][2]=1;
//         b.ma[2][1]=0,b.ma[2][2]=1;
         ans=pow(a,n);
         cout <<ans.ma[2][1]<<endl;
     }
     return 0;
 }

1

首先了解一下矩阵的乘法：戳一戳

知道两个矩阵相乘的时候每行每列是怎么样搞得是第一步；
然后要知道普通常数的快速幂模板是啥：戳一戳

2

矩阵快速幂是啥，有啥用？
借助一个例题来说一下：
戳一戳：1113 矩阵快速幂
这就是直接了当的求矩阵的n次幂，直接套用模板就行；

3

矩阵快速幂的应用
比如上面举的例子，求斐波那契的第n项，当然可以直接的用递推循环来求第n项的值，甚至去打表，但如果求得是第10^18次方项呢；用循环测评机会气死，那么矩阵快速幂就登场了；

第一步就是找到递推式，然后构造常数矩阵；怎样构造常数矩阵，推荐一篇写的特别好
戳一戳根据递推公式构造系数矩阵用于快速幂
其次最重要的就是判断要把这个常数矩阵进行几次幂运算，这就需要一步一歩看矩阵的递推过程中常数矩阵要被重复几次了；
例如斐波那契：

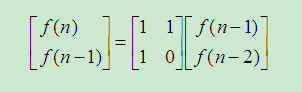
然后进行递推直到出现最小的竖型矩阵

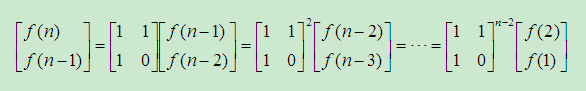
4

要把An=T^n-1*A1中的A1这个矩阵求出来，然后再与前面的快速幂矩阵相乘，就得出来fn。此时fn如图在[ 1 ] [ 1 ]的位置，有时候不一样，要根据矩阵递推式来判断要求的fn在矩阵的那个位置；

最后

以上就是寒冷纸飞机为你收集整理的矩阵快速幂和递推式构造常矩阵总结的全部内容，希望文章能够帮你解决矩阵快速幂和递推式构造常矩阵总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。