递推数列 矩阵快速幂

https://www.nowcoder.com/practice/d0e751eac618463bb6ac447369e4aa25?tpId=40&tqId=21352&rp=1&ru=/ta/kaoyan&qru=/ta/kaoyan/question-ranking
给定a0,a1,以及an=p*a(n-1) + q*a(n-2)中的p,q。这里n >= 2。 求第k个数对10000的模。

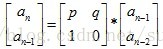
推得

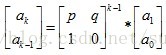
矩阵快速幂

#include <iostream>
#include <cstdio>
using namespace std;

const int MOD=10000;
void Matrix_mul(int p[2][2], int q[2][2])
{
    int i, j, k;
    int t[2][2]= {0};
    for(i = 0; i <= 1; i++)
        for(j = 0; j <= 1; j++)
            for(k = 0; k <= 1; k++)
                t[i][j] += p[i][k] * q[k][j];
    for(i = 0; i <= 1; i++)
        for(j = 0; j <= 1; j++)
            p[i][j] = t[i][j] % MOD;
}

/*计算p矩阵的n次方，结果存入p矩阵*/
void Matrix_cal(int p[2][2], int n)
{
    int i, j;
    int t[2][2];
    for(i = 0; i <= 1; i++)
        for(j = 0; j <= 1; j++)
            t[i][j] = p[i][j];
    if(n == 1)
        return;
    else if(n & 1)
    {
        Matrix_cal(p, n-1);
        Matrix_mul(p, t);
    }
    else
    {
        Matrix_cal(p, n/2);
        Matrix_mul(p, p);
    }
}

int main()
{
    int a0, a1, p, q, k;
    while(scanf("%d%d%d%d%d", &a0, &a1, &p, &q, &k) != EOF)
    {
        if(k == 0)
            printf("%dn", a0);
        else if(k == 1)
            printf("%dn", a1);
        else
        {
            int matrix[2][2] = { {p%MOD, q%MOD}, {1, 0} };
            Matrix_cal(matrix, k-1);
            printf("%dn", (a1 * matrix[0][0] + a0 * matrix[0][1]) % MOD);
        }
    }
    return 0;
}

最后

以上就是飘逸裙子最近收集整理的关于递推数列 矩阵快速幂的全部内容，更多相关递推数列内容请搜索靠谱客的其他文章。