洛谷 P1939 【模板】矩阵加速（数列）：优化递推式的方法——矩阵快速幂

在大多数情况下，O(n)的效率都是值得骄傲的，然而，有时候并不是，比如如何在一秒钟内算出一个递推式的第1e9项，很明显O(n)不行了。

然而常数级又不太现实，除非你的数学非常好，这题又比较简单，你推了一个特征方程的通项公式……

所以考虑log的做法：矩阵快速幂

如果你还不知道矩阵快速幂是什么，请走这边：传送门

对于这道题，嗯，模板嘛，已经告诉你了式子，就只需要考虑矩阵了，对于整个过程，我们只需要两个矩阵，初始矩阵和转置矩阵：

先看这个特征方程F[i] = F[i - 1] + F[i - 3]，那么就有一个矩阵如下

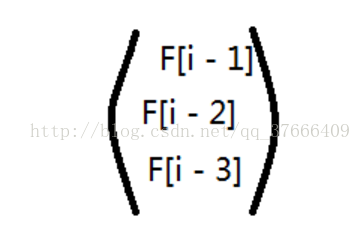
我们的目标矩阵就是

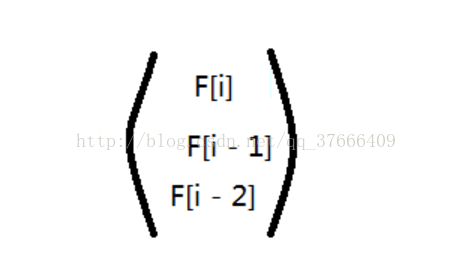
那么，针对这个矩阵我们如何转置呢？

先看目标矩阵第一个：F[i]

F[i] = F[i - 1] + F[i - 3]

那么，由矩阵乘法，转置矩阵第一行，似乎就定了：1 0 1

同样的，二三行就是1 0 0 和 0 1 0

整个矩阵如下：

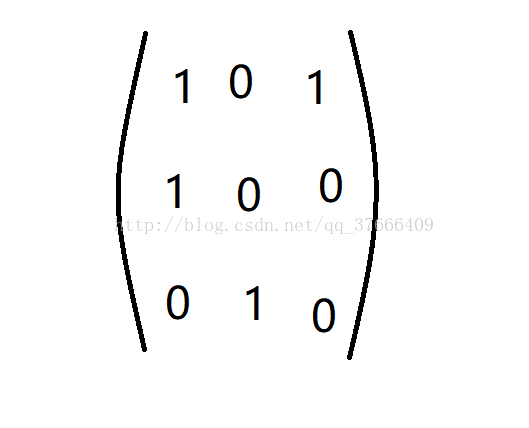
代码：

#include <bits/stdc++.h>
const int mod = 1000000007;
int n;
inline int read()
{
    int ch;int x = 0;int f = 1;ch=getchar();
    while (ch!='-'&&(ch<'0'||ch>'9'))
        ch=getchar();
    ch=='-'?f=-1:x=ch-'0',ch=getchar();
     while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
     return x*f;
}
struct Mat {
    long long mat[3][3];
};
Mat operator * (Mat a, Mat b) {
    Mat c;
    memset(c.mat, 0, sizeof(c.mat));
    for(int i = 0; i < 3; i++) {
        for(int k = 0; k < 3; k++) {
            for(int j = 0; j < 3; j++) {
                c.mat[i][j] += (a.mat[i][k] % mod) * (b.mat[k][j] % mod) % mod;
                c.mat[i][j] %= mod;
            }
        }
    }
    return c;
}
Mat operator ^ (Mat a, long long k)  {
    Mat c;
    for(int i = 0; i < 3; i++)
        for(int j = 0; j < 3; j++) c.mat[i][j] = (i == j);
    while(k) {
        if(k & 1) c = c * a;
        a = a * a;
        k >>= 1;
    }
    return c;
}
Mat init;
Mat fi;
int t;
signed main()
{
    scanf("%d", &t);
    while(t--)
    {
        memset(init.mat, 0, sizeof(init.mat));
        memset(fi.mat, 0, sizeof(fi.mat));
        scanf("%d", &n);
        init.mat[0][0] = 1;
        init.mat[0][2] = 1;
        init.mat[1][0] = 1;
        init.mat[2][1] = 1;
        fi.mat[0][0] = 1;
        fi.mat[1][0] = 1;
        fi.mat[2][0] = 1;
        if(n <= 3) printf("%dn", 1);
        else{
            init = init ^ (n - 3);
            fi = init * fi;
            printf("%dn", fi.mat[0][0]);
        }
    }
    return 0;
}

最后

以上就是老迟到月亮为你收集整理的洛谷 P1939 【模板】矩阵加速（数列）：优化递推式的方法——矩阵快速幂的全部内容，希望文章能够帮你解决洛谷 P1939 【模板】矩阵加速（数列）：优化递推式的方法——矩阵快速幂所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。