矩阵快速幂（大斐波那契数）

矩阵快速幂就是把快速幂的乘法变成矩阵乘法。

应用：求斐波那契数取模（大数）

斐波那契数列递推公式（这里取从第二项开始）：f(1)=1，f(2)=2，f(n)=f(n-1)+f(n-2)(n>=3)

 用矩阵表示为：

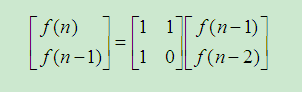
进一步，可以得出直接推导公式：

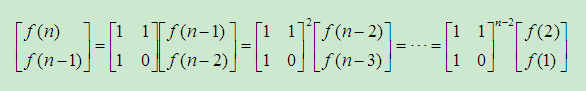
求第n项斐波那契数就是求

1 1
1 0的（n-1）次方的第一行第一列项，也就是n次方的第一行第二列项

#include<bits/stdc++.h>
using namespace std;

const int maxn=2;//阶数 
const int mod=100007;

//矩阵结构体 
struct ma//matrix矩阵 
{
    int a[maxn][maxn];
    void init()
	{    //初始化为单位矩阵 
        memset(a,0,sizeof(a));
        for(int i=0;i<maxn;++i) a[i][i] = 1;
    }
};

//矩阵乘法 
ma mul(ma a, ma b)
{
    ma ans;
    for(int i=0;i<maxn;++i)
	{
        for(int j=0;j<maxn;++j)
		{
            ans.a[i][j] = 0;
            for(int k=0;k<maxn;++k)
			{
                ans.a[i][j]+=a.a[i][k]*b.a[k][j];
                ans.a[i][j]%=mod; 
            }
        }
    } 
    return ans;
}

//矩阵快速幂 
ma qpow(ma a,int n)
{
    ma ans;
    ans.init();
    while(n)
	{
        if(n&1) ans=mul(ans,a);
        a=mul(a,a);
        n/=2;
    } 
    return ans;
}

void output(ma a)
{
    for(int i=0;i<maxn;++i)
	{
        for(int j=0;j<maxn;++j) cout<<a.a[i][j]<<" ";
        cout<<endl;
    }
}

int main()
{
	int n;
    ma a;
    a.a[0][0]=1;
    a.a[0][1]=1;
    a.a[1][0]=1;
    a.a[1][1]=0;
    cin>>n;
    ma ans=qpow(a,n); 
    output(ans);//第n个矩阵 
    cout<<ans.a[0][1];//第n个斐波那契数 
    return 0;
}

最后

以上就是鲤鱼帅哥为你收集整理的矩阵快速幂（大斐波那契数）的全部内容，希望文章能够帮你解决矩阵快速幂（大斐波那契数）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。