矩阵上的动态规划
- 本期题目:
- 下降最小路径和
- 最小路径和
- 三角形最小路径和
- 地下城游戏
- 最大正方形
- 矩阵中的最长递增路径
最小路径和问题
我们先来看三道最小路径和问题
问题描述: 给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
实际上,我们可以把状态就定义成在矩阵中的位置,在某一时刻如果在位置 ( i , j ) (i,j) (i,j)中,那么下一步要么走到 ( i + 1 , j ) (i+1,j) (i+1,j),要么都走到 ( i , j + 1 ) (i,j+1) (i,j+1),然后再分别从 ( i + 1 , j ) (i+1,j) (i+1,j)和 ( i , j + 1 ) (i,j+1) (i,j+1)走到终点 ( m − 1 , n − 1 ) (m-1,n-1) (m−1,n−1)两者分别都取一条路径和最小的最优路径,接上 ( i , j ) (i,j) (i,j),就得到 ( i , j ) (i,j) (i,j)到终点 ( m − 1 , n − 1 ) (m-1,n-1) (m−1,n−1)的两条路径,两条路径中路径和最小的就是 ( i , j ) (i,j) (i,j)到 ( m − 1 , n − 1 ) (m-1,n-1) (m−1,n−1)的最优路径,定义dp矩阵为 d p [ i ] [ j ] dp[i][j] dp[i][j]为从 ( i , j ) (i,j) (i,j)走到终点 ( m − 1 , n − 1 ) (m-1,n-1) (m−1,n−1)的最小路径和。 g ( i , j ) = { min ( d p [ i + 1 ] [ j ] , d p [ i ] [ j + 1 ] ) i < n − 1 , j < m − 1 d p [ i + 1 ] [ j ] i < n − 1 , j = m − 1 d p [ i ] [ j + 1 ] i = n − 1 , j < m − 1 0 i = n − 1 , j = m − 1 d p [ i ] [ j ] = g r i d [ i ] [ j ] + g ( i , j ) begin{aligned} &g(i,j)=begin{cases} min(dp[i+1][j],dp[i][j+1])&i<n-1,j<m-1\ dp[i+1][j]&i<n-1,j=m-1\ dp[i][j+1]&i=n-1,j<m-1\ 0&i=n-1,j=m-1 end{cases}\ &dp[i][j]=grid[i][j]+g(i,j) end{aligned} g(i,j)=⎩⎪⎪⎪⎨⎪⎪⎪⎧min(dp[i+1][j],dp[i][j+1])dp[i+1][j]dp[i][j+1]0i<n−1,j<m−1i<n−1,j=m−1i=n−1,j<m−1i=n−1,j=m−1dp[i][j]=grid[i][j]+g(i,j)
这样就可以进行动态规划,时间复杂度是 O ( n m ) O(nm) O(nm),由于每次状态转移都只需要用到 d p [ i + 1 ] [ j ] dp[i+1][j] dp[i+1][j]和 d p [ i ] [ j + 1 ] dp[i][j+1] dp[i][j+1],因此可以做一个一维的dp数组即可,空间复杂度可以降低至 O ( m i n ( n , m ) ) O(min(n,m)) O(min(n,m))
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
if(n==1){
int sum=0;
for(const auto&a:grid[0]){
sum+=a;
}
return sum;
}else if(m==1){
int sum=0;
for(int i=0;i<n;i++){
sum+=grid[i][0];
}
return sum;
}else if(m<n){
vector<int> dp(m,0);
dp[m-1] = grid[n-1][m-1];
for(int i=m-2;i>=0;i--){
dp[i]=dp[i+1]+grid[n-1][i];
}
for(int i=n-2;i>=0;i--){
dp[m-1]+=grid[i][m-1];
for(int j=m-2;j>=0;j--){
dp[j]=((dp[j]<dp[j+1])?dp[j]:dp[j+1])+grid[i][j];
}
}
return dp[0];
}else{
vector<int> dp(n,0);
dp[n-1] = grid[n-1][m-1];
for(int i=n-2;i>=0;i--){
dp[i]=dp[i+1]+grid[i][m-1];
}
for(int j=m-2;j>=0;j--){
dp[n-1]+=grid[n-1][j];
for(int i=n-2;i>=0;i--){
dp[i]=((dp[i]<dp[i+1])?dp[i]:dp[i+1])+grid[i][j];
}
}
return dp[0];
}
}
};
复杂度分析: 时间复杂度 O ( n m ) O(nm) O(nm),空间复杂度 O ( min ( n , m ) ) O(min(n,m)) O(min(n,m))
Leetcode成绩:执行用时:8 ms, 在所有 C++ 提交中击败了77.77% 的用户,内存消耗:9.5 MB, 在所有 C++ 提交中击败了74.31% 的用户
另外两道最小路径和问题也是类似的,这里直接给出C++代码
最小下降路径和
问题描述: 给你一个n x n的方形整数数组matrix,请你找出并返回通过matrix的下降路径的最小和 。
下降路径可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。具体来说,位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& matrix) {
int n=matrix.size();
if(n==1) return matrix[0][0];
else if(n==2) return min(matrix[0][0],matrix[0][1])+min(matrix[1][0],matrix[1][1]);
else{
vector<int> dp(n,0);
//初始化
for(int i=0;i<n;i++) dp[i]=matrix[n-1][i];
//中间n-2次dp
for(int i=n-2;i>=1;i--){
int l=dp[0];
int r=dp[1];
dp[0]=matrix[i][0]+min(dp[0],dp[1]);
for(int j=1;j<=n-2;j++){
dp[j]=matrix[i][j]+min(l,min(r,dp[j+1]));
l=r;
r=dp[j+1];
}
dp[n-1]=matrix[i][n-1]+min(l,r);
}
//最后一次dp
int minFPS = min(matrix[0][0]+min(dp[0],dp[1]),matrix[0][n-1]+min(dp[n-2],dp[n-1]));
for(int i=1;i<=n-2;i++){
minFPS=min(minFPS,matrix[0][i]+min(dp[i-1],min(dp[i],dp[i+1])));
}
return minFPS;
}
}
};
复杂度分析: 时间复杂度 O ( n 2 ) O(n^2) O(n2),空间复杂度 O ( n ) O(n) O(n)
Leetcode成绩: 执行用时:4 ms, 在所有 C++ 提交中击败了99.95% 的用户,内存消耗:9.6 MB, 在所有 C++ 提交中击败了74.23% 的用户
三角形最小路径和
问题描述: 给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
int n=triangle.size();
if(n==1) return triangle[0][0];
else{
vector<int> dp(n,0);
//初始化
for(int i=0;i<n;i++) dp[i]=triangle[n-1][i];
//动态规划
for(int m=n-1;m>=1;m--){
for(int i=0;i<m;i++){
dp[i]=triangle[m-1][i]+min(dp[i],dp[i+1]);
}
}
return dp[0];
}
}
};
复杂度分析: 时间复杂度 O ( n 2 ) O(n^2) O(n2),空间复杂度 O ( n ) O(n) O(n)
Leetcode成绩: 执行用时:4 ms, 在所有 C++ 提交中击败了93.49% 的用户,内存消耗:8.5 MB, 在所有 C++ 提交中击败了42.95% 的用户
地下城游戏
三道最小路径和都可以表述成一个统一的最优化问题的形式,用
p
p
p来表示一个具体的坐标,
p
i
p_i
pi表示
i
i
i时刻所处的坐标,
f
(
p
i
)
f(p_i)
f(pi)表示
p
i
p_i
pi位置的矩阵的数字,
p
1
,
p
2
,
⋯
,
p
n
p_1,p_2,cdots,p_n
p1,p2,⋯,pn是一条路径
τ
tau
τ,它是合法的当且仅当
p
i
p_i
pi可以转移到
p
i
+
1
p_{i+1}
pi+1(
i
=
1
,
⋯
,
n
−
1
i=1,cdots,n-1
i=1,⋯,n−1),
τ
tau
τ合法我们记为
τ
p
.
p
.
tauquad p.p.
τp.p.,最小和问题都可以表述成选择一条路径和最小的合法路径,在最小路径和问题中,路径长度都是
n
+
m
−
1
n+m-1
n+m−1,在下降路径和问题中,路径长度都为
n
n
n,在三角形路径和问题中,路径长度都是
n
n
n。
min
p
1
,
⋯
,
p
N
p
.
p
.
∑
i
=
1
N
f
(
p
i
)
min_{p_1,cdots,p_N quad p.p.}sum_{i=1}^Nf(p_i)
p1,⋯,pNp.p.mini=1∑Nf(pi)
以最小路径和问题为例,
N
=
n
+
m
−
1
N=n+m-1
N=n+m−1,对于任意一条合法路径,
p
1
=
(
0
,
0
)
p_1=(0,0)
p1=(0,0),所以
min
p
1
,
⋯
,
p
N
p
.
p
.
∑
i
=
1
N
f
(
p
i
)
=
min
p
1
=
(
0
,
0
)
,
p
2
,
⋯
,
p
N
p
.
p
.
∑
i
=
1
N
f
(
p
i
)
=
f
(
0
,
0
)
+
min
p
1
=
(
0
,
0
)
,
p
2
,
⋯
,
p
N
p
.
p
.
∑
i
=
2
N
f
(
p
i
)
begin{aligned} &min_{p_1,cdots,p_N quad p.p.}sum_{i=1}^Nf(p_i)=min_{p_1=(0,0),p_2,cdots,p_Nquad p.p.}sum_{i=1}^Nf(p_i)\ =&f(0,0)+min_{p_1=(0,0),p_2,cdots,p_Nquad p.p.}sum_{i=2}^Nf(p_i) end{aligned}
=p1,⋯,pNp.p.mini=1∑Nf(pi)=p1=(0,0),p2,⋯,pNp.p.mini=1∑Nf(pi)f(0,0)+p1=(0,0),p2,⋯,pNp.p.mini=2∑Nf(pi)
由于在
p
1
=
(
0
,
0
)
p_1=(0,0)
p1=(0,0)情况下,
p
2
p_2
p2只有两种情况,
(
1
,
0
)
(1,0)
(1,0)或
(
0
,
1
)
(0,1)
(0,1),所以
min
p
1
=
(
0
,
0
)
,
p
2
,
⋯
,
p
N
p
.
p
.
∑
i
=
2
N
f
(
p
i
)
=
min
(
min
p
2
=
(
0
,
1
)
,
⋯
,
p
N
p
.
p
.
∑
i
=
2
N
f
(
p
i
)
,
min
p
2
=
(
1
,
0
)
,
⋯
,
p
N
p
.
p
.
∑
i
=
2
N
f
(
p
i
)
)
begin{aligned} &min_{p_1=(0,0),p_2,cdots,p_Nquad p.p.}sum_{i=2}^Nf(p_i)\=&min(min_{p_2=(0,1),cdots,p_Nquad p.p.}sum_{i=2}^Nf(p_i),min_{p_2=(1,0),cdots,p_Nquad p.p.}sum_{i=2}^Nf(p_i)) end{aligned}
=p1=(0,0),p2,⋯,pNp.p.mini=2∑Nf(pi)min(p2=(0,1),⋯,pNp.p.mini=2∑Nf(pi),p2=(1,0),⋯,pNp.p.mini=2∑Nf(pi))
所以
min
p
1
,
⋯
,
p
N
p
.
p
.
∑
i
=
1
N
f
(
p
i
)
=
f
(
0
,
0
)
+
min
p
1
=
(
0
,
0
)
,
p
2
,
⋯
,
p
N
p
.
p
.
∑
i
=
2
N
f
(
p
i
)
=
f
(
0
,
0
)
+
min
(
min
p
2
=
(
0
,
1
)
,
⋯
,
p
N
p
.
p
.
∑
i
=
2
N
f
(
p
i
)
,
min
p
2
=
(
1
,
0
)
,
⋯
,
p
N
p
.
p
.
∑
i
=
2
N
f
(
p
i
)
)
begin{aligned} &min_{p_1,cdots,p_N quad p.p.}sum_{i=1}^Nf(p_i)=f(0,0)+min_{p_1=(0,0),p_2,cdots,p_Nquad p.p.}sum_{i=2}^Nf(p_i)\ =&f(0,0)+min(min_{p_2=(0,1),cdots,p_Nquad p.p.}sum_{i=2}^Nf(p_i),min_{p_2=(1,0),cdots,p_Nquad p.p.}sum_{i=2}^Nf(p_i)) end{aligned}
=p1,⋯,pNp.p.mini=1∑Nf(pi)=f(0,0)+p1=(0,0),p2,⋯,pNp.p.mini=2∑Nf(pi)f(0,0)+min(p2=(0,1),⋯,pNp.p.mini=2∑Nf(pi),p2=(1,0),⋯,pNp.p.mini=2∑Nf(pi))这就是最小路径和的状态转移方程。这种推导看起来很多余,但是遇到更复杂的问题时,我们很难直观地找出状态转移方程,此时转化成最优化问题并且加以必要的数学推导能帮助我们得到准确的状态转移方程,一个典型的例子就是下面的地下城游戏。
地下城游戏
问题描述: 一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快到达公主,骑士决定每次只向右或向下移动一步。
编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。
我们先看看如果走某条具体的路径,需要的最低初始血量是多少?假设初始血量为0,走某条路径血量变化如下
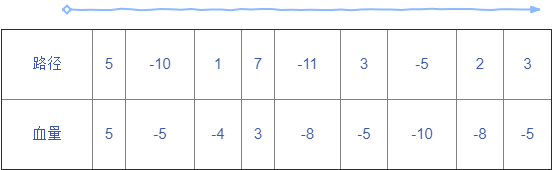
显然所需的最低血量是(1-最低血量),也就是11滴血,当然,如果是以下的路径:
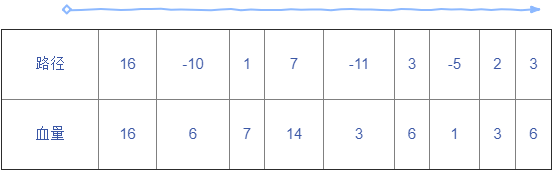
这样即便是零血量开局,后来也不会死亡,所以只需要开局有1滴血即可
所以,最低需要的血量为:
1
−
min
(
min
i
=
1
,
⋯
,
N
∑
j
=
1
i
f
(
p
j
)
,
0
)
1-minleft(min_{i=1,cdots,N}sum_{j=1}^if(p_j),0right)
1−min(i=1,⋯,Nminj=1∑if(pj),0)优化问题可以表述为
min
p
1
,
⋯
,
p
N
p
.
p
.
(
1
−
min
(
min
i
=
1
,
⋯
,
N
∑
j
=
1
i
f
(
p
j
)
,
0
)
)
=
1
−
max
p
1
,
⋯
,
p
N
p
.
p
.
min
(
min
i
=
1
,
⋯
,
N
∑
j
=
1
i
f
(
p
j
)
,
0
)
=
1
−
min
(
max
p
1
,
⋯
,
p
N
p
.
p
.
min
i
=
1
,
⋯
,
N
∑
j
=
1
i
f
(
p
j
)
,
0
)
begin{aligned} &min_{p_1,cdots,p_Nquad p.p.}left(1-minleft(min_{i=1,cdots,N}sum_{j=1}^if(p_j),0right)right)\ =&1-max_{p_1,cdots,p_Nquad p.p.}minleft(min_{i=1,cdots,N}sum_{j=1}^if(p_j),0right)\ =&1-minleft(max_{p_1,cdots,p_Nquad p.p.}min_{i=1,cdots,N}sum_{j=1}^if(p_j),0right) end{aligned}
==p1,⋯,pNp.p.min(1−min(i=1,⋯,Nminj=1∑if(pj),0))1−p1,⋯,pNp.p.maxmin(i=1,⋯,Nminj=1∑if(pj),0)1−min(p1,⋯,pNp.p.maxi=1,⋯,Nminj=1∑if(pj),0)因此问题转化成
max
p
1
,
⋯
,
p
N
p
.
p
.
min
i
=
1
,
⋯
,
N
∑
j
=
1
i
f
(
p
j
)
max_{p_1,cdots,p_Nquad p.p.}min_{i=1,cdots,N}sum_{j=1}^if(p_j)
p1,⋯,pNp.p.maxi=1,⋯,Nminj=1∑if(pj)假设
p
1
=
p
1
(
0
)
p_1=p_1^{(0)}
p1=p1(0)是给定的,定义
g
(
p
1
(
0
)
)
=
max
p
1
=
p
1
(
0
)
,
p
2
,
⋯
,
p
N
p
.
p
.
min
i
=
1
,
⋯
,
N
∑
j
=
1
i
f
(
p
j
)
g(p_1^{(0)})=max_{p_1=p_1^{(0)},p_2,cdots,p_Nquad p.p.}min_{i=1,cdots,N}sum_{j=1}^if(p_j)
g(p1(0))=p1=p1(0),p2,⋯,pNp.p.maxi=1,⋯,Nminj=1∑if(pj)
于是
g
(
p
1
(
0
)
)
=
max
p
1
=
p
1
(
0
)
,
p
2
,
⋯
,
p
N
p
.
p
.
min
(
f
(
p
1
(
0
)
)
,
min
i
=
2
,
⋯
,
N
∑
j
=
1
i
f
(
p
j
)
)
=
max
p
1
=
p
1
(
0
)
,
p
2
,
⋯
,
p
N
p
.
p
.
min
(
f
(
p
1
(
0
)
)
,
min
i
=
2
,
⋯
,
N
(
f
(
p
1
(
0
)
)
+
∑
j
=
2
i
f
(
p
j
)
)
)
=
max
p
1
=
p
1
(
0
)
,
p
2
,
⋯
,
p
N
p
.
p
.
min
(
f
(
p
1
(
0
)
)
,
f
(
p
1
(
0
)
)
+
min
i
=
2
,
⋯
,
N
(
∑
j
=
2
i
f
(
p
j
)
)
)
=
f
(
p
1
(
0
)
)
+
max
p
1
=
p
1
(
0
)
,
p
2
,
⋯
,
p
N
p
.
p
.
min
(
0
,
min
i
=
2
,
⋯
,
N
(
∑
j
=
2
N
f
(
p
j
)
)
)
=
f
(
p
1
(
0
)
)
+
min
(
0
,
max
p
1
=
p
1
(
0
)
,
p
2
,
⋯
,
p
N
p
.
p
.
min
i
=
2
,
⋅
,
N
∑
j
=
2
N
f
(
p
j
)
)
begin{aligned} g(p_1^{(0)})=&max_{p_1=p_1^{(0)},p_2,cdots,p_Nquad p.p.}minleft(f(p_1^{(0)}),min_{i=2,cdots,N}sum_{j=1}^if(p_j)right)\ =&max_{p_1=p_1^{(0)},p_2,cdots,p_Nquad p.p.}minleft(f(p_1^{(0)}),min_{i=2,cdots,N}left(f(p_1^{(0)})+sum_{j=2}^if(p_j)right)right)\ =&max_{p_1=p_1^{(0)},p_2,cdots,p_Nquad p.p.}minleft(f(p_1^{(0)}),f(p_1^{(0)})+min_{i=2,cdots,N}left(sum_{j=2}^if(p_j)right)right)\ =&f(p_1^{(0)})+max_{p_1=p_1^{(0)},p_2,cdots,p_Nquad p.p.}minleft(0,min_{i=2,cdots,N}left(sum_{j=2}^Nf(p_j)right)right)\ =&f(p_1^{(0)})+minleft(0,max_{p_1=p_1^{(0)},p_2,cdots,p_Nquad p.p.}min_{i=2,cdot,N}sum_{j=2}^Nf(p_j)right) end{aligned}
g(p1(0))=====p1=p1(0),p2,⋯,pNp.p.maxmin(f(p1(0)),i=2,⋯,Nminj=1∑if(pj))p1=p1(0),p2,⋯,pNp.p.maxmin(f(p1(0)),i=2,⋯,Nmin(f(p1(0))+j=2∑if(pj)))p1=p1(0),p2,⋯,pNp.p.maxmin(f(p1(0)),f(p1(0))+i=2,⋯,Nmin(j=2∑if(pj)))f(p1(0))+p1=p1(0),p2,⋯,pNp.p.maxmin(0,i=2,⋯,Nmin(j=2∑Nf(pj)))f(p1(0))+min(0,p1=p1(0),p2,⋯,pNp.p.maxi=2,⋅,Nminj=2∑Nf(pj))假设
p
1
(
0
)
p_1^{(0)}
p1(0)不在最后一行,也不在最后一列,那么可以向右走,也可以向下走,设向右走可以走到
p
2
′
p_2^prime
p2′,向下走可以走到
p
2
′
′
p_2^{primeprime}
p2′′,那么
max
p
1
=
p
1
(
0
)
,
p
2
,
⋯
,
p
N
p
.
p
.
min
i
=
2
,
⋅
,
N
∑
j
=
2
N
f
(
p
j
)
=
max
(
max
p
2
=
p
2
′
,
⋯
,
p
N
p
.
p
.
min
i
=
2
,
⋅
,
N
∑
j
=
2
N
f
(
p
j
)
,
max
p
2
=
p
2
′
′
,
⋯
,
p
N
p
.
p
.
min
i
=
2
,
⋅
,
N
∑
j
=
2
N
f
(
p
j
)
)
=
max
(
g
(
p
2
′
)
,
g
(
p
2
′
′
)
)
begin{aligned} &max_{p_1=p_1^{(0)},p_2,cdots,p_Nquad p.p.}min_{i=2,cdot,N}sum_{j=2}^Nf(p_j)\ =&maxleft(max_{p_2=p_2^prime,cdots,p_Nquad p.p.}min_{i=2,cdot,N}sum_{j=2}^Nf(p_j),max_{p_2=p_2^{primeprime},cdots,p_Nquad p.p.}min_{i=2,cdot,N}sum_{j=2}^Nf(p_j)right)\ =&max(g(p_2^prime),g(p_2^{primeprime})) end{aligned}
==p1=p1(0),p2,⋯,pNp.p.maxi=2,⋅,Nminj=2∑Nf(pj)max(p2=p2′,⋯,pNp.p.maxi=2,⋅,Nminj=2∑Nf(pj),p2=p2′′,⋯,pNp.p.maxi=2,⋅,Nminj=2∑Nf(pj))max(g(p2′),g(p2′′))所以,就有状态转移方程
g
(
p
1
(
0
)
)
=
f
(
p
1
(
0
)
)
+
min
(
0
,
max
(
g
(
p
2
′
)
,
g
(
p
2
′
′
)
)
)
g(p_1^{(0)})=f(p_1^{(0)})+minleft(0,maxleft(g(p_2^primeright),g(p_2^{primeprime}))right)
g(p1(0))=f(p1(0))+min(0,max(g(p2′),g(p2′′)))
如果在最后一行或最后一列,则下一步只有一种走法,设只能走到
p
2
′
p_2^prime
p2′,则状态转移方程为
g
(
p
1
(
0
)
)
=
f
(
p
1
(
0
)
)
+
min
(
0
,
g
(
p
2
′
)
)
g(p_1^{(0)})=f(p_1^{(0)})+minleft(0,g(p_2^prime)right)
g(p1(0))=f(p1(0))+min(0,g(p2′))
通过一系列的数学推导,可以得到状态转移方程
d
p
[
i
]
[
j
]
=
{
d
u
n
g
e
o
n
[
i
]
[
j
]
+
min
(
0
,
max
(
d
p
[
i
+
1
]
[
j
]
,
d
p
[
i
]
[
j
+
1
]
)
)
i
<
n
−
1
,
j
<
m
−
1
d
u
n
g
e
o
n
[
i
]
[
j
]
+
min
(
0
,
d
p
[
i
+
1
]
[
j
]
)
i
<
n
−
1
,
j
=
m
−
1
d
u
n
g
e
o
n
[
i
]
[
j
]
+
min
(
0
,
d
p
[
i
]
[
j
+
1
]
)
i
=
n
−
1
,
j
<
m
−
1
d
u
n
g
e
o
n
[
n
−
1
]
[
m
−
1
]
i
=
n
−
1
,
j
=
m
−
1
begin{aligned} &dp[i][j]=\ &begin{cases} dungeon[i][j]+min(0,max(dp[i+1][j],dp[i][j+1]))&i<n-1,j<m-1\ dungeon[i][j]+min(0,dp[i+1][j])&i<n-1,j=m-1\ dungeon[i][j]+min(0,dp[i][j+1])&i=n-1,j<m-1\ dungeon[n-1][m-1]&i=n-1,j=m-1 end{cases} end{aligned}
dp[i][j]=⎩⎪⎪⎪⎨⎪⎪⎪⎧dungeon[i][j]+min(0,max(dp[i+1][j],dp[i][j+1]))dungeon[i][j]+min(0,dp[i+1][j])dungeon[i][j]+min(0,dp[i][j+1])dungeon[n−1][m−1]i<n−1,j<m−1i<n−1,j=m−1i=n−1,j<m−1i=n−1,j=m−1然后再返回
1
−
m
i
n
(
0
,
d
p
[
0
]
[
0
]
)
1-min(0,dp[0][0])
1−min(0,dp[0][0]),并且从状态转移方程可以看出空间复杂度可以降至
O
(
min
(
n
,
m
)
)
O(min(n,m))
O(min(n,m)),时间复杂度为
O
(
n
m
)
O(nm)
O(nm),C++代码如下:
class Solution {
public:
int calculateMinimumHP(vector<vector<int>>& dungeon) {
int n=dungeon.size();
int m=dungeon[0].size();
if(n==1){//边界条件,只有一行,只能一直向右走
int l1=dungeon[0][0];
int minl1=dungeon[0][0];
for(int j=1;j<m;j++){
l1+=dungeon[0][j];
minl1=min(minl1,l1);
}
return (minl1>=0)?1:(1-minl1);
}else if(m==1){//边界条件,只有一列,只能一直向下走
int l1=dungeon[0][0];
int minl1=dungeon[0][0];
for(int i=1;i<n;i++){
l1+=dungeon[i][0];
minl1=min(minl1,l1);
}
return (minl1>=0)?1:(1-minl1);
}else if(n>m){//内存优化版本
vector<int> dp(m,0);
//最后一列初始化
dp[m-1]=dungeon[n-1][m-1];
for(int j=m-2;j>=0;j--){
dp[j]=dungeon[n-1][j]+min(0,dp[j+1]);
}
//前面几列依次dp
for(int i=n-2;i>=0;i--){
dp[m-1]=dungeon[i][m-1]+min(0,dp[m-1]);
for(int j=m-2;j>=0;j--){
dp[j]=dungeon[i][j]+min(0,max(dp[j+1],dp[j]));
}
}
return (dp[0]>=0)?1:(1-dp[0]);
}else{
vector<int> dp(n,0);
//最后一行初始化
dp[n-1]=dungeon[n-1][m-1];
for(int i=n-2;i>=0;i--){
dp[i]=dungeon[i][m-1]+min(0,dp[i+1]);
}
//前面几行依次dp
for(int j=m-2;j>=0;j--){
dp[n-1]=dungeon[n-1][j]+min(0,dp[n-1]);
for(int i=n-2;i>=0;i--){
dp[i]=dungeon[i][j]+min(0,max(dp[i+1],dp[i]));
}
}
return (dp[0]>=0)?1:(1-dp[0]);
}
}
};
复杂度分析: 时间复杂度 O ( n m ) O(nm) O(nm),空间复杂度 O ( min ( n , m ) ) O(min(n,m)) O(min(n,m))
Leetcode成绩: 执行用时:4 ms, 在所有 C++ 提交中击败了94.38% 的用户,内存消耗:8.6 MB, 在所有 C++ 提交中击败了82.07% 的用户
最大正方形
问题描述: 在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积。
假设
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j]是以
(
i
,
j
)
(i,j)
(i,j)为左上顶点的最大正方形的边长,那么,问题的答案就是
max
i
=
0
,
⋯
,
n
−
1
;
j
=
0
,
⋯
,
m
−
1
d
p
[
i
]
[
j
]
max_{i=0,cdots,n-1;j=0,cdots,m-1}dp[i][j]
i=0,⋯,n−1;j=0,⋯,m−1maxdp[i][j]
现在我们来讨论一下
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j]怎么求
- 如果matrix[i][j]=‘0’,很显然,dp[i][j]=0
- 如果matrix[i][j]=‘1’,那么,我们考虑三个dp: d p [ i + 1 ] [ j ] dp[i+1][j] dp[i+1][j], d p [ i + 1 ] [ j + 1 ] dp[i+1][j+1] dp[i+1][j+1], d p [ i ] [ j + 1 ] dp[i][j+1] dp[i][j+1]
我们来证明: d p [ i ] [ j ] = 1 + min ( d p [ i + 1 ] [ j ] , d p [ i + 1 ] [ j + 1 ] , d p [ i ] [ j + 1 ] ) dp[i][j]=1+min(dp[i+1][j],dp[i+1][j+1],dp[i][j+1]) dp[i][j]=1+min(dp[i+1][j],dp[i+1][j+1],dp[i][j+1])
我们证明 d p [ i ] [ j ] ≤ 1 + d p [ i + 1 ] [ j ] dp[i][j]leq 1+dp[i+1][j] dp[i][j]≤1+dp[i+1][j]
如果
d
p
[
i
]
[
j
]
>
1
+
d
p
[
i
+
1
]
[
j
]
dp[i][j]>1+dp[i+1][j]
dp[i][j]>1+dp[i+1][j],那么以
(
i
,
j
)
(i,j)
(i,j)为左上顶点,边长为
2
+
d
p
[
i
+
1
]
[
j
]
2+dp[i+1][j]
2+dp[i+1][j]的区域都是’1’,宽的范围是
[
i
,
i
+
1
+
d
p
[
i
+
1
]
[
j
]
]
[i,i+1+dp[i+1][j]]
[i,i+1+dp[i+1][j]],长的范围是
[
j
,
j
+
1
+
d
p
[
i
+
1
]
[
j
]
]
[j,j+1+dp[i+1][j]]
[j,j+1+dp[i+1][j]],这个范围(下图最大的正方形区域)内都’1’,于是,
[
i
+
1
,
i
+
1
+
d
p
[
i
+
1
]
[
j
]
]
×
[
j
,
j
+
d
p
[
i
+
1
]
[
j
]
]
[i+1,i+1+dp[i+1][j]]times[j,j+dp[i+1][j]]
[i+1,i+1+dp[i+1][j]]×[j,j+dp[i+1][j]]
这个正方形区域都是’1’。左顶点是
(
i
+
1
,
j
)
(i+1,j)
(i+1,j),边长是
d
p
[
i
+
1
]
[
j
]
+
1
dp[i+1][j]+1
dp[i+1][j]+1(下图红色的正方形区域),与
d
p
[
i
+
1
]
[
j
]
dp[i+1][j]
dp[i+1][j]的定义(下图绿色的正方形区域)矛盾。
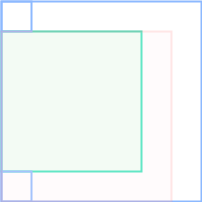
同样的方式,我们可以得到 d p [ i ] [ j ] ≤ 1 + d p [ i ] [ j + 1 ] , d p [ i ] [ j ] ≤ 1 + d p [ i + 1 ] [ j + 1 ] dp[i][j]leq 1+dp[i][j+1],dp[i][j]leq 1+dp[i+1][j+1] dp[i][j]≤1+dp[i][j+1],dp[i][j]≤1+dp[i+1][j+1]
所以, d p [ i ] [ j ] ≤ 1 + min ( d p [ i + 1 ] [ j ] , d p [ i + 1 ] [ j + 1 ] , d p [ i ] [ j + 1 ] ) dp[i][j]leq 1+min(dp[i+1][j],dp[i+1][j+1],dp[i][j+1]) dp[i][j]≤1+min(dp[i+1][j],dp[i+1][j+1],dp[i][j+1])
设 k = min ( d p [ i + 1 ] [ j ] , d p [ i + 1 ] [ j + 1 ] , d p [ i ] [ j + 1 ] ) k=min(dp[i+1][j],dp[i+1][j+1],dp[i][j+1]) k=min(dp[i+1][j],dp[i+1][j+1],dp[i][j+1]),我们证明:以 ( i , j ) (i,j) (i,j)为顶点,边长为 1 + k 1+k 1+k的正方形区域都是’1’,这个正方形区域是 [ i , i + k ] × [ j , j + k ] [i,i+k]times[j,j+k] [i,i+k]×[j,j+k]。
由
d
p
[
i
+
1
]
[
j
]
,
d
p
[
i
+
1
]
[
j
+
1
]
,
d
p
[
i
]
[
j
+
1
]
dp[i+1][j],dp[i+1][j+1],dp[i][j+1]
dp[i+1][j],dp[i+1][j+1],dp[i][j+1]的定义,三个正方形区域
A
1
=
[
i
+
1
,
i
+
k
]
×
[
j
,
j
+
k
−
1
]
A
2
=
[
i
+
1
,
i
+
k
]
×
[
j
+
1
,
j
+
k
]
A
3
=
[
i
,
i
+
k
−
1
]
×
[
j
+
1
,
j
+
k
]
begin{aligned} A_1=[i+1,i+k]times[j,j+k-1]\\ A_2=[i+1,i+k]times[j+1,j+k]\\ A_3=[i,i+k-1]times[j+1,j+k] end{aligned}
A1=[i+1,i+k]×[j,j+k−1]A2=[i+1,i+k]×[j+1,j+k]A3=[i,i+k−1]×[j+1,j+k]都是’1’,这三个区域的并为
[
i
,
i
+
k
]
×
[
j
,
j
+
k
]
[i,i+k]times[j,j+k]
[i,i+k]×[j,j+k]去掉左上方的网格,而matrix[i][j]=‘1’,所以正方形区域
[
i
,
i
+
k
]
×
[
j
,
j
+
k
]
[i,i+k]times[j,j+k]
[i,i+k]×[j,j+k]全是’1’,因此
d
p
[
i
]
[
j
]
≥
1
+
k
dp[i][j]geq 1+k
dp[i][j]≥1+k
所以
d
p
[
i
]
[
j
]
=
1
+
k
=
1
+
min
(
d
p
[
i
+
1
]
[
j
]
,
d
p
[
i
+
1
]
[
j
+
1
]
,
d
p
[
i
]
[
j
+
1
]
)
dp[i][j]=1+k=1+min(dp[i+1][j],dp[i+1][j+1],dp[i][j+1])
dp[i][j]=1+k=1+min(dp[i+1][j],dp[i+1][j+1],dp[i][j+1])这就是这个问题的状态转移方程,C++代码如下:
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int n = matrix.size();
int m = matrix[0].size();
vector<int> dp(m,0);
//最后一行初始化
int maxLen = 0;
for(int i=0;i<m;i++){
dp[i]=(matrix[n-1][i]=='1')?1:0;
maxLen=max(maxLen,dp[i]);
}
//动态规划
for(int i=n-2;i>=0;i--){
int tmp2=dp[m-1];
dp[m-1]=(matrix[i][m-1]=='1')?1:0;
maxLen=(maxLen>dp[m-1])?maxLen:dp[m-1];
for(int j=m-2;j>=0;j--){
int tmp1=dp[j];
if(matrix[i][j]=='0') {
dp[j]=0;
tmp2=tmp1;
continue;
}
else{
dp[j]=1+min(tmp1,min(tmp2,dp[j+1]));
maxLen=max(maxLen,dp[j]);
tmp2=tmp1;
}
}
}
return maxLen*maxLen;
}
};
矩阵中最长递增路径
从上面几道题目我们可以看出:矩阵上的动态规划问题的状态一般定义成在矩阵中的位置,按一定顺序求出dp矩阵即可,然而某些时候dp矩阵的求解顺序并不好确定,这个时候需要用到记忆化搜索的技巧,下面这道题目就是不好确定求解顺序的一道题目。
矩阵中最长递增路径
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
我们很容易想到将 d p [ i ] [ j ] dp[i][j] dp[i][j]定义成以 ( i , j ) (i,j) (i,j)为头的最长递增序列,再取最大值,状态转移方程就是接上四个方向的最长递增序列,由于四个方向都可以延续,所以不知道从哪个位置开始计算,这个时候可以用记忆化搜索的技巧,代码如下:
class Solution {
private:
vector<vector<int>> dp;
int n,m,maxLen;
void longestIncreasingPath(vector<vector<int>>& matrix,int i,int j){
dp[i][j]=1;
//上
if(i>0&&matrix[i-1][j]>matrix[i][j]){
if(dp[i-1][j]<0) longestIncreasingPath(matrix,i-1,j);
dp[i][j]+=dp[i-1][j];
}
//下
if(i<n-1&&matrix[i+1][j]>matrix[i][j]){
if(dp[i+1][j]<0) longestIncreasingPath(matrix, i+1, j);
dp[i][j]=max(dp[i][j],1+dp[i+1][j]);
}
//左
if(j>0&&matrix[i][j-1]>matrix[i][j]){
if(dp[i][j-1]<0) longestIncreasingPath(matrix,i,j-1);
dp[i][j]=max(dp[i][j],dp[i][j-1]+1);
}
//右
if(j<m-1&&matrix[i][j+1]>matrix[i][j]){
if(dp[i][j+1]<0) longestIncreasingPath(matrix,i,j+1);
dp[i][j]=max(dp[i][j],dp[i][j+1]);
}
maxLen=max(maxLen,dp[i][j]);
}
public:
int longestIncreasingPath(vector<vector<int>>& matrix) {
n=matrix.size();
m=matrix[0].size();
if(n==1){
int lag=1;
bool asc;
int maxlag=1;
for(int j=1;j<m;j++){
if(lag==1){
if(matrix[0][j]!=matrix[0][j-1]){
lag++;
asc=(matrix[0][j]>matrix[0][j-1]);
}
}else if(matrix[0][j]==matrix[0][j-1]){
maxlag=max(maxlag,lag);
lag=1;
}else if(asc){
if(matrix[0][j]>matrix[0][j-1]) lag++;
else{
maxlag=max(maxlag,lag);
lag=2;
asc=false;
}
}else{
if(matrix[0][j]<matrix[0][j-1]) lag++;
else{
maxlag=max(maxlag,lag);
lag=2;
asc=true;
}
}
}
return maxlag;
}else if(m==1){
int lag=1;
bool asc;
int maxlag=1;
for(int i=1;i<n;i++){
if(lag==1){
if(matrix[i][0]!=matrix[i-1][0]){
lag++;
asc=(matrix[i][0]>matrix[i-1][0]);
}
}else if(matrix[i][0]==matrix[i-1][0]){
maxlag=max(maxlag,lag);
lag=1;
}else if(asc){
if(matrix[i][0]>matrix[i-1][0]) lag++;
else{
maxlag=max(maxlag,lag);
lag=2;
asc=false;
}
}else{
if(matrix[i][0]<matrix[i-1][0]) lag++;
else{
maxlag=max(maxlag,lag);
lag=2;
asc=true;
}
}
}
return maxlag;
}else{
dp=vector<vector<int>>(n,vector<int>(m,-1));
maxLen=1;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(dp[i][j]<0) longestIncreasingPath(matrix, i, j);
}
}
return maxLen;
}
}
};
最后
以上就是威武书包最近收集整理的关于动态规划7:矩阵上的动态规划的全部内容,更多相关动态规划7:矩阵上内容请搜索靠谱客的其他文章。









发表评论 取消回复