hdu 2604 Queuing （矩阵快速幂）分析代码

62 阅读 0 评论 41 点赞

我是靠谱客的博主幽默毛豆，最近开发中收集的这篇文章主要介绍hdu 2604 Queuing （矩阵快速幂）分析代码，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Queuing

分析

一般递推式
向量递推式
状态机模型 1

以最后3个人的性别序列为状态标识
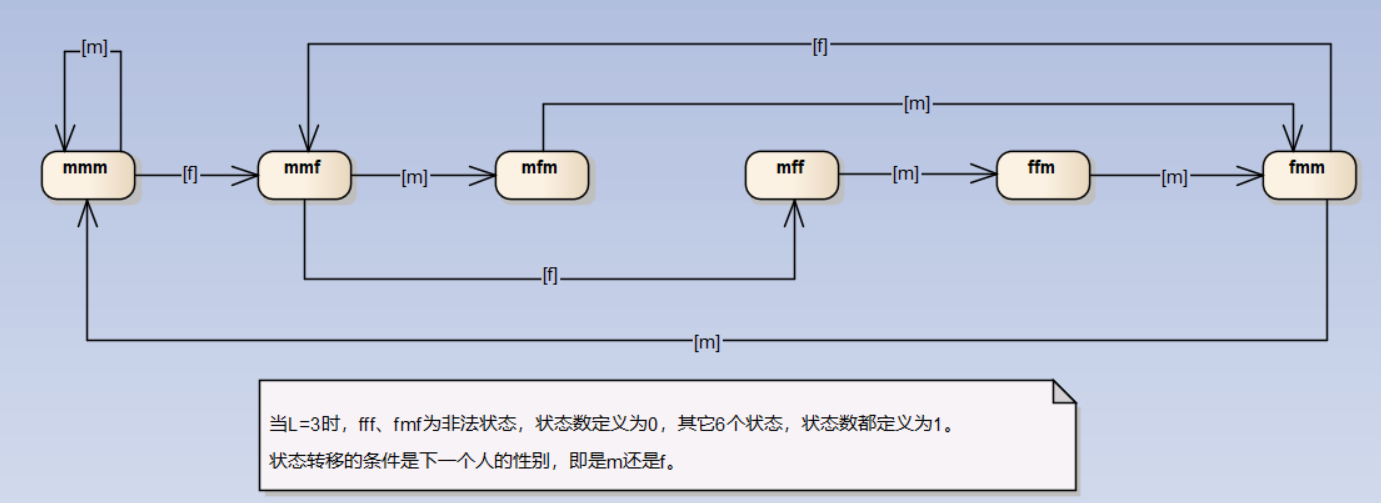
在这里插入图片描述
转移方程：
S_mmm = S_mmm + S_fmm // S₀ = S₀ + S₄
S_mmf = S_mmm + S_fmm // S₁ = S₀ + S₄
S_mfm = S_mmf // S₂ = S₁
S_mff = S_mmf // S₃ = S₁
S_fmm= S_mfm + S_ffm // S₄= S₂ + S₆
S_fmf= 0 // S₅ = 0
S_ffm = S_mff // S₆ = S₃
S_fff = 0 // S₇ = 0
转移矩阵
在这里插入图片描述

状态机模型 2

转移方程：
S₀ = S₀ + S₃
S₁ = S₀
S₂ = S₁
S₃ = S₁ + S₂
初始状态
当L=1时，S₀ = 1、S₁ = 1、 S₂ = 0、S₃ = 0
转移矩阵

代码

一般递推式

超时（TLE），不可行

#include<bits/stdc++.h>
using namespace std;
#define MXN 1000010
#define mod(x) ((x)%M)
int L, M, dp[MXN]={0, 2, 4, 6, 9};
int main(){
    while(scanf("%d%d", &L, &M) == 2){
        for(int i = 5; i <= MXN; i++)
            dp[i] = mod(dp[i-1]+dp[i-3]+dp[i-4]);        
        printf("%dn", dp[L]%M);
    }
    return 0;
}

勉强过关【耗时：4165MS】

#include<bits/stdc++.h>
using namespace std;
#define MXN 1000010
#define mod(x) ((x)%M)
int L, M, dp[MXN]={0, 2, 4, 6, 9};
int main(){
    while(scanf("%d%d", &L, &M) == 2){
        for(int i = 5; i <= L; i++){
            dp[i] = dp[i-1]+dp[i-3]+dp[i-4];
            if(dp[i] > 1000000) dp[i] %= M;
        }      
        printf("%dn", dp[L]%M);
    }
    return 0;
}

向量递推式【耗时：93ms】

#include<bits/stdc++.h>
using namespace std;
#define MXM 4
#define mod(x) ((x)%M)
int L, M, f[5]={0, 2, 4, 6, 9}, A[MXM][MXM]={{1,0,1,1},{1,0,0,0},{0,1,0,0},{0,0,1,0}};
struct mat{ 
    int d[MXM][MXM];
    mat operator*(const mat x){
        mat ret;
        int tmp;
        for(int i = 0; i < MXM; i++){
            for(int j = 0; j < MXM; j++){
                tmp = 0;
                for(int k = 0; k < MXM; k++){
                    tmp = mod(tmp + d[i][k]* x.d[k][j]);
                }
                ret.d[i][j] = tmp;
            }
        }
        return ret;
    }
    void init_unit(){
        for(int i = 0; i < MXM; i++)
            for(int j = 0; j < MXM; j++)
                d[i][j] = i == j ? 1 : 0;
    }
    void init(){
        for(int i = 0; i < MXM; i++){
            for(int j = 0; j < MXM; j++){
                this->d[i][j] = A[i][j];
            }
        }
    }
}ma;
mat matrixPow(mat base, int pow){
    mat res;
    res.init_unit();
    while(pow){
        if(pow & 1) res = res * base;
        base = base * base;
        pow >>= 1;
    }
    return res;
}
int main(){
    while(scanf("%d%d", &L, &M) == 2){
        if(L <= MXM){
			printf("%dn", f[L]%M);
			continue;
		}
        ma.init();
        ma = matrixPow(ma, L-4);
        int ans = 0;
        for(int i = 0; i < MXM; i++)
            ans = mod(ans+ma.d[0][i]*f[MXM-i]);
        printf("%dn", ans);
    }
	return 0;
}

状态转移 1 【耗时：2636ms】

#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define MXM 8
#define mod(x) ((x)%M)
int L, M, s[3]={0,2,4}, f[8]={1,1,1,1,1,0,1,0};
int A[MXM][MXM]={{1,0,0,0,1,0,0,0},{1,0,0,0,1,0,0,0},
    {0,1,0,0,0,0,0,0},{0,1,0,0,0,0,0,0},
    {0,0,1,0,0,0,1,0},{0,0,0,0,0,0,0,0},
    {0,0,0,1,0,0,0,0},{0,0,0,0,0,0,0,0}};
struct mat{ 
    LL d[MXM][MXM];
    mat operator*(const mat x){
        mat ret;
        LL tmp;
        for(int i = 0; i < MXM; i++){
            for(int j = 0; j < MXM; j++){
                tmp = 0;
                for(int k = 0; k < MXM; k++){
                    tmp = mod(tmp + d[i][k]* x.d[k][j]);
                }
                ret.d[i][j] = tmp;
            }
        }
        return ret;
    }
    void init_unit(){ // 初始化为单位矩阵
        for(int i = 0; i < MXM; i++)
            for(int j = 0; j < MXM; j++)
                d[i][j] = i == j ? 1 : 0;
    }
    void init(){ // 初始化为变换矩阵
        for(int i = 0; i < MXM; i++)
            for(int j = 0; j < MXM; j++)
                this->d[i][j] = A[i][j];          
    }
}ma;
mat matrixPow(mat base, LL pow){
    mat res;
    res.init_unit();
    while(pow){
        if(pow & 1) res = res * base;
        base = base * base;
        pow >>= 1;
    }
    return res;
}
int main(){
	while(scanf("%d%d", &L, &M) == 2){
        if(L <= 2){
			printf("%dn", s[L]%M);
			continue;
		}
        ma.init();
        ma = matrixPow(ma, L-3);
        int ans = 0;
        for(int i = 0; i < MXM; i++)
            for(int j = 0; j < MXM; j++)
                ans = mod(ans+ma.d[i][j]*f[j]);
        printf("%dn", ans);
    }
	return 0;
}

状态转移 2 【耗时：93MS】

#include<bits/stdc++.h>
using namespace std;
#define MXM 4
#define mod(x) ((x)%M)
int L, M, A[MXM][MXM]={{1,0,0,1},{1,0,0,0},{0,1,0,0},{0,1,1,0}};
struct mat{ 
    int d[MXM][MXM];
    mat operator*(const mat x){
        mat ret;
        int tmp;
        for(int i = 0; i < MXM; i++){
            for(int j = 0; j < MXM; j++){
                tmp = 0;
                for(int k = 0; k < MXM; k++){
                    tmp = mod(tmp + d[i][k]* x.d[k][j]);
                }
                ret.d[i][j] = tmp;
            }
        }
        return ret;
    }
    void init_unit(){
        for(int i = 0; i < MXM; i++)
            for(int j = 0; j < MXM; j++)
                d[i][j] = i == j ? 1 : 0;
    }
    void init(){
        for(int i = 0; i < MXM; i++){
            for(int j = 0; j < MXM; j++){
                this->d[i][j] = A[i][j];
            }
        }
    }
}ma;
mat matrixPow(mat base, int pow){
    mat res;
    res.init_unit();
    while(pow){
        if(pow & 1) res = res * base;
        base = base * base;
        pow >>= 1;
    }
    return res;
}
int main(){
    while(scanf("%d%d", &L, &M) == 2){
        if(L == 0){ printf("0n"); continue;}
        ma.init();
        ma = matrixPow(ma, L-1);
        int ans = 0;
        for(int i = 0; i < MXM; i++)
            ans = mod(ans+ma.d[i][0]+ma.d[i][1]);
        printf("%dn", ans);
    }
	return 0;
}