【LeetCode】只出现一次的数字系列

68 阅读 0 评论 45 点赞

我是靠谱客的博主紧张薯片，最近开发中收集的这篇文章主要介绍【LeetCode】只出现一次的数字系列，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1、136. 只出现一次的数字
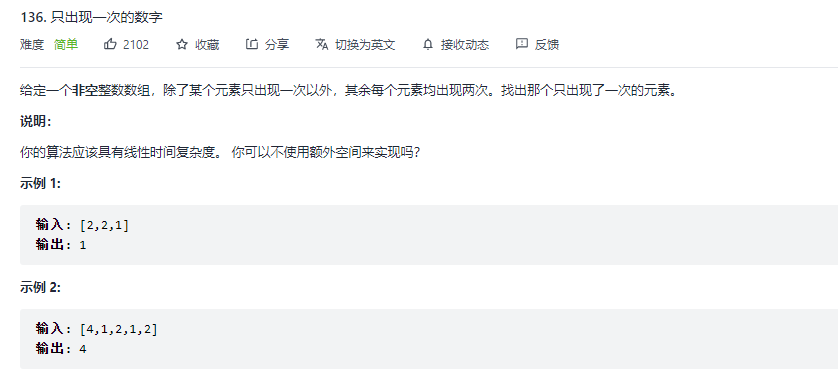
在这里插入图片描述
思路很简单，这道题很特殊，因为只有一个数出现了一次，其余的出现了两次，我们知道异或运算对于相同的数字异或结果都为0，因此采用异或运算能很快解决这个题目。

class Solution {
    public int singleNumber(int[] nums) {
        int ans=0;
        for(int num:nums){
            ans^=num;
        }
        return ans;
    }
}

2、137. 只出现一次的数字 II

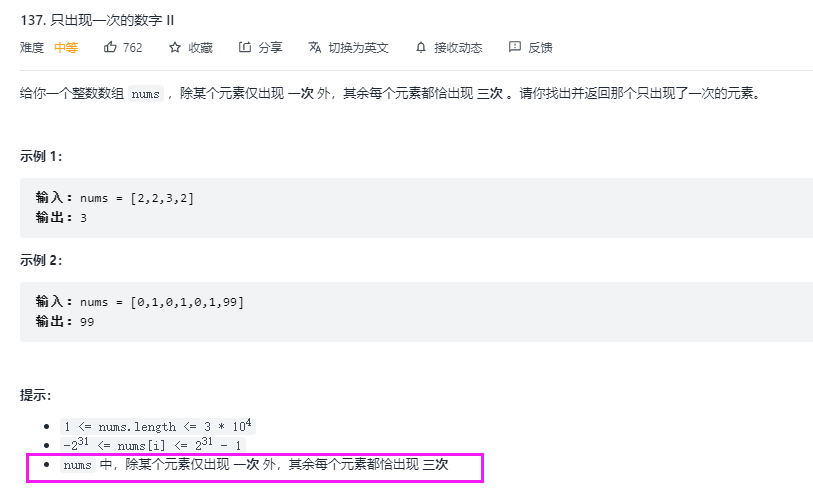
在这里插入图片描述
思路：采用复杂度稍微高点的思路，不过比较好理解。数据范围为int，因此对每一个二进制位进行检查，如果这个二进制位上为1的数不能整除3，那么只出现一次的数该位置上必为1，记录在答案上即可。
代码：

class Solution {
    public int singleNumber(int[] nums) {
        int res=0;
        for(int i=1;i<=32;i++){
            int sum=0;
            for(int num:nums){
                int tem=num>>i&1;
                if(tem>0) sum++;
            }
            if(sum%3!=0){
                res|=1<<i;
            }
        }
        return res;
    }
}

3、进阶版：260. 只出现一次的数字 III
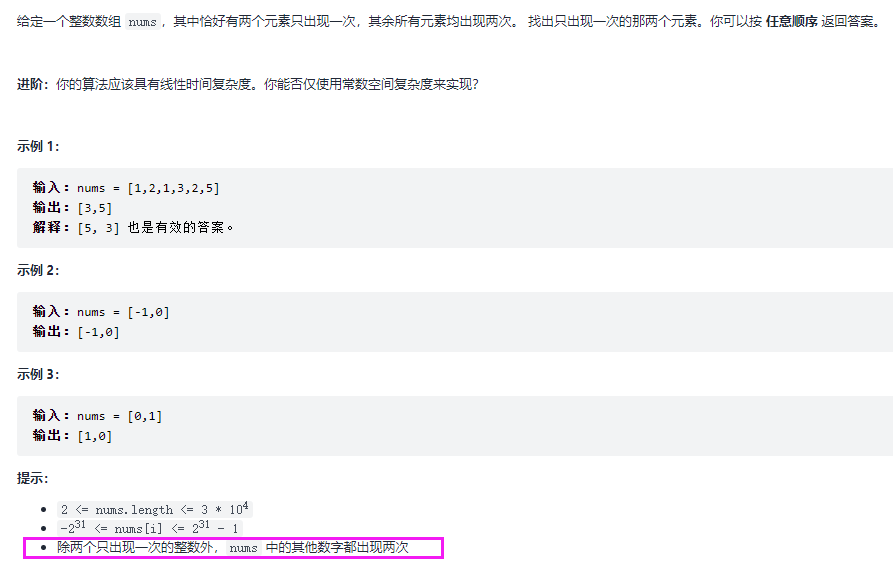
在这里插入图片描述
思路：有了上面的经验，我们同样先对所有数都异或一遍得到一个结果，这个结果刚好为这两个只出现一次的数的异或结果，因此，我们需要利用这个结果反过来得到这两个数。首先，我们知道两个数异或，那么结果为1的位，必然是一个为1一个为0，根据这一特性，我们就可以将所有的数进行分组，根据抑或结果中二进制位为1的位对数组中的数进行分组，假设我们取最低位为1的位置，此时分为这样的两组，第一组数在这个位上的二进制都为1，另一组都为0，此时将两组分别进行异或即可得到结果了。

那么问题来了，为什么要取最低有效位？ 因为它是我们对两个数字划分的一种方式，当两个数字的异或某位值为1时，必然存在两个数字在此位上的值不相同。我们取最低有效位，其实是一种划分，其实取任意一位都可以，因为位运算中，取最低位的1比较方便，所以可选的情况下通常选取最低位。

代码：

class Solution {
    public int[] singleNumber(int[] nums) {
        int ans=0;
        for(int num:nums) ans^=num;
        int res[]=new int[2];
        res[0]=res[1]=0;
        int index=getIndex(ans); //找出第一个二进制位为1的位置，以这个来进行分组
        for(int num:nums){
            if(((num>>index)&1)==0){
                res[0]^=num;
            }else{
                res[1]^=num;
            }
        }
        return res;
    }
    
    public int getIndex(int num){
        int index=0;
        while(index<32&&((num&1)==0)){
            index++;
            num>>=1;
        }
        return index;
    }
}

代码2：

class Solution {
    public int[] singleNumber(int[] nums) {
        int ans=0;
        for(int num:nums) ans^=num;
        int res[]=new int[2];
        res[0]=res[1]=0;
        // 一个数&本身相反数得到二进制位为1的最低位，利用反码运算的，别搞混了
        int index=(ans==Integer.MIN_VALUE?ans:ans&(-ans)); //防止溢出
        for(int num:nums){
            if((num&index)>0){
                res[0]^=num;
            }else{
                res[1]^=num;
            }
        }
        return res;
    }
}

扩展，我们再来看牛客网上这道题：NC156 数组中只出现一次的数（其它数出现k次）
这题是不是直接利用int范围的二进制位进行统计就可以得出结果了，对于出现k次，进行分情况讨论，如果k为偶数，那最终异或结果必然为0，如果为奇数，那么我们再看每个二进制位上是否满足模k等于0，如果不等于，则这个只出现一次的数字在这个二进制位上必然为1，记录在答案中即可。
代码·：

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param arr int一维数组 
     * @param k int 
     * @return int
     */
    public int foundOnceNumber (int[] arr, int k) {
        int ans=0;
        for(int num: arr){
            ans^=num;
        }
        if(k%2==0) return ans;
        ans=0;
        for(int i=0;i<32;i++){ //枚举32位二进制位
            int temp=0;
            for(int num:arr){
                temp+=(num>>>i)&1; //依次右移num，同1相与，计算每一位上1的个数
            }
            if(temp%k!=0){ //必然这个数在该二进制位上为1,记录在答案中
                ans|=1<<i;
            }
        }
        return ans;
    }
}