文章目录
- 一、查找(搜索)基础
- 1.顺序查找
- 2.二分查找
- 3.插值查找
- 4.斐波那契查找
- 5.线性索引查找
- 5.1 稠密索引
- 5.2 分块索引
- 5.3 倒排索引
- 二、二分查找leetcode总结
一、查找(搜索)基础
我们常用的搜索引擎的原理如下:
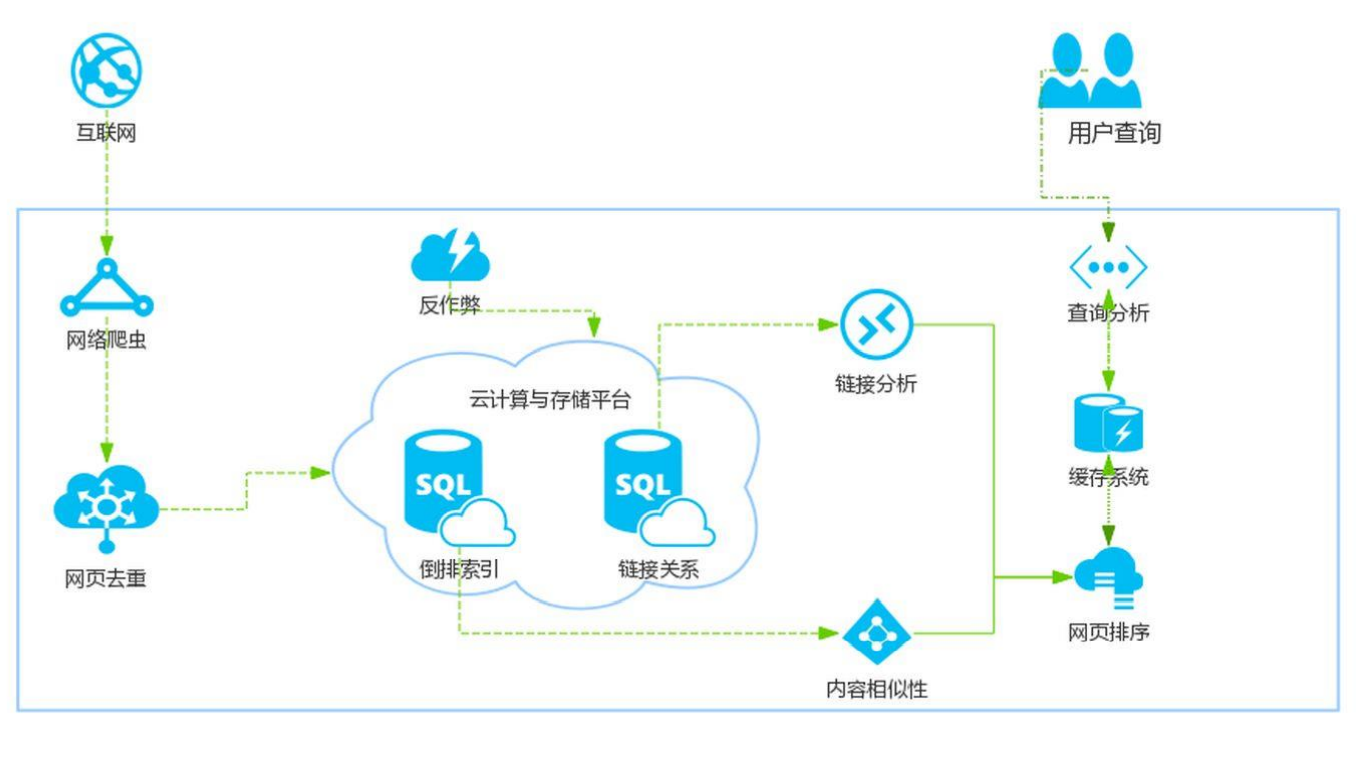
下面介绍一些概念:
- 查找(Searching)
就是根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素(或记录)。 - 查找表(Search Table)
由同一类型的数据元素((或记录)构成的集合 - 关键字(Key)
数据元素中某个数据项的值,又称为键值。 - 主键(Primary Key)
可唯一地标识某个数据元素或记录的关键字。
查找表按照操作方式可分为:
- 静态查找表(Static Search Table):只做查找操作的查找表。
它的主要操作是:查询某个“特定的”数据元素是否在表中、检索某个“特定的”数据元素和各种属性 - 动态查找表(Dynamic Search Table):在查找中同时进行插入或删除等操作
查找时插入数据、查找时删除数据
1.顺序查找
顺序查找也称为线性查找,属于无序查找算法,顺序查找适合于存储结构为顺序存储或链接存储的线性表。其基本思想是:从数据结构线形表的一端开始,顺序扫描,依次将扫描到的结点关键字与给定值k相比较,若相等则表示查找成功;若扫描结束仍没有找到关键字等于k的结点,表示查找失败。
时间复杂度分析:查找成功时的平均查找长度为 n + 1 2 frac{n+1}2 2n+1
查找失败时,查找长度为 n n n
所以顺序查找的时间复杂度为 O ( n ) O(n) O(n)
# 最基础的遍历无序列表的查找算法,时间复杂度为O(n)
def sequential_search(lis, key):
length = len(lis)
for i in range(length):
if lis[i] == key:
return i
else:
return False
if __name__ == '__main__':
nums = [1, 2, 3, 4, 5, 6, 7, 8]
target = 6
result = sequential_search(nums, target)
print(result)
def sequential_search(lis, key):
i = 0
# 往列表末尾防止哨兵,省去了遍历时判断查找是否越界的过程,数据量大时,效果显著
lis.append(key)
while lis[i] != key:
i += 1
# 如果i等于列表长度(最后一个元素索引+1),说明查找失败,否则查找成功
return i
if __name__ == '__main__':
nums = [1, 2, 3, 4, 5, 6, 7, 8]
target = 6
result = sequential_search(nums, target)
print(result)
2.二分查找
二分查找也称折半查找(Binary Search),是一种在有序数组中查找某一特定元素的搜索算法。我们可以从定义可知,运用二分搜索的前提是数组必须是有序的,这里需要注意的是,我们的输入不一定是数组,也可以是数组中某一区间的起始位置和终止位置。
二分查找要注重代码细节,容易出错
二分查找的执行过程如下:
- 从已经排好序的数组或区间中,取出中间位置的元素,将其与我们的目标值进行比较,判断是否相等,如果相等则返回。
- 如果
nums[mid]和target不相等,则对nums[mid]和target值进行比较大小,通过比较结果决定是从mid的左半部分还是右半部分继续搜索。
如果target > nums[mid]则右半区间继续进行搜索,即left = mid + 1;
若target < nums[mid]则在左半区间继续进行搜索,即right = mid -1
二分查找过程举例:target = 8
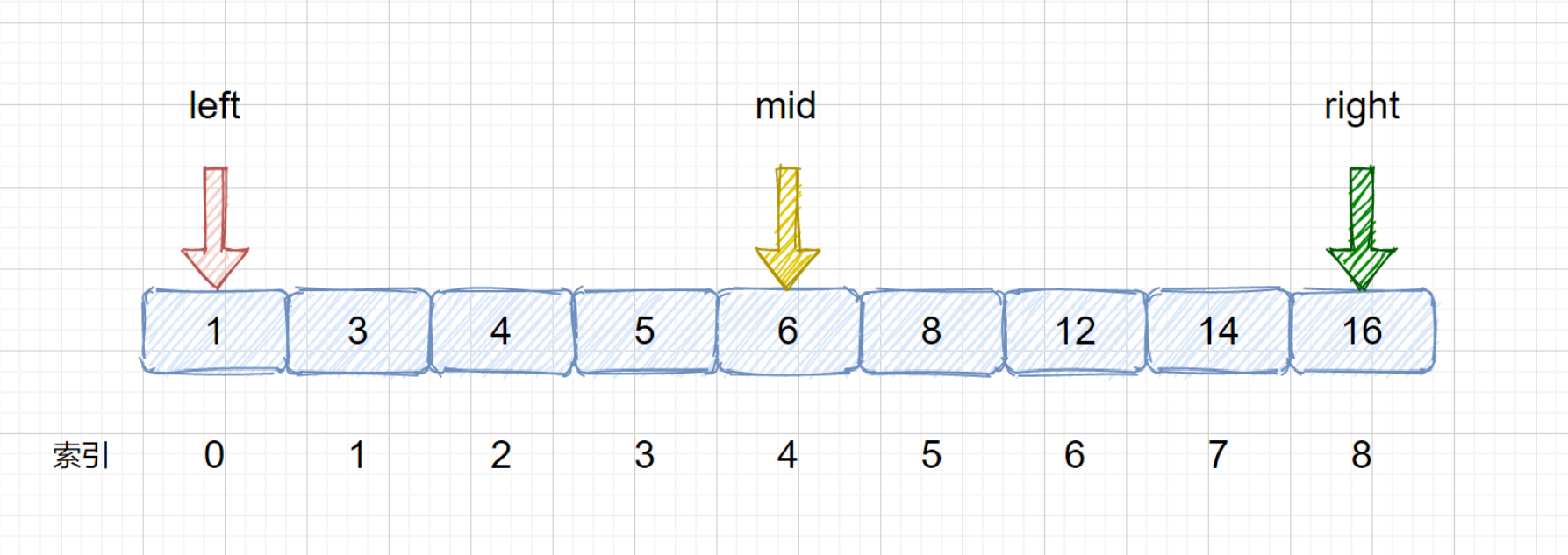
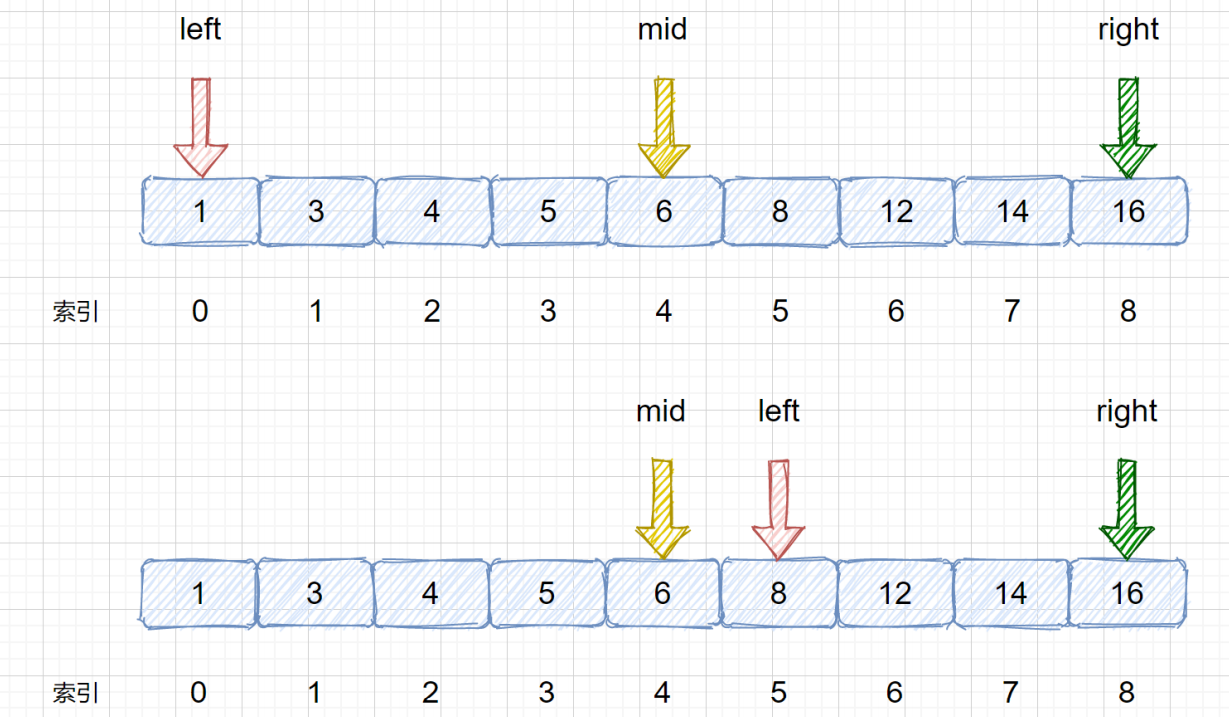
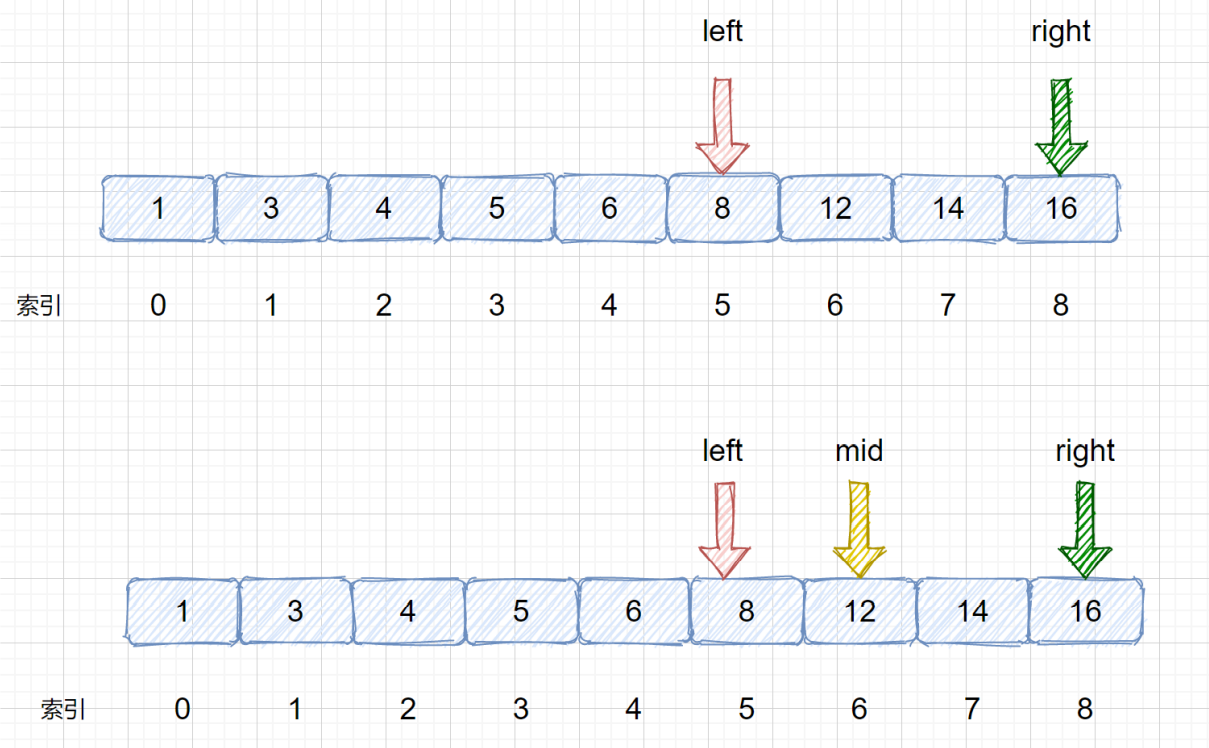
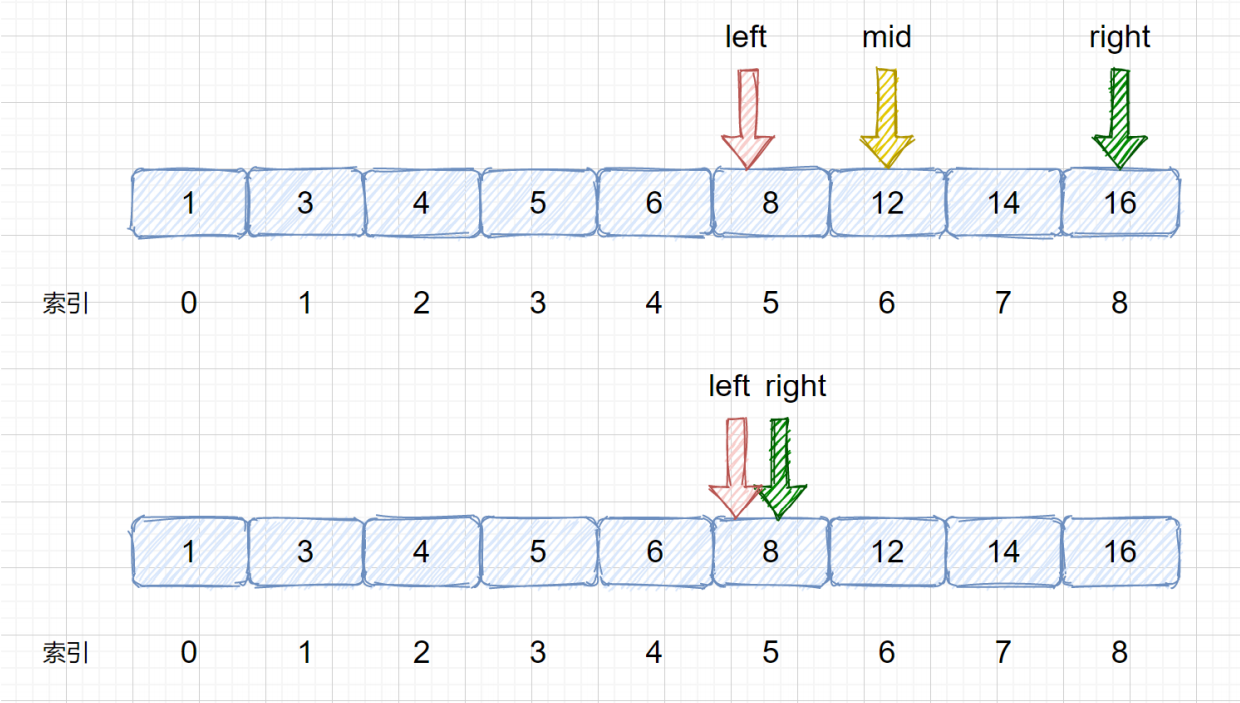
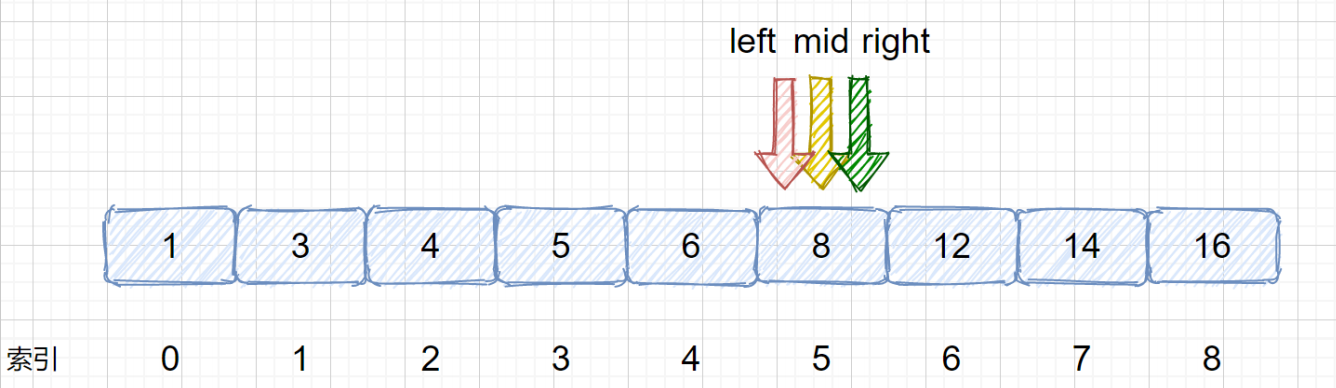
# 针对有序查找表的二分查找算法
# 时间复杂度为O(log(n))
def binary_serach(lis, key):
low = 0
high = len(lis) - 1
# 这里如果low<high,mid会移到12后,low = high = 8,此时跳出循环,返回False
while low <= high:
mid = int(low + (high - low) / 2)
if lis[mid] == key:
return mid
elif lis[mid] > key:
high = mid - 1
elif lis[mid] < key:
low = mid + 1
# 循环结束时,low > high,上面的mid-1,smid+1是为了避免出现死循环
return False
if __name__ == '__main__':
nums = [1, 3, 4, 5, 6, 8, 12, 14, 16]
target = 8
result = binary_serach(nums, target)
print(result)
时间复杂度分析:
由二叉树的性质:具有n个结点的完全二叉树的深度必为
[
l
o
g
2
n
]
+
1
[log_2n]+1
[log2n]+1
[x]表示不大于x的最大整数
我们知道最坏时间复杂度为 O ( l o g 2 n ) O(log_2{n}) O(log2n)
3.插值查找
二分查找法相对于顺序查找法虽然已经很不错了,但还有可以优化的地方。有的时候,对半过滤还不够狠,要是每次都排除十分之九的数据岂不是更好?选择这个值就是关键问题。插值的意义就是:以更快的速度进行缩减。插值的核心就是使用公式:
v
a
l
u
e
=
k
e
y
−
l
i
s
t
[
l
o
w
]
l
i
s
t
[
h
i
g
h
]
−
l
i
s
t
[
l
o
w
]
value = frac{key - list[low]}{list[high] - list[low]}
value=list[high]−list[low]key−list[low]
用着
v
a
l
u
e
value
value来代替二分查找中的
1
2
frac12
21。
m
i
d
=
l
o
w
+
k
e
y
−
l
i
s
t
[
l
o
w
]
l
i
s
t
[
h
i
g
h
]
−
l
i
s
t
[
l
o
w
]
(
h
i
g
h
−
l
o
w
)
mid=low+frac{key - list[low]}{list[high] - list[low]}(high-low)
mid=low+list[high]−list[low]key−list[low](high−low)
def interpolation_serach(lis, key):
low = 0
high = len(lis) - 1
while low <= high:
mid = int(low + ((high - low) * (key - lis[low]) / (lis[high] - lis[low])))
if lis[mid] == key:
return mid
elif lis[mid] > key:
high = mid - 1
elif lis[mid] < key:
low = mid + 1
# 循环结束时,low > high
return False
if __name__ == '__main__':
nums = [1, 3, 4, 5, 6, 8, 12, 14, 16]
target = 8
result = interpolation_serach(nums, target)
print(result)
时间复杂度分析:时间复杂度为 O ( l o g n ) O(log_n) O(logn),但是对于表长比较大,关键字分布比较均匀的查找表来说,插值查找算法的平均性能要比折半查找算法的平均性能要好很多。
4.斐波那契查找
由插值算法带来的启发,发明了斐波那契算法。其核心是:如何优化那个缩减速率,使得查找次数尽量降低。使用这种算法,前提是:已经有一个包含斐波那契数据的列表。
- 需要一个现成的斐波那契列表,其最大元素的值必须超过查找表中元素个数的数值。
- 为了使查找表满足斐波那契特性,在表的末尾添加几个原查找表的最后那个元素的值,使得查找表的长度达到步骤1的最大元素的值。
key < lis[mid]时,high = mid - 1,此时,元素个数为F[k-1] - 1
key > lis[mid]时,low = mid + 1,此时,元素个数为F[k-2] - 1
元素个数划分规律为:F[k] - 1 = F[k-1] - 1 + F[k-2] - 1 + 1(mid位置)
def fibonacci_search(lis, key):
F = [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987]
low = 0
high = len(lis) - 1
# F[k-1] < high < F[k]
k = 0
while high > F[k] - 1:
k += 1
# 循环结束的条件是high <= F[k] -1,即F[k] > high时的索引
print(k)
# 为了使查找表满足斐波那契特性,在表的末尾添加几个原查找表的最后那个元素的值
# 添加的个数由F[k] - 1 - high决定
i = high
while F[k] - 1 > i:
lis.append(lis[high])
i += 1
while low <= high:
# 为了防止F列表下标溢出,设置if和else
if k < 2:
mid = low
else:
mid = low + F[k - 1] - 1
print("low=%s,mid=%s,high=%s", (low, mid, high))
if key < lis[mid]:
high = mid - 1
k -= 1
elif key > lis[mid]:
low = mid + 1
k -= 2
else:
if mid <= high:
return mid
else:
return high
return False
if __name__ == '__main__':
nums = [0, 1, 16, 24, 35, 47, 59, 62, 73, 88, 99]
target = 59
result = fibonacci_search(nums, target)
print(result)
7
low=%s,mid=%s,high=%s (0, 7, 10)
low=%s,mid=%s,high=%s (0, 4, 6)
low=%s,mid=%s,high=%s (5, 6, 6)
6
5.线性索引查找
对于海量的无序数据,为了提高查找速度,一般会为其构造索引表。索引就是把一个关键字与它相对应的记录进行关联的过程。一个索引由若干个索引项构成,每个索引项至少包含关键字和其对应的记录在存储器中的位置等信息。 索引按照结构可以分为:线性索引、树形索引和多级索引。
线性索引:将索引项的集合通过线性结构来组织,也叫索引表。
线性索引可分为:稠密索引、分块索引和倒排索引
5.1 稠密索引
稠密索引指的是在线性索引中,为数据集合中的每个记录都建立一个索引项。这其实就相当于给无序的集合,建立了一张有序的线性表。其索引项一定是按照关键码进行有序的排列。这也相当于把查找过程中需要的排序工作给提前做了。
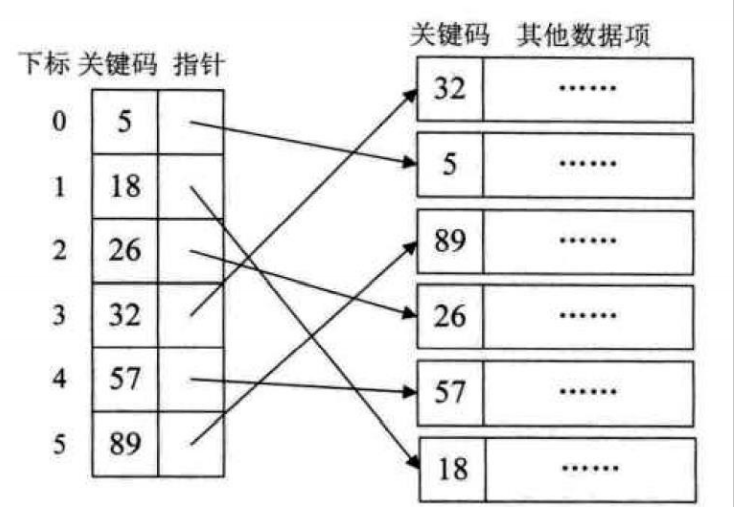
如果数据集特别大时,索引也需要同样的数据集规模,对于内存有限的计算机来说,就需要反复访问磁盘,查找性能反而下降了。稠密索引空间代价比较大
5.2 分块索引
给大量的无序数据集合进行分块处理,使得块内无序,块间有序。这其实是有序查找和无序查找的一种中间状态或者说妥协状态。因为数据量过大,建立完整的稠密索引耗时耗力,占用资源过多;但如果不做任何排序或者索引,那么遍历的查找也无法接受,只能折中,做一定程度的排序或索引。
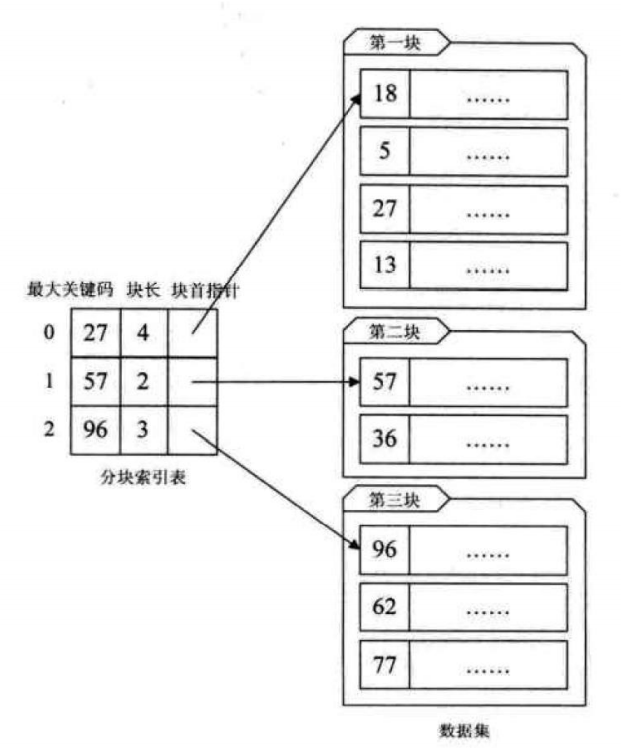
时间复杂度分析:分块索引的效率比遍历查找的O(n)要高一些,但与二分查找的O(logn)还是要差不少。
假设数据量为
n
n
n,共
m
m
m块,每块中有
t
t
t条。块查找的平均查找长度为
m
+
1
2
frac{m+1}2
2m+1,块中查找的平均查找长度为
t
+
1
2
frac{t+1}2
2t+1,所以总的时间复杂度为
(
m
+
1
)
+
(
t
+
1
)
2
=
m
+
t
2
+
1
frac{(m+1)+(t+1)}2=frac{m+t}2+1
2(m+1)+(t+1)=2m+t+1,当
m
=
t
=
n
m=t=sqrt{n}
m=t=n时,时间复杂度为
O
(
n
)
O(sqrt{n})
O(n)。
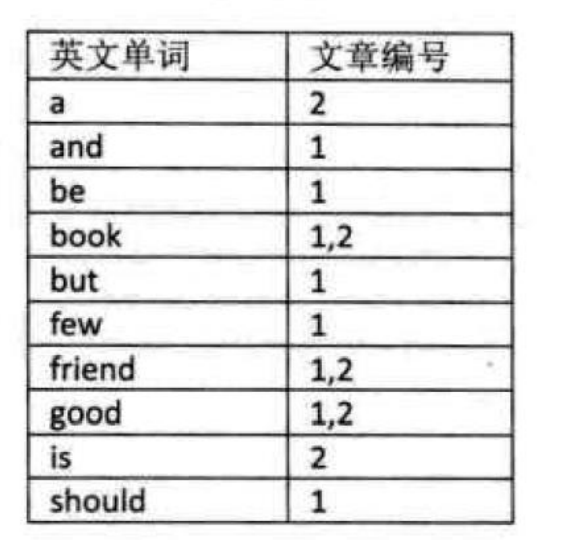
5.3 倒排索引
不是由记录来确定属性值,而是由属性值来确定记录的位置,这种被称为倒排索引。其中记录号表存储具有相同次关键字的所有记录的地址或引用(可以是指向记录的指针或该记录的主关键字)。倒排索引是最基础的搜索引擎索引技术。
二、二分查找leetcode总结
面试题 08.03. 魔术索引
35. 搜索插入位置
34. 在排序数组中查找元素的第一个和最后一个位置
33. 搜索旋转排序数组
81. 搜索旋转排序数组 II
面试题 10.03. 搜索旋转数组
153. 寻找旋转排序数组中的最小值
74. 搜索二维矩阵
240. 搜索二维矩阵 II
如果对您有帮助,麻烦点赞关注,这真的对我很重要!!!如果需要互关,请评论或者私信!

最后
以上就是高高黄蜂最近收集整理的关于数据结构与算法python—11.查找及python实现与leetcode总结的全部内容,更多相关数据结构与算法python—11内容请搜索靠谱客的其他文章。








发表评论 取消回复