位运算(Bit Operation)
- [136. 只出现一次的数字](https://leetcode-cn.com/problems/single-number/)
- [137. 只出现一次的数字 II](https://leetcode-cn.com/problems/single-number-ii/)
- [260. 只出现一次的数字 III](https://leetcode-cn.com/problems/single-number-iii/)
- [191. 位1的个数](https://leetcode-cn.com/problems/number-of-1-bits/)
- [201. 数字范围按位与](https://leetcode.cn/problems/bitwise-and-of-numbers-range/)
- [面试题 17.01. 不用加号的加法](https://leetcode.cn/problems/add-without-plus-lcci/)
- [67. 二进制求和](https://leetcode-cn.com/problems/add-binary/)
- [190. 颠倒二进制位](https://leetcode-cn.com/problems/reverse-bits/)
- 方法一:逐位颠倒
- [231. 2 的幂](https://leetcode-cn.com/problems/power-of-two/)
- [268. 丢失的数字](https://leetcode-cn.com/problems/missing-number/)
- [318. 最大单词长度乘积](https://leetcode-cn.com/problems/maximum-product-of-word-lengths/)
- 方法一:set
- 方法二:位运算
- [389. 找不同](https://leetcode-cn.com/problems/find-the-difference/)
- 方法一:计数
- 方法二:求和
- 方法三:位运算
- 方法四:列表排序
- [397. 整数替换](https://leetcode-cn.com/problems/integer-replacement/)
- 方法一:记忆化搜索
- 方法二:贪心
- [405. 数字转换为十六进制数](https://leetcode-cn.com/problems/convert-a-number-to-hexadecimal/)
- 方法一:位运算
- [458. 可怜的小猪](https://leetcode-cn.com/problems/poor-pigs/)
- [476. 数字的补数](https://leetcode-cn.com/problems/number-complement/submissions/)
- 方法一:位运算
- [剑指 Offer II 003. 前 n 个数字二进制中 1 的个数](https://leetcode.cn/problems/w3tCBm/)
- [89. 格雷编码](https://leetcode-cn.com/problems/gray-code/)
- [1611. 使整数变为 0 的最少操作次数](https://leetcode.cn/problems/minimum-one-bit-operations-to-make-integers-zero/)
- [1318. 或运算的最小翻转次数](https://leetcode.cn/problems/minimum-flips-to-make-a-or-b-equal-to-c/)
- [6169. 最长优雅子数组](https://leetcode.cn/problems/longest-nice-subarray/)
- 剑指 Offer 15. 二进制中1的个数
- 剑指 Offer 65. 不用加减乘除做加法
- 1238. 循环码排列
- 1442. 形成两个异或相等数组的三元组数目
- 1486. 数组异或操作
- 1611. 使整数变为 0 的最少操作次数
- 1655. 分配重复整数
- 1659. 最大化网格幸福感
- 1707. 与数组中元素的最大异或值
- 1723. 完成所有工作的最短时间
- 1815. 得到新鲜甜甜圈的最多组数
- 1835. 所有数对按位与结果的异或和
- 1863. 找出所有子集的异或总和再求和
- 1947. 最大兼容性评分和
- 2044. 统计按位或能得到最大值的子集数目
- 2172. 数组的最大与和
- 2220. 转换数字的最少位翻转次数
- 2275. 按位与结果大于零的最长组合
- 2317. 操作后的最大异或和
- 29. 两数相除
- 338. 比特位计数
- 393. UTF-8 编码验证
- 401. 二进制手表
- 405. 数字转换为十六进制数
- 461. 汉明距离
- 464. 我能赢吗
- 477. 汉明距离总和
- 693. 交替位二进制数
- 751. IP 到 CIDR
- 762. 二进制表示中质数个计算置位
- 810. 黑板异或游戏
- 898. 子数组按位或操作
- 982. 按位与为零的三元组
- 995. K 连续位的最小翻转次数
- [2411. 按位或最大的最小子数组长度](https://leetcode.cn/problems/smallest-subarrays-with-maximum-bitwise-or/)
- [26. 删除有序数组中的重复项](https://leetcode.cn/problems/remove-duplicates-from-sorted-array/)
- [898. 子数组按位或操作](https://leetcode.cn/problems/bitwise-ors-of-subarrays/)
- [1521. 找到最接近目标值的函数值](https://leetcode.cn/problems/find-a-value-of-a-mysterious-function-closest-to-target/)
- [6201. 找出前缀异或的原始数组](https://leetcode.cn/problems/find-the-original-array-of-prefix-xor/)
- [2506. 统计相似字符串对的数目](https://leetcode.cn/problems/count-pairs-of-similar-strings/)
- 剑指 Offer II 001. 整数除法
- 面试题 05.01. 插入
- 面试题 05.02. 二进制数转字符串
- 面试题 05.03. 翻转数位
- 面试题 05.06. 整数转换
- 面试题 05.07. 配对交换
- 面试题 05.08. 绘制直线
- 面试题 08.05. 递归乘法
136. 只出现一次的数字
class Solution {
public int singleNumber(int[] nums) {
int res = 0;
for (Integer i : nums) res ^= i;
return res;
}
}
137. 只出现一次的数字 II
使用位运算 (x >> i) & 1 得到 x 的第 i 个二进制位,并将它们相加再对 3 取余,得到的结果一定为 0 或 1,即为答案的第 i 个二进制位。
如果使用的语言对「有符号整数类型」和「无符号整数类型」没有区分,那么可能会得到错误的答案。这是因为「有符号整数类型」(即 int 类型)的第 31 个二进制位(即最高位)是补码意义下的符号位,对应着 − 2 31 -2^{31} −231 ,而「无符号整数类型」由于没有符号,第 31 个二进制位对应着 2 31 2^{31} 231 。Python 中需要对最高位进行特殊判断。
class Solution:
def singleNumber(self, nums: List[int]) -> int:
ans = 0
for i in range(32):
total = sum((num >> i) & 1 for num in nums)
if total % 3:
# Python 这里对于最高位需要特殊判断
if i == 31:
ans -= (1 << i)
else:
ans |= (1 << i)
return ans
260. 只出现一次的数字 III
def singleNumber(self, nums: List[int]) -> List[int]:
xor = 0
for i in nums:
xor ^= i
lb = xor & -xor # 最右侧 1,用于分组。
x = y = 0
for i in nums:
if lb & i:
x ^= i
else:
y ^= i
return [x, y]
191. 位1的个数
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int ans = 0;
while(n != 0) {
n &= n - 1; // 去除低位的 1
ans++;
}
return ans;
}
}
201. 数字范围按位与
class Solution {
public int rangeBitwiseAnd(int left, int right) {
// 最大值 + 1 = 最小值,所以条件还成立。
右边界 n 是 2147483647,也就是 Integer 中最大的正数,二进制形式是 01111...1,其中有 31 个 1。当 i 等于 n 的时候依旧会进入循环。出循环执行 i++,我们期望它变成 2147483647 + 1 = 2147483648,然后跳出 for 循环。事实上,对 2147483647 加 1,也就是 01111...1 加 1,变成了 1000..000,其中有 31 个 1。而这个二进制在补码中表示的是 -2147483648。
// 2147483646 2147483647 输出:0
// int ans = Integer.MAX_VALUE;
// for(int i = left; i <= right; i++){
// ans &= i;
// if(ans == 0) return 0;
// }
// return ans;
// left 要赋值给 i,所以提前判断一下
// 2147483647 2147483647 输出:0
// if(left == Integer.MAX_VALUE) return left;
// int res = left;
// for (int i = left + 1; i <= right; i++) {
// res &= i;
// if(res == 0 || i == Integer.MAX_VALUE) break;
// }
// return res;
// 计算 left 到 right 的最长公共前缀
// int i = 0;
// while(left < right){
// left >>= 1; // 移去不同部分
// right >>= 1;
// i++;
// }
// return left << i;
// 去掉最右端的 1,直到相等。
// while(right > left){
// right &= right - 1;
// }
// return right;
if (left == right) return left;
return left & ~Integer.highestOneBit(left ^ right) + 1;
// return left == right ? left : left & -Integer.highestOneBit(left ^ right);
}
}
面试题 17.01. 不用加号的加法
两数 a, b 相加,不考虑进位和为 a ^ b,进位 (a & b) << 1,结果为 (a ^ b),((a & b) << 1) 的和。递归结束条件 (a & b) << 1 == 0。
class Solution {
public int add(int a, int b){
if(b == 0) return a;
return add(a ^ b, (a & b) << 1);
}
}
两个数 a, b 相加,如果 (a & b) << 1 为零没有进位,否则,add(a, b) = (a ^ b) ^ ( (a & b) << 1 )。
class Solution {
public int add(int a, int b) {
while(b != 0){
int carry = (a & b) << 1;
a ^= b;
b = carry;
}
return a;
}
}
67. 二进制求和
class Solution:
def addBinary(self, a: str, b: str) -> str:
x, y = int(a, 2), int(b, 2)
while y:
x, y = x ^ y, (x & y) << 1
return bin(x)[2:]
# return bin(int(a, 2) + int(b, 2))[2:]
# return '{:b}'.format(int(a, 2) + int(b, 2))
计算当前 x 和 y 的无进位相加结果:answer = x ^ y
计算当前 x 和 y 的进位:carry = (x & y) << 1
完成本次循环,更新 x = answer,y = carry
import java.math.BigInteger;
class Solution {
public String addBinary(String a, String b) {
// BigInteger x = new BigInteger(a, 2), y = new BigInteger(b, 2);
// return x.add(y).toString(2);
StringBuffer ans = new StringBuffer();
int m = a.length(), n = b.length(), k = Math.max(m, n), carry = 0;
for (int i = 0; i < k; ++i) {
carry += i < m ? (a.charAt(m - 1 - i) - '0') : 0;
carry += i < n ? (b.charAt(n - 1 - i) - '0') : 0;
ans.append((char) (carry % 2 + '0'));
carry /= 2;
}
if (carry > 0) ans.append('1');
return ans.reverse().toString();
}
}
190. 颠倒二进制位
方法一:逐位颠倒
将 n 视作一个长为 32 的二进制串,从低位往高位枚举 n 的每一位,将其倒序添加到翻转结果
rev
textit{rev}
rev 中。
每枚举一位就将 n 右移一位,这样当前 n 的最低位就是要枚举的比特位。当 n 为 0 时即可结束循环。
class Solution:
def reverseBits(self, n: int) -> int:
# rev = 0
# for i in range(32):
# if n != 0:
# # n 的二进制末尾数字,拼接到 res 的开头,移动的是 n 的末尾数字。
# rev |= (n & 1) << (31 - i)
# n >>= 1
# return rev
res = 0
for i in range(32):
# res 左移,把 n 的二进制末尾数字,拼接到结果 res 的末尾。然后 n 右移。
res = (res << 1) | (n & 1)
n >>= 1
return res
231. 2 的幂
class Solution:
def isPowerOfTwo(self, n: int) -> bool:
return not n & (n - 1) and n > 0
return n & (-n) == n
268. 丢失的数字
class Solution:
def missingNumber(self, nums: List[int]) -> int:
## 方法一:排序
# n = len(nums)
# nums.sort()
# for i in range(n):
# if nums[i] != i:
# return i
# return n
## 方法二:哈希表
# hash = set(nums)
# for i in range(len(nums) + 1):
# if i not in hash:
# return i
## 方法三:差
# return sum(range(len(nums) + 1)) - sum(nums)
# return (n := len(nums)) * (n + 1) // 2 - sum(nums)
## 方法四:异或
res = 0
for i, num in enumerate(nums):
res ^= i ^ num
res ^= len(nums)
return res
318. 最大单词长度乘积
words[i] 用一个32 位二进制的数字表示,二进制位第 [0, 25] 位,分别对应 [a, z],利用位运算的判断两个字符 words[i] 和 words[j] 是否有公共字母。
转换: abd => 00000…1011 => 11(10进制的11)
判断公共字母: abd & b => 1011 & 0010 != 0
方法一:set
class Solution:
def maxProduct(self, words: List[str]) -> int:
s = [set(w) for w in words]
ans, n = 0, len(words)
for i in range(n):
for j in range(i + 1, n):
if not s[i] & s[j]:
ans = max(ans, len(words[i]) * len(words[j]))
return ans
方法二:位运算
class Solution:
def maxProduct(self, words: List[str]) -> int:
res, n = 0, len(words)
wordArr = [0] * n
for i, word in enumerate(words):
for ch in set(word):
wordArr[i] |= (1 << (ord(ch)-ord('a')))
for i in range(n):
for j in range(i + 1, n):
if (wordArr[i] & wordArr[j]) == 0:
res = max(res, len(words[i]) * len(words[j]))
return res
## reduce 列表推导式
masks = [reduce(lambda a, b: a | (1 << (ord(b) - ord('a'))), word, 0) for word in words]
return max((len(x[1]) * len(y[1]) for x, y in product(zip(masks, words), repeat=2) if x[0] & y[0] == 0), default=0)
class Solution:
def maxProduct(self, words: List[str]) -> int:
def hashset(word):
# 用 32 位二进制数表示 word,也就是将 字符串影射 到 数字
# | 只计算不重复字母的和,sum 是所有字母的和,"abc" 和 "aaac" sum 一样都是 7
return sum(1 << (ord(c) - ord('a')) for c in set(word))
d, ans = defaultdict(int), 0
for w in words:
h = hashset(w)
if d[h] < len(w):
for other in d:
if not other & h:
ans = max(ans, d[other] * len(w))
d[h] = len(w)
return ans
389. 找不同
方法一:计数
class Solution:
def findTheDifference(self, s: str, t: str) -> str:
d = {}
for c in s:
d[c] = d.get(c, 0) + 1
for c in t:
d[c] = d.get(c, 0) - 1
if d[c] < 0:
return c
class Solution:
def findTheDifference(self, s: str, t: str) -> str:
d = {}
for c in s + t:
d[c] = d.get(c, 0) + 1
return [x for x in d if d[x]%2][-1]
方法二:求和
class Solution:
def findTheDifference(self, s: str, t: str) -> str:
return chr(sum(ord(c) for c in t) - sum(ord(c) for c in s))
# 利用 Counter (标准库的 collections)
# return list(Counter(t) - Counter(s))[0]
方法三:位运算
class Solution:
def findTheDifference(self, s: str, t: str) -> str:
res = 0
for c in s + t:
res ^= ord(c)
return chr(res)
# return chr(reduce(xor, map(ord, s + t)))
方法四:列表排序
class Solution:
def findTheDifference(self, s: str, t: str) -> str:
s = list(s)
t = list(t)
s.sort()
t.sort()
for i in range(len(s)):
if s[i] != t[i]:
return t[i]
return t[-1]
397. 整数替换
方法一:记忆化搜索
class Solution:
@cache # 记忆化搜索
def integerReplacement(self, n: int) -> int:
if n == 1: return 0
if n & 1: # 奇数 加减后除以 2 共两次操作
return 2 + min(self.integerReplacement((n - 1) >> 1), self.integerReplacement((n + 1) >> 1))
return 1 + self.integerReplacement(n >> 1)
方法二:贪心
递归枚举中的「最优解」是固定的。
if n <= 3:return n - 1
偶数
奇数 n % 4 余数为 1 或 3,减一或加一
class Solution:
def integerReplacement(self, n: int) -> int:
res = 0
while n != 1:
if n & 1:
n += -1 if n & 2 == 0 or n == 3 else 1
else:
n >>= 1
res += 1
return res
## 递归
# @lru_cache(None)
def x(n):
if n <= 3: return n - 1
if n & 1 == 0: return 1 + x(n >> 1)
if n & 4 == 1:
return 3 + x((n - 1) >> 2)
return 3 + x((n + 1) >> 2)
return x(n)
405. 数字转换为十六进制数
方法一:位运算
题目要求将给定的整数 num 转换为十六进制数,负整数使用补码运算方法。
在补码运算中,最高位表示符号位,符号位是 0 表示正整数和零,符号位是 1 表示负整数。32 位有符号整数的二进制数有 32 位,由于一位十六进制数对应四位二进制数,因此 32 位有符号整数的十六进制数有 8 位。将 num 的二进制数按照四位一组分成 8 组,依次将每一组转换为对应的十六进制数,即可得到 num 的十六进制数。
假设二进制数的 8 组从低位到高位依次是第 0 组到第 7 组,则对于第 i 组,可以通过 (num >> (4×i)) & 0xf 得到该组的值,其取值范围是 0 到 15(即十六进制的 f)。将每一组的值转换为十六进制数的做法如下:
对于 0 到 9,数字本身就是十六进制数;对于 10 到 15,将其转换为 a 到 f 中的对应字母。
对于负整数,由于最高位一定不是 0,因此不会出现前导零。对于零和正整数,可能出现前导零。避免前导零的做法如下:
如果 num = 0,则直接返回 0;
如果 num > 0,则在遍历每一组的值时,从第一个不是 0 的值开始拼接成十六进制数。
计算机存储 32 位有符号整数。int 型整数存储范围在 [ − 2 31 , 2 31 − 1 ] [-2^{31}, 2^{31} - 1] [−231,231−1] 内,且在计算机内部以补码形式表示,共 32 位,最高位为符号位,负数符号位为 1,正数为 0。
在计算机中, [ 0 , 2 31 − 1 ] [0, 2^{31} - 1] [0,231−1] 范围内的数对应的十六进制存储方式为 0x00000000-0x7FFFFFFF,(0 - 2147483647), [ − 2 31 , − 1 ] [-2^{31},-1] [−231,−1] 范围内的数对应的十六进制存储方式为 0x80000000-0xFFFFFFFF$。(2147483648 - 4294967295)
可以先将负数统一加上 2 32 2^{32} 232,使其映射到 [ 2 31 , 2 32 − 1 ] [2^{31}, 2^{32} - 1] [231,232−1] 范围内,就可以直接进行十六进制转换了。
负数加上 232 其实就是负数的绝对值取补数 232 - abs(num)
也可以通过与运算 &,或模运算 %,统一正负数。
num & 0xffffffff # 余数 num % (2 ** 32 )
print(0xffffffff,2 ** 32 - 1) # 4294967295 4294967295
num & 0xffffffff 这步操作将负数转换为正数,而这个正数的二进制编码正好和 32 位的负数的二进制编码一样,但是对其进行操作却没有对负数的二进制操作那么多限制。
为了方便起见,我们提前将十六进制对应的 16 种不同字符存到字符串 s 中,方便进制转换过程中直接提取。
输入为 0 时,直接返回 “0” ;
输入为正数时,通过不断求余数,最后翻转字符串得到十六进制表示;
输入为负数时,利用补码运算的方法,计算其补码运算后的数字,按正数步骤处理,最后处理符号位,注意,输入负数最小值时,补码运算后为 0 ,与输入为 0 要区分,特殊处理。
class Solution:
def toHex(self, num: int) -> str:
lib, ret = "0123456789abcdef", ""
# 加上 2**32 负数取补数 2**32 - abs(num)
# 1 << 32 = 2 ** 32 = -1 & 0xffffffff + 1 = 4294967296
# n = num + (1 << 32) if num < 0 else num
n = num & 0xffffffff # 余数 num % (2 ** 32 - 1)
if n == 0: return "0"
while n:
# ret = lib[n % 16] + ret
# n //= 16
ret = lib[n & 0xf] + ret # 掩码 0X0000000F -> 15
n >>= 4
return ret
458. 可怜的小猪
特别经典的一道题,1024个桶里,有一个有毒,十个小白鼠可以做测试,怎么一次找到有毒的那个?
将 0~1023 写成二进制,最多是十位,每个小白鼠喝所有某一位为 1 的(一鼠一位)
最终要找的那个就是所有死的小白鼠的位为 1,其他位为 0
十只小白鼠一次可以试出 2^10 个桶,如果是两次呢?
其实两次可以看成三进制,每个小白鼠可以在两轮内试出某一位是 0 还是 1 还是 2
第一次死就是那一位为 1,第二次是那一次为 2,没死就是那一位为 0
这样来看的话,x 轮就该转换成(x + 1)进制, 要找 buckets 在 x + 1 进制下是几位,就是我们至少需要的小白鼠个数了。
class Solution:
def poorPigs(self, buckets: int, minutesToDie: int, minutesToTest: int) -> int:
return ceil(log(buckets, minutesToTest//minutesToDie + 1))
476. 数字的补数
方法一:位运算
找二进制 num 中最高位是 1 的位数 i,然后遍历 num 的第 0 ∼ i 0∼i 0∼i 个二进制位,将它们依次进行取反。可以构造掩码 m a s k = 2 i + 1 − 1 mask = 2^{i+1} - 1 mask=2i+1−1,将 num 与 mask 进行异或运算。
class Solution:
def findComplement(self, num: int) -> int:
for i in range(1, 30 + 1):
if num < (1 << i): break
else: i = 31
# i - 1 是 num 二进制位中最高位是 1 的位数
mask = (1 << i) - 1
return num ^ mask
那怎么获取得与 num 二进制同样长度的 1 呢?
- 按位找最前边的 1;
- 利用 -1 的补码就是全1的(~0 也可以)。然后根据 mask 与 num 相与,判断 mask 的右移是否到位,如果有重合,那一定相与结果会不等于零!
class Solution {
public int findComplement(int num) {
mask = -1 # 0xFFFFFFFF 即全为 1 补码
while (mask & num) > 0:
mask <<= 1
return ~mask ^ num
剑指 Offer II 003. 前 n 个数字二进制中 1 的个数
class Solution {
public int[] countBits(int n) {
int[] ans = new int[n + 1];
int highBit = 0;
for(int i = 1; i < n + 1; i++) {
// ans[i] = Integer.bitCount(i);
// ans[i] = bit1(i);
// ans[i] = bit2(i);
ans[i] = ans[i & (i - 1)] + 1;
// ans[i] = ans[i >> 1] + (i & 1); // 最低位 1,右移分奇偶。
// 记录 i 的最高 bit 位。最高位 1
// if ((i & (i - 1)) == 0) highBit = i;
// ans[i] = ans[i - highBit] + 1;
}
return ans;
}
int bit1(int x){
int res = 0;
while(x > 0){
res += x % 2; x /= 2;
}
return res;
}
int bit2(int x){
int res = 0;
while(x > 0){
x &= x - 1; res++;
}
return res;
}
}
89. 格雷编码
格雷码,又叫循环二进制码或反射二进制码,格雷码是我们在工程中常会遇到的一种编码方式,它的基本的特点就是任意两个相邻的代码只有一位二进制数不同。
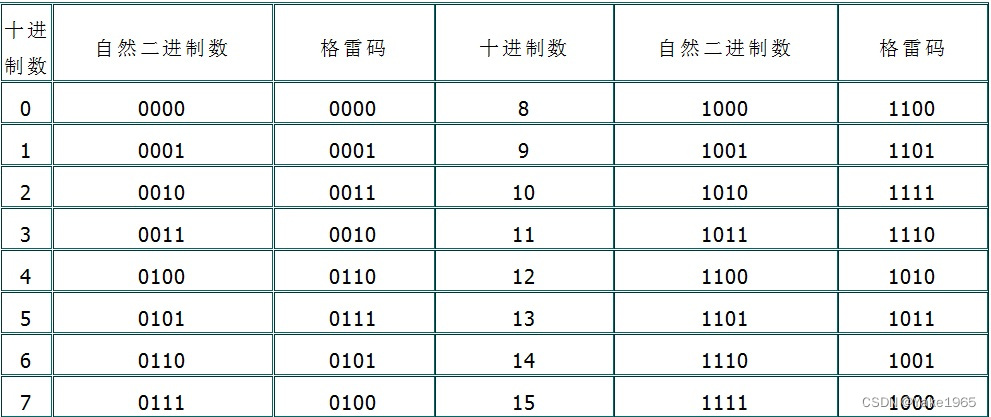
1、二进制码转换成格雷码
法则是保留二进制码的最高位作为格雷码的最高位;次高位格雷码为二进制码的高位与次高位相异或,其余各位类似。
2、格雷码转换成二进制码
法则是保留格雷码的最高位作为自然二进制码的最高位;次高位自然二进制码为高位自然二进制码与次高位格雷码相异或,其余各位类似。
自然数与格雷码位数必然相同,Gi表示格雷码第i位,Bi表示自然数第i位,相互转换定义如下:
自然数转换成格雷码
转换关系为:Gi = Bi ^ B(i+1),【当 i == 最高位时,i+1位是0】
格雷码转换成自然数
转换关系为:Bi = Gi ^ B(i+1),【当i == 最高位时,i+1位是0】
class Solution {
public List<Integer> grayCode(int n) {
List<Integer> res = new ArrayList<>();
for(int i = 0; i < 1 << n; ++i)
res.add(i ^ i >> 1);
return res;
}
}
1611. 使整数变为 0 的最少操作次数
class Solution {
public int minimumOneBitOperations(int n) {
int ans = 0;
while (n > 0) {
ans ^= n;
n >>= 1;
}
return ans;
}
}
1318. 或运算的最小翻转次数
class Solution {
public int minFlips(int a, int b, int c) {
int ans = 0;
for(int i = 0; i < 32; i++){
int x = a >> i & 1, y = b >> i & 1, z = c >> i & 1;
if((x | y) != z){
if(z == 0) ans += x + y;
else ans++;
}
}
return ans;
}
}
6169. 最长优雅子数组
class Solution:
def longestNiceSubarray(self, nums: List[int]) -> int:
ans = left = mask = 0
for i, x in enumerate(nums):
# (a^b)&c = a&c^b&c 分配率
while mask & x: # 说明每个数 y, x & y != 0
mask ^= nums[left]
left += 1
mask ^= x
ans = max(ans, i - left + 1)
return ans
剑指 Offer 15. 二进制中1的个数
剑指 Offer 65. 不用加减乘除做加法
数组中两个数的最大异或值
重复的DNA序列
最大单词长度乘积
1238. 循环码排列
1442. 形成两个异或相等数组的三元组数目
1486. 数组异或操作
1611. 使整数变为 0 的最少操作次数
1655. 分配重复整数
1659. 最大化网格幸福感
1707. 与数组中元素的最大异或值
1723. 完成所有工作的最短时间
1815. 得到新鲜甜甜圈的最多组数
1835. 所有数对按位与结果的异或和
1863. 找出所有子集的异或总和再求和
1947. 最大兼容性评分和
2044. 统计按位或能得到最大值的子集数目
2172. 数组的最大与和
2220. 转换数字的最少位翻转次数
2275. 按位与结果大于零的最长组合
2317. 操作后的最大异或和
29. 两数相除
338. 比特位计数
393. UTF-8 编码验证
401. 二进制手表
405. 数字转换为十六进制数
461. 汉明距离
464. 我能赢吗
477. 汉明距离总和
693. 交替位二进制数
751. IP 到 CIDR
762. 二进制表示中质数个计算置位
810. 黑板异或游戏
898. 子数组按位或操作
982. 按位与为零的三元组
995. K 连续位的最小翻转次数
2411. 按位或最大的最小子数组长度
class Solution:
def smallestSubarrays(self, nums: List[int]) -> List[int]:
n = len(nums)
# 方法一:
# 每个数不超过30位,逆序计算每个数索引对 1 的贡献值。
#q = [0] * 30
q = defaultdict(int)
ans = [0] * n
for i in range(n-1,-1,-1):
for j in range(30):
if nums[i] >> j & 1:
q[j] = i # 更新索引
k = max(q.values(), default=i) # 需要的最大索引
ans[i] = k - i + 1
return ans
class Solution:
# 方法二:
ans = [1] * len(nums)
for i, x in enumerate(nums):
for j in range(i - 1, -1, -1):
if (nums[j] | x) == nums[j]: break
nums[j] |= x # 前缀或
ans[j] = i - j + 1 # 边走边看,最终才能确定值。截止到 i 的答案,后面会动态更新。
return ans
26. 删除有序数组中的重复项
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
left, n = 1, len(nums)
for i in range(1, n):
if nums[i] != nums[i - 1]:
nums[left] = nums[i]
left += 1
return left
898. 子数组按位或操作
class Solution:
def subarrayBitwiseORs(self, arr: List[int]) -> int:
ans, cur = set(), set()
for x in arr:
cur = {x | y for y in cur}
cur.add(x)
ans.update(cur)
return len(ans)
1521. 找到最接近目标值的函数值
class Solution:
def closestToTarget(self, arr: List[int], target: int) -> int:
ans = abs(arr[0] - target)
q = {arr[0]}
for num in arr:
q = {x & num for x in q} | {num}
ans = min(ans, min(abs(x - target) for x in q))
return ans
# 以下为二分
ans, cur = set(), set()
for x in arr:
cur = {x & y for y in cur}
cur.add(x)
ans.update(cur)
a = sorted(ans)
i = bisect_left(a, target)
if i == 0: return a[0] - target
if i == len(a): return target - a[-1]
return min(target-a[i-1], a[i]-target)
6201. 找出前缀异或的原始数组
class Solution:
def findArray(self, pref: List[int]) -> List[int]:
return [(pref[i-1] if i else 0) ^ x for i, x in enumerate(pref)]
# 异或的性质:A ^ B = C 则 A ^ C = B, ans[i] = pref[i] ^ pref[i - 1]
ans = [pref[0]]
for i in range(1, len(pref)):
ans.append(pref[i - 1] ^ pref[i])
return ans
2506. 统计相似字符串对的数目
class Solution:
def similarPairs(self, words: List[str]) -> int:
ans, cnt = 0, Counter()
for s in words:
mask = 0
for c in s:
mask |= 1 << (ord(c) - ord('a'))
ans += cnt[mask]
cnt[mask] += 1
return ans
class Solution {
public int similarPairs(String[] words) {
int ans = 0;
Map<Integer, Integer> map = new HashMap();
for(String w : words){
int mask = 0;
for(char c : w.toCharArray()){
mask |= 1 << (c - 'a');
}
ans += map.getOrDefault(mask, 0);
map.merge(mask, 1, Integer::sum);
}
return ans;
}
}
剑指 Offer II 001. 整数除法
面试题 05.01. 插入
面试题 05.02. 二进制数转字符串
面试题 05.03. 翻转数位
面试题 05.06. 整数转换
面试题 05.07. 配对交换
面试题 05.08. 绘制直线
面试题 08.05. 递归乘法
-
比特位计数
-
4的幂
-
两整数之和
-
汉明距离
-
数字的补数
-
汉明距离总和
20、 526. 优美的排列
21、 1178. 猜字谜
22、 1711. 大餐计数
最后
以上就是善良苗条最近收集整理的关于位运算(Bit Operation)136. 只出现一次的数字137. 只出现一次的数字 II260. 只出现一次的数字 III191. 位1的个数201. 数字范围按位与面试题 17.01. 不用加号的加法67. 二进制求和190. 颠倒二进制位231. 2 的幂268. 丢失的数字318. 最大单词长度乘积389. 找不同397. 整数替换405. 数字转换为十六进制数458. 可怜的小猪476. 数字的补数剑指 Offer II 003. 前 n 个数字二进制中 1 的个数89. 格雷编码的全部内容,更多相关位运算(Bit内容请搜索靠谱客的其他文章。








发表评论 取消回复