LeetCode-面试题57 - II. 和为s的连续正数序列——滑动窗口

75 阅读 0 评论 50 点赞

我是靠谱客的博主老实保温杯，最近开发中收集的这篇文章主要介绍LeetCode-面试题57 - II. 和为s的连续正数序列——滑动窗口，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

在这里插入图片描述

滑动窗口的重要性质是：窗口的左边界和右边界永远只能向右移动，而不能向左移动。这是为了保证滑动窗口的时间复杂度是 O(n)O(n)。如果左右边界向左移动的话，这叫做“回溯”，算法的时间复杂度就可能不止 O(n)O(n)。

在这道题中，我们关注的是滑动窗口中所有数的和。当滑动窗口的右边界向右移动时，也就是 j = j + 1 ，窗口中多了一个数字 j，窗口的和也就要加上 j。当滑动窗口的左边界向右移动时，也就是 i = i + 1，窗口中少了一个数字 i，窗口的和也就要减去 i。滑动窗口只有 右边界向右移动（扩大窗口） 和 左边界向右移动（缩小窗口） 两个操作，所以实际上非常简单。

如何用滑动窗口解这道题

要用滑动窗口解这道题，我们要回答两个问题：

第一个问题，窗口何时扩大，何时缩小？
第二个问题，滑动窗口能找到全部的解吗？

对于第一个问题，回答非常简单：

当窗口的和小于 target 的时候，窗口的和需要增加，所以要扩大窗口，窗口的右边界向右移动
当窗口的和大于 target 的时候，窗口的和需要减少，所以要缩小窗口，窗口的左边界向右移动
当窗口的和恰好等于 target 的时候，我们需要记录此时的结果。设此时的窗口为 [i, j)[i,j)，那么我们已经找到了一个 ii
开头的序列，也是唯一一个 ii 开头的序列，接下来需要找 i+1i+1 开头的序列，所以窗口的左边界要向右移动

对于第二个问题，我们可以稍微简单地证明一下：
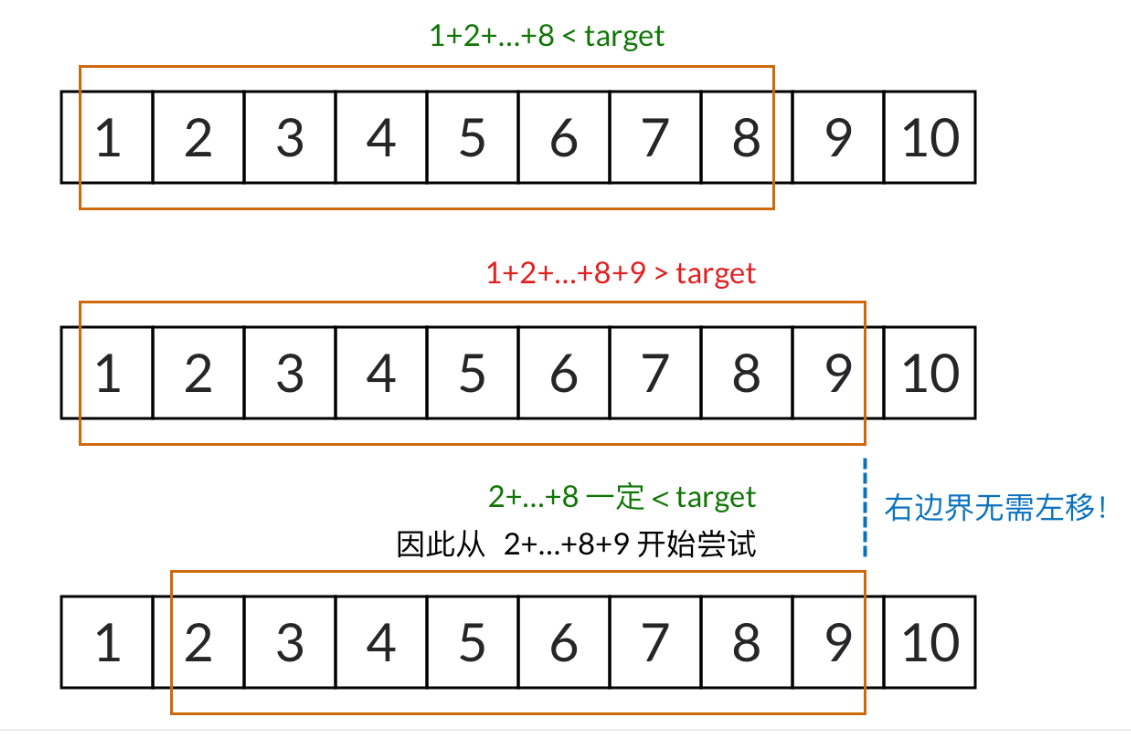
在这里插入图片描述
我们一开始要找的是 1 开头的序列，只要窗口的和小于 target，窗口的右边界会一直向右移动。假设 1+2+dots+81+2+⋯+8 小于 target，再加上一个 9 之后，发现 1+2+dots+8+91+2+⋯+8+9 又大于 target了。这说明 1 开头的序列找不到解。此时滑动窗口的最右元素是 9。

接下来，我们需要找 2 开头的序列，我们发现，2 + dots + 8 < 1 + 2 + dots + 8 < mathrm{target}2+⋯+8<1+2+⋯+8<target。这说明 2 开头的序列至少要加到 9。那么，我们只需要把原先 1~9 的滑动窗口的左边界向右移动，变成 2~9 的滑动窗口，然后继续寻找。而右边界完全不需要向左移动。

以此类推，滑动窗口的左右边界都不需要向左移动，所以这道题用滑动窗口一定可以得到所有的解。时间复杂度是 O(n)O(n)。

注：这道题当前可以用等差数列的求和公式来计算滑动窗口的和。不过我这里没有使用求和公式，是为了展示更通用的解题思路。实际上，把题目中的正整数序列换成任意的递增整数序列，这个方法都可以解。

class Solution {
    public int[][] findContinuousSequence(int target) {
    int i = 1; // 滑动窗口的左边界
    int j = 1; // 滑动窗口的右边界
    int sum = 0; // 滑动窗口中数字的和
    List<int[]> res = new ArrayList<>();

    while (i <= target / 2) {
        if (sum < target) {
            // 右边界向右移动
            sum += j;
            j++;
        } else if (sum > target) {
            // 左边界向右移动
            sum -= i;
            i++;
        } else {
            // 记录结果
            int[] arr = new int[j-i];
            for (int k = i; k < j; k++) {
                arr[k-i] = k;
            }
            res.add(arr);
            // 左边界向右移动
            sum -= i;
            i++;
            }
        }

        return res.toArray(new int[res.size()][]);
    }

}