前言

在本篇文章中，博主将讲解前面算法相关的练习题，还有双指针的相关方法。

一.快速选择算法（快速排序算法的延伸）

快速选择算法是一种与快速排序算法相似的算法，但是它的时间复杂度降为0（N），因为它每次都能根据实际情况只递归一边。下面让我们通过一道题来看看吧！

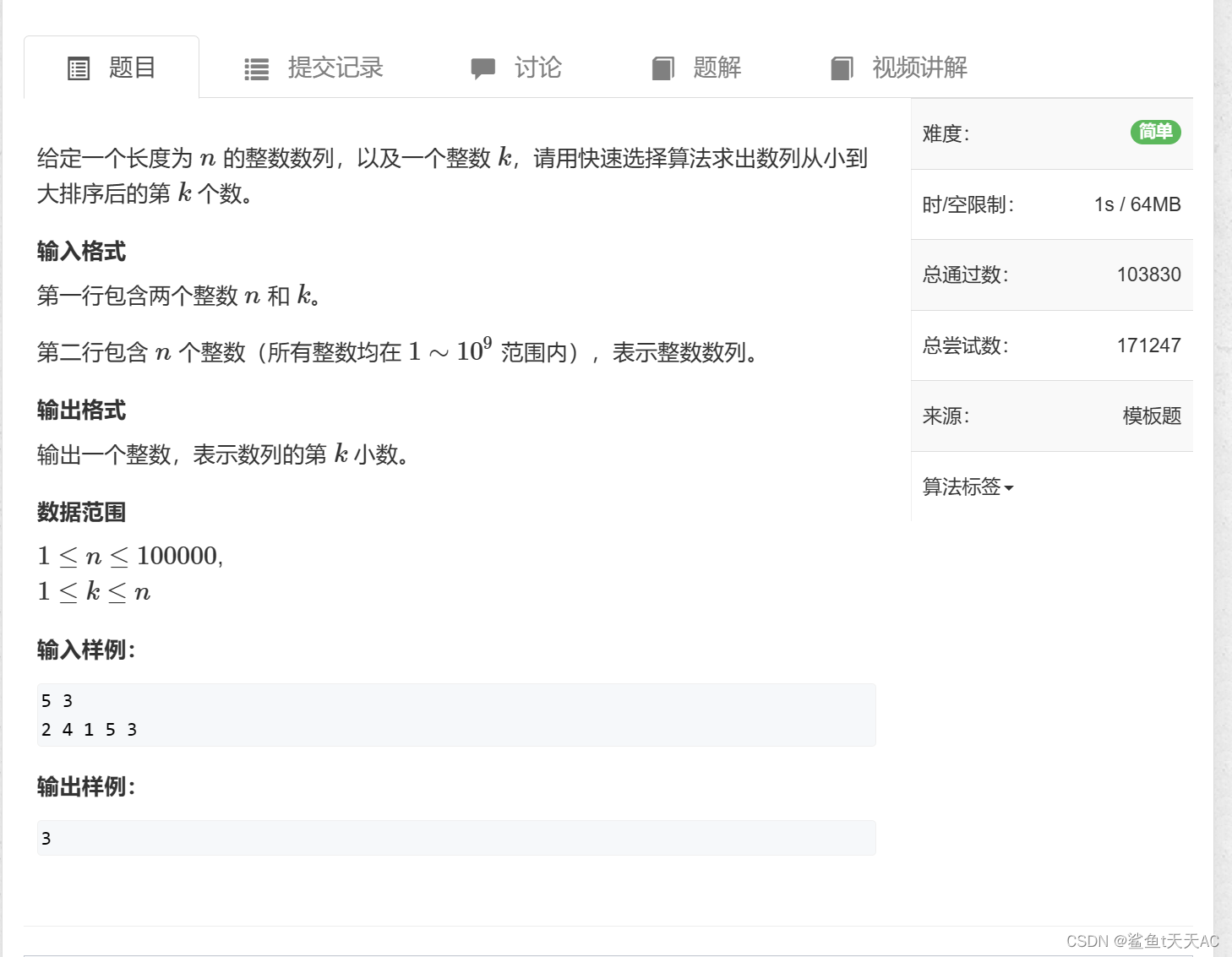
代码实现如下：

#include<iostream>
using namespace std;

const int N = 1e5+10;
int n,k;
int q[N];

int quick_sort(int l,int r,int k)
{
//这是base case，即最小规模子问题的处理
    if(l==r)    return q[l];
    int i = l-1,j = r+1,x = q[(l+r)/2];
    
    while(i<j)
    {
        do i++;while(q[i]<x);
        do j--;while(q[j]>x);
        if(i<j) swap(q[i],q[j]);
    }
    //计算左半边数组的长度。如果len>=k，说明我们要找的数在左半边，那么只要将左半边排序并返回第k小的值即可。如果len<k，说明我们要找的数在右半边，那么就要将右半边的数进行排序，并返回第（k-len）小的值。因为左半边的数<=右半边的数，因此这个值就是整个区间第k小的数。
    int len = j-l+1;
    if(k<=len)  return quick_sort(l,j,k);
    else    return  quick_sort(j+1,r,k-len); 
}

int main()
{
    scanf("%d%d",&n,&k);
    for(int i = 0;i<n;i++)  scanf("%d",&q[i]);
    
    cout<<quick_sort(0,n-1,k)<<endl;
}

我们可以发现，第一次我们需要处理的区间长度为n，第二次为n/2（这里的“/”表示除以，并不向下取整），第三次为n/4……那么加和后小于2n，因此该算法的时间复杂度为O（N）。

二、计算逆序对数量（归并排序的延伸）

逆序对是指：a、b两个数满足a>b，但b的位置在a之前。下面让我们学习一下如何求解逆序对的数量。

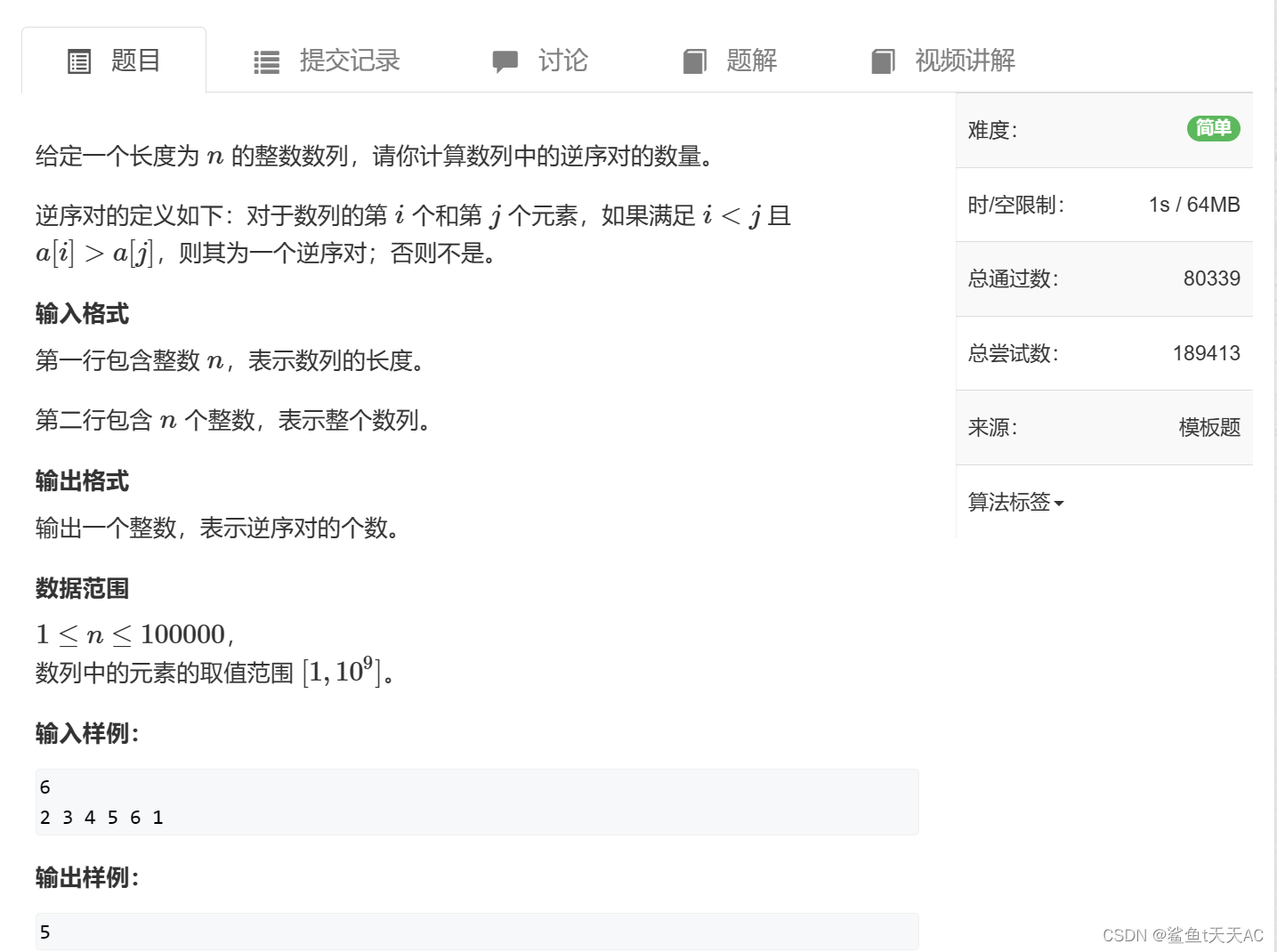
当左右两半部分排好序以后，逆序对的种类有三种：1.两个数都在左半边。2、两个数都在右半边。3.一个在左半边，一个在右半边。假设升级后（我们新定义）的归并排序函数能够返回逆序对的数量，那么对于1、2两种情况，只要分别递归左右部分并相加即可。那么第三种情况怎么处理呢？我们回忆一下归并排序的最后一步：把左右两部分数组按照大小顺序插入临时数组，再把临时数组的内容copy回原来的数组。我们的思路就可以是这样的：

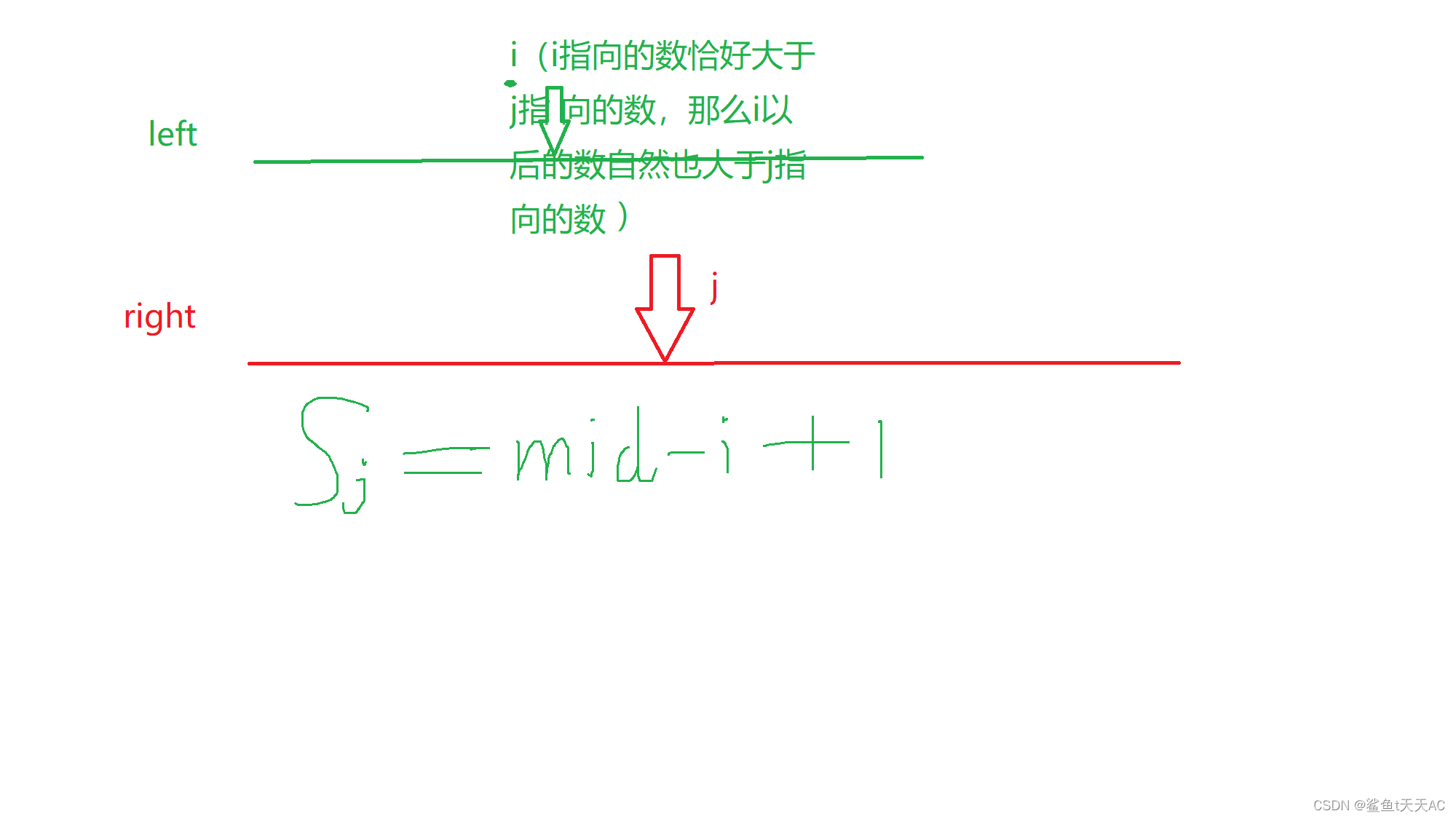
这里的Sj表示与j指向的数构成逆序对的left中数的个数。
那么三种情况我们都已经处理完啦！接下来看看代码吧！

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1e5 + 10;

int a[N], tmp[N];

LL merge_sort(int q[], int l, int r)
{
    if (l >= r) return 0;

    int mid = l + r >> 1;
    //先处理第1、2种情况
    LL res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r);
    //处理第三种情况
    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else
        {
            res += mid - i + 1;
            tmp[k ++ ] = q[j ++ ];
        }
    //若还有某个数组剩下一部分，直接接上就行
    //扫尾时不需要再让res增加，因为此时已经不存在数对了
    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
    

    return res;
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);

    cout << merge_sort(a, 0, n - 1) << endl;

    return 0;
}

//作者：yxc
//链接：https://www.acwing.com/activity/content/code/content/39791/
//来源：AcWing
//著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

三、双指针

双指针算法是一种依靠两个指针对数据结构进行操作的算法，我们熟知的归并排序中就用到了双指针算法。下面让我们通过一些例题来感受一下双指针算法的使用方式吧！

例题三、1 输出单词

这里有一些单词，它们之间以一个空格隔开，如abc def ghi。要求输出各个单词，每个单词占一行。这是一个比较简单的题目，但是它很好地体现了双指针的思想：

#include <iostream>
#include<string.h>
using namespace std;


int main()
{
    char str[100];
    
    gets[char];
    
    int n = strlen(str);
    
    for(int i = 0;i<n;i++)
    {
        //从i开始，寻找空格。
        int j = i;
        while(j<n&&str[j]!=' ') j++;
        //此时退出循环，j已经指向空格
        
        for(int k = i;k<j;k++)  cout<<str[k];
        cout<<endl;
        //下一次循环之前把j给i，那么进入循环后i++,i就自动指向空格后一个字母了。
        i = j;
    }
}

例题三、2最长连续不重复子序列

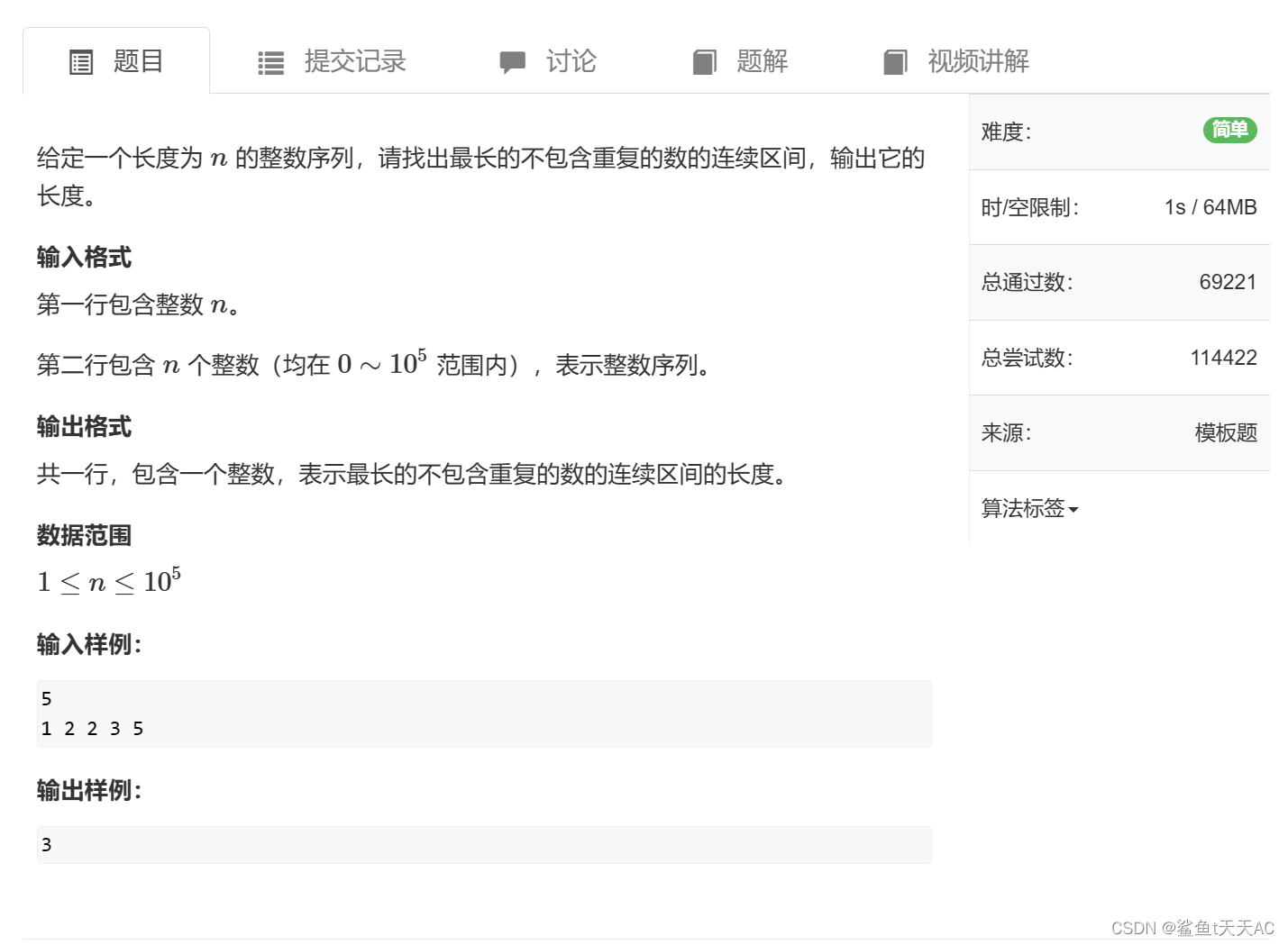
这道题该如何思考呢？我们创造i、j两个指示器，i在右边负责遍历数组，j在左边负责寻找离i最远的且j、i之间无重复数字的数，那么i、j之间长度的最大值就是我们要求的结果。图示如下：

那么根据这个思路，我们就知道i、j两个指针这样运动：i一直往前走，j从i处往后走，遇到重复的数就停下，每次更新最大长度。博主写的代码如下：

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
using namespace std;

const int N = 1e5 + 10;

int n;
int q[N];

//判断是否有重复元素
int check(int q[], int l, int r)
{
    for (int i = l; i <= r; i++)
    {
        for (int j = l; j < i; j++)
        {
            if (q[i] == q[j])  return 0;
        }
    }
    return 1;
}

int getMaxSunString(int q[], int n)
{
    //用max记录不重复连续子序列的最大长度
    int max = 0;
    for (int i = 0; i < n; i++)
    {
        //一定要小于等于！防止出现只有一个不重复的数字的情况！
        for (int j = 1; j<=i`在这里插入代码片`; j--)
        {
            if (check(q, j, i))
            {
                //当只有一个不重复的数字时如 2 2 2 2 2 2 2 1仍然适用。因为max全局变量初始值为0，i-j+1是大于max的。
                if (i - j + 1 > max)
                {
                    max = i - j + 1;
                }
            }
        }
    }
    return max;
}


int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i++)  scanf("%d", &q[i]);

    int res = getMaxSunString(q, n);
    
    cout<<res<<endl;
}

这段代码在Acwing上会造成Tine Limit Exceed，但是VS上测试成功。博主猜测是用了太多循环的原因。让我们看看yxc大佬是怎么做的吧！

#include <iostream>

using namespace std;

const int N = 100010;

int n;
int q[N], s[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    int res = 0;
    for (int i = 0, j = 0; i < n; i ++ )
    {
        //把q[i]出现的次数存到s数组对应q[i]下标处（q[i]是几就存到s的几下标处），每出现一次s对应下标处的值加一。
        s[q[i]] ++ ;
        //s[q[i]]>1说明前面有重复，如 4 4，那么后一个4的时候s[4] == 2，在前一个4处s[4] == 1。
        //在两种情况下while循环会停止：第一种是j==i而s[q[i]]>1，那么此时已经有重复，计数作废，i - j + 1 ==1.恰好只有一个不重复，符合实际；第二种是j<i而s[q[i]]<=1，说说明此时还没有重复，j停在上一次重复最后数字的下一个位置，i - j + 1也是对于此刻的i来说往左的最长不重复连续子串长度，符合实际。可能会有人认为按照逻辑关系量词运算还应该有j == i 且s[q[i]]<=1的情况，但这是不可能发生的，因为j == i之前循环已经因为s[q[i]]<=1停下！！！      
        while (j < i && s[q[i]] > 1) 
        //这里不能只写j++！这样写是为了让在i位置前出现的与i位置重复的数字所对应的s数组下标的值自减，否则会造成错判。比如说s[3]本来已经是1了，后面若再含有3，如果不把这个1减掉，会造成s[2]>1,从而j++（j<i的情况下）。但是实际上这里的2是前面的3而不是现在这个3造成的，j不应该++！！！
            s[q[j++]]--;
        //比较原有res和当前区间长度，把大的那个赋给res。
        res = max(res, i - j + 1);
    }

    cout << res << endl;

    return 0;
}

如果你想了解双指针算法在链表中的运用，可以看看这篇文章：
带你刷穿Leetcode链表OJ！

四、位运算

四、1：获得n二进制表示中第k位的方法

：（n>>k）&1（我们记最低位为第一位）

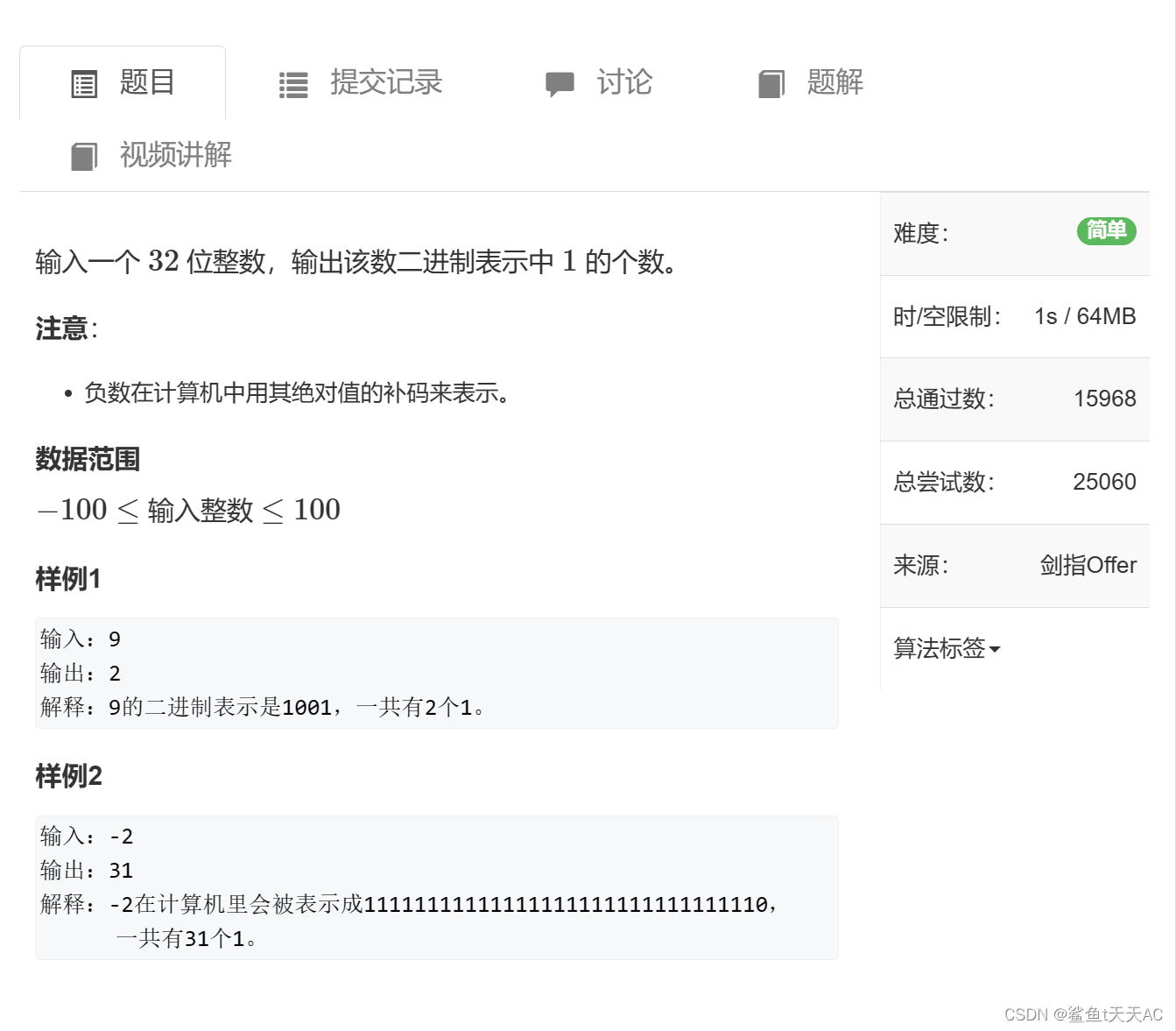
四、2：统计n二进制表示中1的个数

首先我们介绍一下lowbit，它可以返回二进制表示中最低位的1所表示的值。例如若某二进制数n为101010000，则lowbit（n）== 10000。lowbit（x）的实现方式如下：
x&（-x）
为什么这样就可以返回二进制中最低位的1所表示的值呢？我们来看看下面这张图就能理解了（这里需要原码、反码和补码的相关知识）——

#include<iostream>
using namespace std;

int lowbit(int x)
{
    return x&-x;
}

int main()
{
    int n = 0;
    cin>>n;
    
    while(n--)
    {
        int x = 0;
        cin>>x;
        
        int count = 0;
        
        while(x--)
        {
        //每次减去最低位的1表示的数值，知道减为零。
            x-= lowbit(x);
            count++;
        }
        
        cout<<count<<' ';
    }
    
    return 0;
}

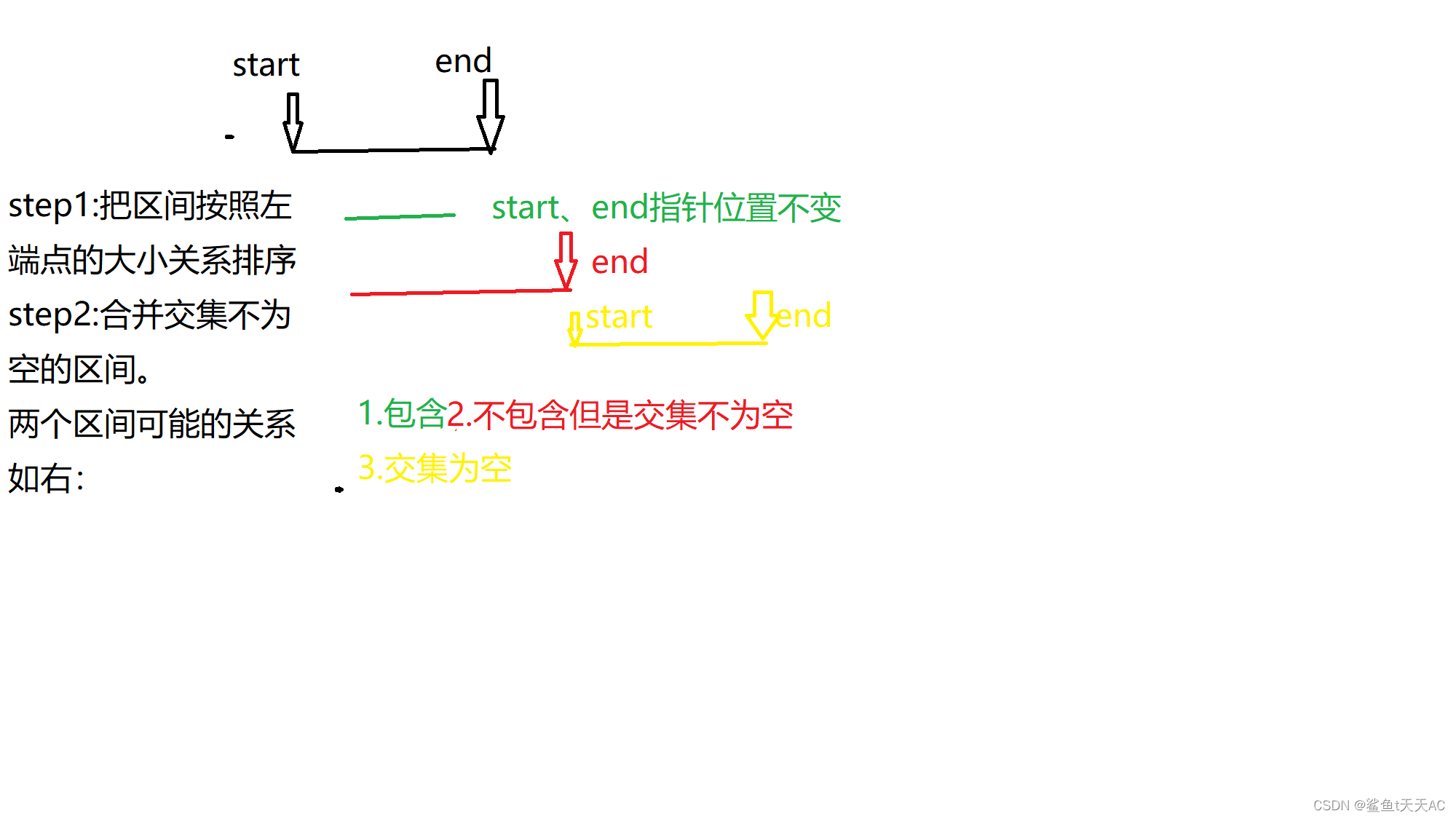
五、区间合并

这是一种合并交集不为空的区间的算法。如下题：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;
//用于存储两个数
typedef pair<int, int> PII;

void merge(vector<PII> &segs)
{
    //res是存储结果区间各个左右端点的数组
    vector<PII> res;
    //优先按照左端点排序，若左端点相同，再按照右端点排序。
    sort(segs.begin(), segs.end());
    //初始化，把范围扩大一些
    int st = -2e9, ed = -2e9;
    //遍历存左右端点的vector数组
    for (auto seg : segs)
    //交集为空的情况
        if (ed < seg.first)
        {
            if (st != -2e9) 
            //不要把最开始那个区间放进去！
                res.push_back({st, ed});
                //更新st与ed到下一个区间的左、右端点
                st = seg.first, ed = seg.second;
        }
        else ed = max(ed, seg.second);
    //包含和交集不为空但不包含的情况
    if (st != -2e9) res.push_back({st, ed});

    segs = res;
}

int main()
{
    int n;
    scanf("%d", &n);

    vector<PII> segs;
    //存入区间的左右端点
    for (int i = 0; i < n; i ++ )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        segs.push_back({l, r});
    }

    merge(segs);

    cout << segs.size() << endl;

    return 0;
}

// 作者：yxc
// 链接：https://www.acwing.com/activity/content/code/content/40108/
// 来源：AcWing
// 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

六、整数的保序离散化

考虑这样一些整数，它们的范围分布很大如1~1e9，但是个数较少，如1 ~ 1e5。离散化就是这样一个过程：把这些数映射到连续的数中（一般是从1开始的自然数，即数据对应的下标＋1。当然从零开始也OK）。如1 300 200000 4102030离散化后的结果是1 2 3 4。但是原数组中可能有重复元素，因此我们要去重。

对于这道题，我们要先离散化，再做前缀和（因为原始数据并不是紧挨着放置，直接前缀和的话无法确定步长）。

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

const int N = 300010;

int n, m;
int a[N], s[N];

vector<int> alls;
vector<PII> add, query;

int find(int x)
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1;
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++ )
    {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});

        alls.push_back(x);
    }

    for (int i = 0; i < m; i ++ )
    {
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});

        alls.push_back(l);
        alls.push_back(r);
    }

    // 去重
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());

    // 处理插入
    for (auto item : add)
    {
        int x = find(item.first);
        a[x] += item.second;
    }

    // 预处理前缀和
    for (int i = 1; i <= alls.size(); i ++ ) s[i] = s[i - 1] + a[i];

    // 处理询问
    for (auto item : query)
    {
        int l = find(item.first), r = find(item.second);
        cout << s[r] - s[l - 1] << endl;
    }

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/40105/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

bonus:unique函数的实现（对于已经排好序的序列，假设是升序）
如
1 2 2 3 5 5 5 6 7 9
我们开一个新数组来存放不重复的元素。这个不重复的元素应该满足一下两条中的一条：
1.它是第一个元素
2.a【i】! = a【i-1】。
只要满足其中之一，我们就把它存起来。为了达到这个目的，我们用双指针算法。一个指针用来遍历，另一个指针用来追踪。
代码实现（出自——）：
Acwing yxc

vector<int>::interator unique(vector<int>&a)
{
	//j用于记录新数组中已经有多少个元素
	int j = 0;
	for(int i = 0;i<a.size();i++)
	{
		if(!i||a[i]!=a[i-1])
		a[j++] = a[i];
	}
	return a.begin()+j;
}

好啦，以上就是本篇文章的全部内容。如果你感觉对你有帮助的话，请多多支持博主，你们的支持是我更新的最大动力哦！

最后

以上就是英勇可乐为你收集整理的小白也能学懂的XCPC第三站——习题课+双指针+位运算+离散化+区间合并。手把手教，萌新也能看懂的基础算法教程！前言二、计算逆序对数量（归并排序的延伸）三、双指针四、位运算五、区间合并六、整数的保序离散化的全部内容，希望文章能够帮你解决小白也能学懂的XCPC第三站——习题课+双指针+位运算+离散化+区间合并。手把手教，萌新也能看懂的基础算法教程！前言二、计算逆序对数量（归并排序的延伸）三、双指针四、位运算五、区间合并六、整数的保序离散化所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。