1、快速排序算法实现方式
快速排序的核心思想是分治法，分而治之。它的实现方式是每次从序列中选出一个基准值，其他数依次和基准值做比较，比基准值大的放右边，比基准值小的放左边，然后再对左边和右边的两组数分别选出一个基准值，进行同样的比较移动，重复步骤，直到最后都变成单个元素，整个数组就成了有序的序列。
简单概括如下：
-
从数列中挑出一个元素，称为 “基准”（pivot）;
-
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
-
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；
2、快速排序算法动画演示
3、图解快速排序算法
我们以[ 8，2，5，0，7，4，6，1 ]这组数字为例来进行演示
首先，我们随机选择一个基准值：
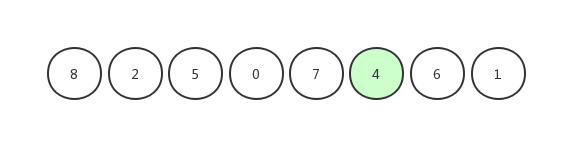
与其他元素依次比较，大的放右边，小的放左边：
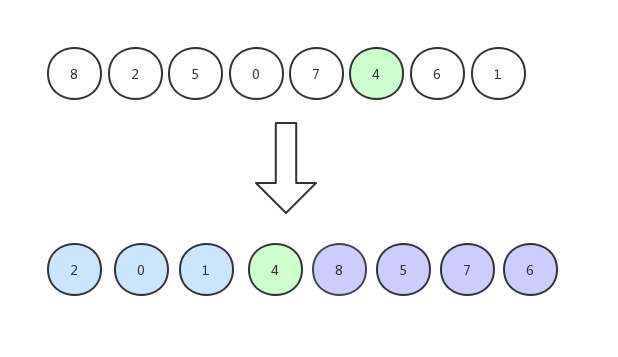
然后我们以同样的方式排左边的数据：
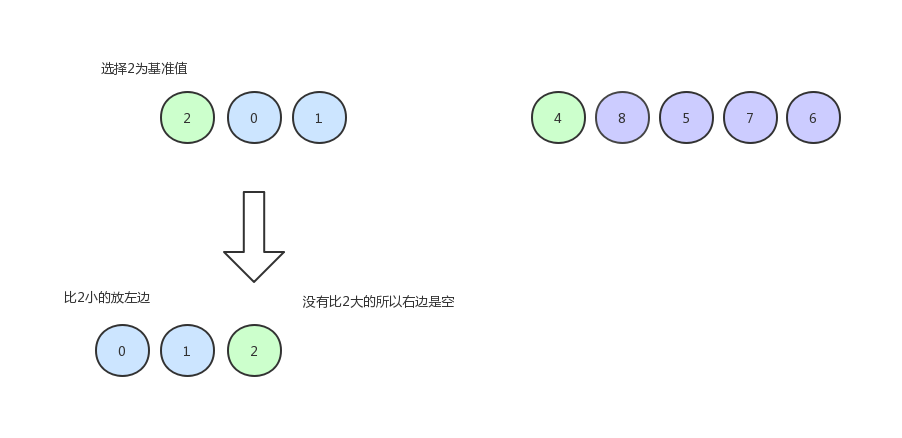
继续排 0 和 1 ：
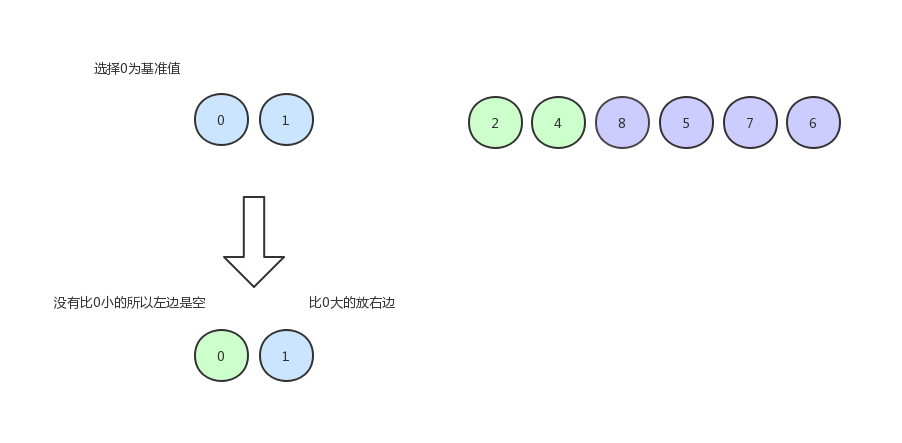
由于只剩下一个数，所以就不用排了，现在的数组序列是下图这个样子：
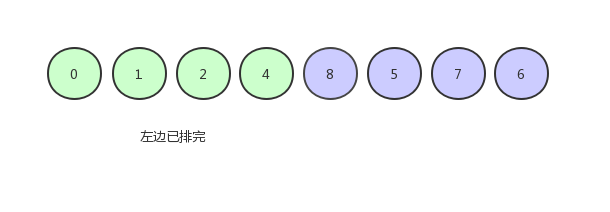
右边以同样的操作进行，即可排序完成。
4、快速排序算法Java代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
411//Java 代码实现 2public class QuickSort implements IArraySort { 3 4 @Override 5 public int[] sort(int[] sourceArray) throws Exception { 6 // 对 arr 进行拷贝，不改变参数内容 7 int[] arr = Arrays.copyOf(sourceArray, sourceArray.length); 8 9 return quickSort(arr, 0, arr.length - 1); 10 } 11 12 private int[] quickSort(int[] arr, int left, int right) { 13 if (left < right) { 14 int partitionIndex = partition(arr, left, right); 15 quickSort(arr, left, partitionIndex - 1); 16 quickSort(arr, partitionIndex + 1, right); 17 } 18 return arr; 19 } 20 21 private int partition(int[] arr, int left, int right) { 22 // 设定基准值（pivot） 23 int pivot = left; 24 int index = pivot + 1; 25 for (int i = index; i <= right; i++) { 26 if (arr[i] < arr[pivot]) { 27 swap(arr, i, index); 28 index++; 29 } 30 } 31 swap(arr, pivot, index - 1); 32 return index - 1; 33 } 34 35 private void swap(int[] arr, int i, int j) { 36 int temp = arr[i]; 37 arr[i] = arr[j]; 38 arr[j] = temp; 39 } 40 41}
5、单边扫描
快速排序的关键之处在于切分，切分的同时要进行比较和移动，这里介绍一种叫做单边扫描的做法。
我们随意抽取一个数作为基准值，同时设定一个标记 mark 代表左边序列最右侧的下标位置，当然初始为 0 ，接下来遍历数组，如果元素大于基准值，无操作，继续遍历，如果元素小于基准值，则把 mark + 1 ，再将 mark 所在位置的元素和遍历到的元素交换位置，mark 这个位置存储的是比基准值小的数据，当遍历结束后，将基准值与 mark 所在元素交换位置即可。
代码实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32public static void sort(int[] arr) { sort(arr， 0， arr.length - 1); } private static void sort(int[] arr， int startIndex， int endIndex) { if (endIndex <= startIndex) { return; } //切分 int pivotIndex = partitionV2(arr， startIndex， endIndex); sort(arr， startIndex， pivotIndex-1); sort(arr， pivotIndex+1， endIndex); } private static int partition(int[] arr， int startIndex， int endIndex) { int pivot = arr[startIndex];//取基准值 int mark = startIndex;//Mark初始化为起始下标 for(int i=startIndex+1; i<=endIndex; i++){ if(arr[i]<pivot){ //小于基准值 则mark+1，并交换位置。 mark ++; int p = arr[mark]; arr[mark] = arr[i]; arr[i] = p; } } //基准值与mark对应元素调换位置 arr[startIndex] = arr[mark]; arr[mark] = pivot; return mark; }
6、双边扫描
另外还有一种双边扫描的做法，看起来比较直观：我们随意抽取一个数作为基准值，然后从数组左右两边进行扫描，先从左往右找到一个大于基准值的元素，将下标指针记录下来，然后转到从右往左扫描，找到一个小于基准值的元素，交换这两个元素的位置，重复步骤，直到左右两个指针相遇，再将基准值与左侧最右边的元素交换。
我们来看一下实现代码，不同之处只有 partition 方法：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54public static void sort(int[] arr) { sort(arr， 0， arr.length - 1); } private static void sort(int[] arr， int startIndex， int endIndex) { if (endIndex <= startIndex) { return; } //切分 int pivotIndex = partition(arr， startIndex， endIndex); sort(arr， startIndex， pivotIndex-1); sort(arr， pivotIndex+1， endIndex); } private static int partition(int[] arr， int startIndex， int endIndex) { int left = startIndex; int right = endIndex; int pivot = arr[startIndex];//取第一个元素为基准值 while (true) { //从左往右扫描 while (arr[left] <= pivot) { left++; if (left == right) { break; } } //从右往左扫描 while (pivot < arr[right]) { right--; if (left == right) { break; } } //左右指针相遇 if (left >= right) { break; } //交换左右数据 int temp = arr[left]; arr[left] = arr[right]; arr[right] = temp; } //将基准值插入序列 int temp = arr[startIndex]; arr[startIndex] = arr[right]; arr[right] = temp; return right; }
7、极端情况
快速排序的时间复杂度和归并排序一样，O(n log n)，但这是建立在每次切分都能把数组一刀切两半差不多大的前提下，如果出现极端情况，比如排一个有序的序列，如[ 9，8，7，6，5，4，3，2，1 ]，选取基准值 9 ，那么需要切分 n - 1 次才能完成整个快速排序的过程，这种情况下，时间复杂度就退化成了 O(n2)，当然极端情况出现的概率也是比较低的。
所以说，快速排序的时间复杂度是 O(nlogn)，极端情况下会退化成 O(n2)，为了避免极端情况的发生，选取基准值应该做到随机选取，或者是打乱一下数组再选取。
另外，快速排序的空间复杂度为 O(1)。
我有一个微信公众号，经常会分享一些Java技术相关的干货；
如果你喜欢我的分享，可以用微信搜索“Java团长”或者“javatuanzhang”关注。
最后
以上就是大胆抽屉最近收集整理的关于快速排序算法动图演示及解析2021版（附Java代码实现）1、快速排序算法实现方式2、快速排序算法动画演示3、图解快速排序算法4、快速排序算法Java代码实现5、单边扫描6、双边扫描7、极端情况的全部内容，更多相关快速排序算法动图演示及解析2021版（附Java代码实现）1、快速排序算法实现方式2、快速排序算法动画演示3、图解快速排序算法4、快速排序算法Java代码实现5、单边扫描6、双边扫描7、极端情况内容请搜索靠谱客的其他文章。
发表评论 取消回复