概述
首先选一个基准 pivot，然后过一遍数组， 这样一来，这个 pivot 的位置就确定了，也就是排好了 1 个元素。 然后对 pivot 左边 ???? 的数排序， 那怎么排左边和右边？ 答：同样的方法。 所以快排也是用的分治法的思想。 选择一个 pivot，就把问题分成了 这两个问题。 就是最开始描述的方法，直到每个区间内没有元素或者只剩一个元素就可以返回了。 放在一起自然就是。 但是如何选择这个 pivot？ 取中间的？ 取第一个？ 取最后一个？ 比如选最后一个，就是 3. 然后我们就需要把除了 3 之外的数分成「比 3 大」和「比 3 小」的两部分，这个过程叫做 partition（划分）。 这里我们仍然使用「挡板法」的思想，不用真的弄两个数组来存这两部分，而是用两个挡板，把区间划分好了。 我们用「两个指针」（就是挡板）把数组分成「三个区间」，那么 那么初始化时，我们要保证「未排序区间」能够包含除了 3 之外的所有元素，所以 这样左边和右边的区间就成了： 注意 ⚠️ i, j 是不包含在左右区间里的呢。 那我们的目的是 check 未排序区间里的每一个数，然后把它归到正确的区间里，以此来缩小未排序区间，直到没有未排序的元素。 从左到右来 check： 5 > 3, 所以 5 要放在右区间里，所以 5 和 j 指向的 0 交换一下： 这样 5 就排好了，指针 j --，这样我们的未排序区间就少了一个数； 0 < 3，所以就应该在左边的区间，直接 i++； 2 < 3，同理，i++； 1 < 3，同理，i++； 所以当两个指针错位的时候，我们结束循环。 但是还差了一步，3 并不在正确的位置上呀。所以还要把它插入到两个区间中间，也就是和指针 i 交换一下。 齐姐声明：这里并不鼓励大家把 pivot 放最左边。 基本所有的书上都是放右边，既然放左右都是一样的，我们就按照大家默认的、达成共识的来，没必要去“标新立异”。 就比如围棋的四个星位，但是讲究棋道的就是先落自己这边的星位，而不是伸着胳膊去够对手那边的。 那当我们把 pivot 换回到正确的位置上来之后，整个 partition 就结束了。 之后就用递归的写法，对左右两边排序就好了。 最后还有两个问题想和大家讨论一下： 答：并不好。 因为我们是想把数组分割的更均匀，均匀的时间复杂度更低；但是如果这是一个有序的数组，那么总是取最后一个是最不均匀的取法。 所以应该随机取 pivot，这样就避免了因为数组本身的特点总是取到最值的情况。 随机选取之后，我们还是要把这个 pivot 放到整个数组的最右边，这样我们的未排序区间才是连续的，否则每次走到 pivot 这里还要想着跳过它，心好累哦。 这里的时空复杂度和分的是否均匀有很大关系，所以我们分情况来说： 如果每次都能差不多均匀分，那么 如果每次都能取到最大/最小值，那么递归树就变成了这个样子： 如上图所示：O(n^2) 这棵递归树的高度就变成了 O(n). 实际呢，大多数情况都会接近于均匀的情况，所以均匀的情况是一个 average case. 为什么看起来最好的情况实际上是一个平均的情况呢？ 因为即使如果没有取到最中间的那个点，比如分成了 10% 和 90% 两边的数，那其实每层的时间还是 O(n)，只不过层数变成了以 9 为底的 log，那总的时间还是 O(nlogn). 所以快排的平均时间复杂度是 O(nlogn)。 那你应该能看出来了，在 swap 的时候，已经破坏了元素之间的相对顺序，所以快排并不具有稳定性。 这也回答了我们开头提出的问题，就是 为什么对于 primitive type 使用快排， 为什么对于 object 使用归并， 以上就是快排的所有内容了，也是很常考的内容哦！那下一篇文章我会讲几道从快排引申出来的题目，猜猜是什么？???? 如果你喜欢这篇文章，记得给我点赞留言哦～你们的支持和认可，就是我创作的最大动力，我们下篇文章见！ 我是小齐，纽约程序媛，终生学习者，每天晚上 9 点，云自习室里不见不散！ 更多干货文章见我的 Github: https://github.com/xiaoqi6666/NYCSDE
快速排序
对 pivot 右边 ???? 的数排序，
就完成了。「分」
「治」
「合」
举个例子：{5, 2, 1, 0, 3}.
Step1.
Step2.
Step3.
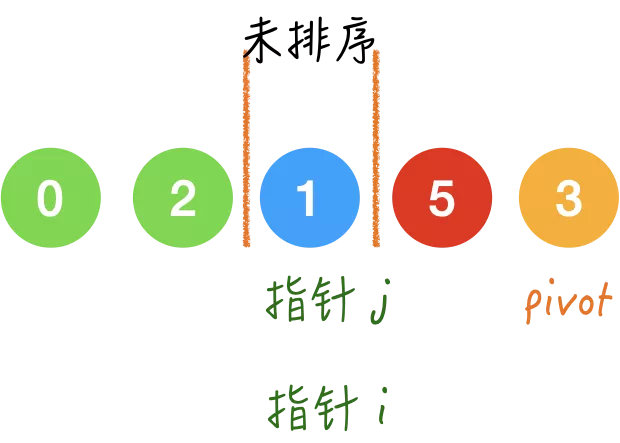
Step4.
class Solution {
public void quickSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
quickSort(array, 0, array.length - 1);
}
private void quickSort(int[] array, int left, int right) {
// base case
if (left >= right) {
return;
}
// partition
Random random = new Random(); // java.util 中的随机数生成器
int pivotIndex = left + random.nextInt(right - left + 1);
swap(array, pivotIndex, right);
int i = left;
int j = right-1;
while (i <= j) {
if (array[i] <= array[right]) {
i++;
} else {
swap(array, i, j);
j--;
}
}
swap(array, i, right);
//「分」
quickSort(array, left, i-1);
quickSort(array, i+1, right);
}
private void swap(int[] array, int x, int y) {
int tmp = array[x];
array[x] = array[y];
array[y] = tmp;
}
}1. 均分
时间复杂度
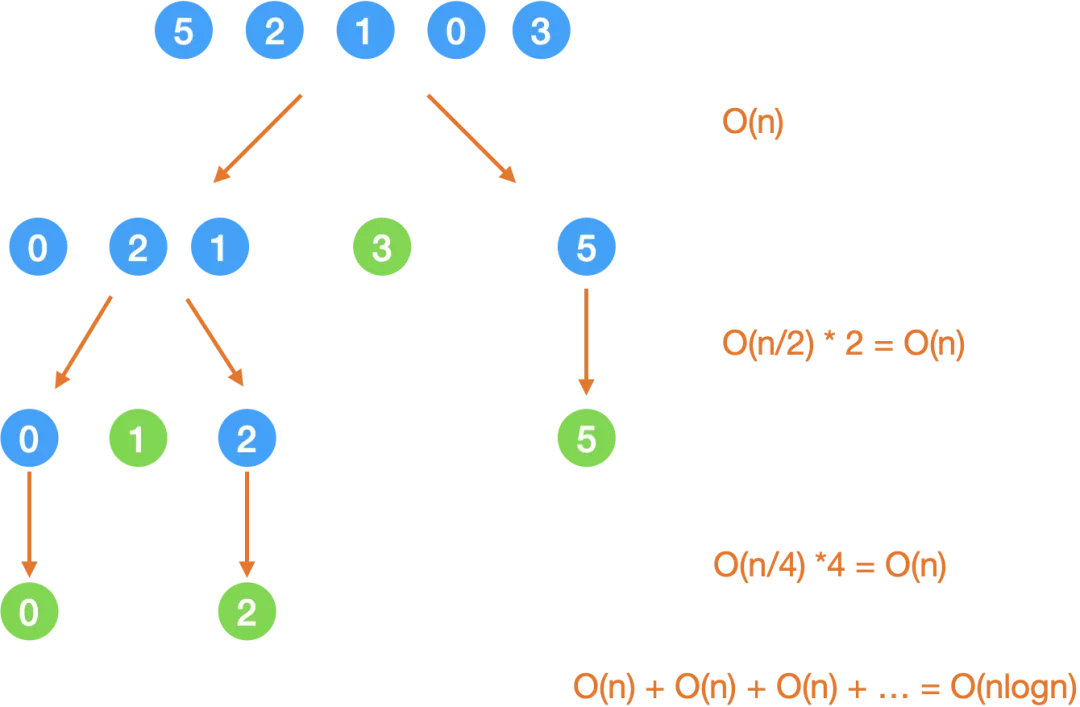
空间复杂度
2. 最不均匀
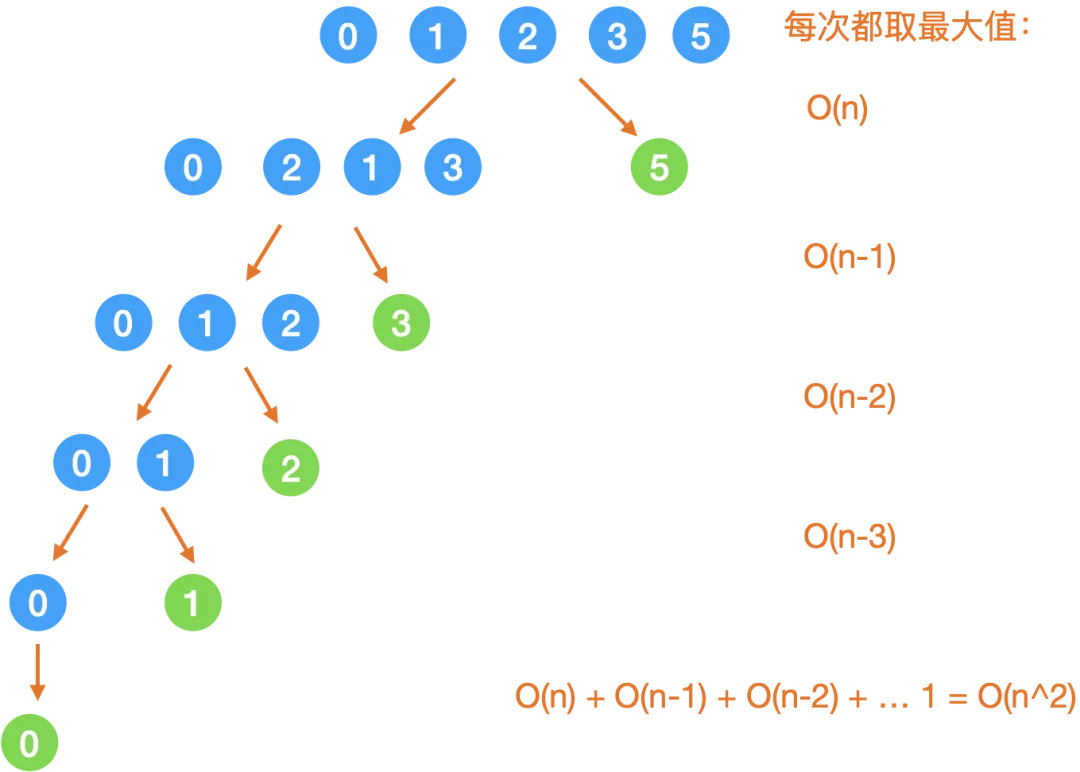
时间复杂度
空间复杂度
3. 总结
稳定性
最后
以上就是复杂狗为你收集整理的快速排序为什么这么快？的全部内容，希望文章能够帮你解决快速排序为什么这么快？所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复