参考的文章：
（1）这或许是东半球讲十大排序算法最好的一篇文章
（2）排序算法 - 面试中的排序算法总结
（3）必学十大经典排序算法，看这篇就够了

算法

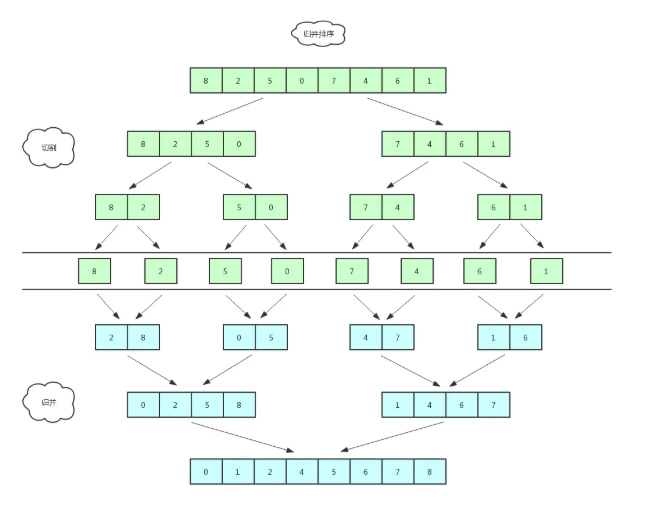
（1）归并排序的核心思想是分治，分而治之，将一个大问题分解成无数的小问题进行处理，处理之后再合并，这里我们采用递归来实现；
（2）时间复杂度O(nlogn)

代码1-递归

    /**
     * 正确的递归写法
     *
     * @param arr
     * @param left
     * @param right
     * @return
     */
	 public  int[] mergeSort2(int[] arr, int left, int right) {
        // 如果 left == right，表示数组只有一个元素，则不用递归排序
        if (left < right) {
            // 把大的数组分隔成两个数组
            int mid = (left + right) / 2;
            // 对左半部分进行排序
            arr = mergeSort2(arr, left, mid);
            // 对右半部分进行排序
            arr = mergeSort2(arr, mid + 1, right);
            //进行合并
            merge2(arr, left, mid, right);
        }
        return arr;
    }

    // 合并函数，把两个有序的数组合并起来
    // arr[left..mif]表示一个数组，arr[mid+1 .. right]表示一个数组
    private void merge2(int[] arr, int left, int mid, int right) {
        //先用一个临时数组把他们合并汇总起来
        int[] a = new int[right - left + 1];
        int i = left;
        int j = mid + 1;
        int k = 0;
        while (i <= mid && j <= right) {
            if (arr[i] < arr[j]) {
                a[k++] = arr[i++];
            } else {
                a[k++] = arr[j++];
            }
        }
        while(i <= mid) a[k++] = arr[i++];
        while(j <= right) a[k++] = arr[j++];
        // 把临时数组复制到原数组
        for (i = 0; i < k; i++) {
            arr[left++] = a[i];
        }
  }

代码2-非递归

    /**
     * 非递归写法
     * 
     * @param arr
     * @return
     */
    public static int[] mergeSort3(int[] arr) {
        int n = arr.length;
        // 子数组的大小分别为1，2，4，8...
        // 刚开始合并的数组大小是1，接着是2，接着4....
        for (int i = 1; i < n; i += i) {
            //进行数组进行划分
            int left = 0;
            int mid = left + i - 1;
            int right = mid + i;
            //进行合并，对数组大小为 i 的数组进行两两合并
            while (right < n) {
                // 合并函数和递归式的合并函数一样
                merge3(arr, left, mid, right);
                left = right + 1;
                mid = left + i - 1;
                right = mid + i;
            }
            // 还有一些被遗漏的数组没合并，千万别忘了
            // 因为不可能每个字数组的大小都刚好为 i
            if (left < n && mid < n) {
                merge3(arr, left, mid, n - 1);
            }
        }
        return arr;
    }

    private void merge3(int[] arr, int left, int mid, int right) {
        //先用一个临时数组把他们合并汇总起来
        int[] a = new int[right - left + 1];
        int i = left;
        int j = mid + 1;
        int k = 0;
        while (i <= mid && j <= right) {
            if (arr[i] < arr[j]) {
                a[k++] = arr[i++];
            } else {
                a[k++] = arr[j++];
            }
        }
        
        while(i <= mid) a[k++] = arr[i++];
        while(j <= right) a[k++] = arr[j++];
        // 把临时数组复制到原数组
        for (i = 0; i < k; i++) {
            arr[left++] = a[i];
        }
  }

最后

以上就是爱笑老师为你收集整理的十大经典排序算法——归并排序（Merge Sort）算法代码1-递归代码2-非递归的全部内容，希望文章能够帮你解决十大经典排序算法——归并排序（Merge Sort）算法代码1-递归代码2-非递归所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。