一、归并排序
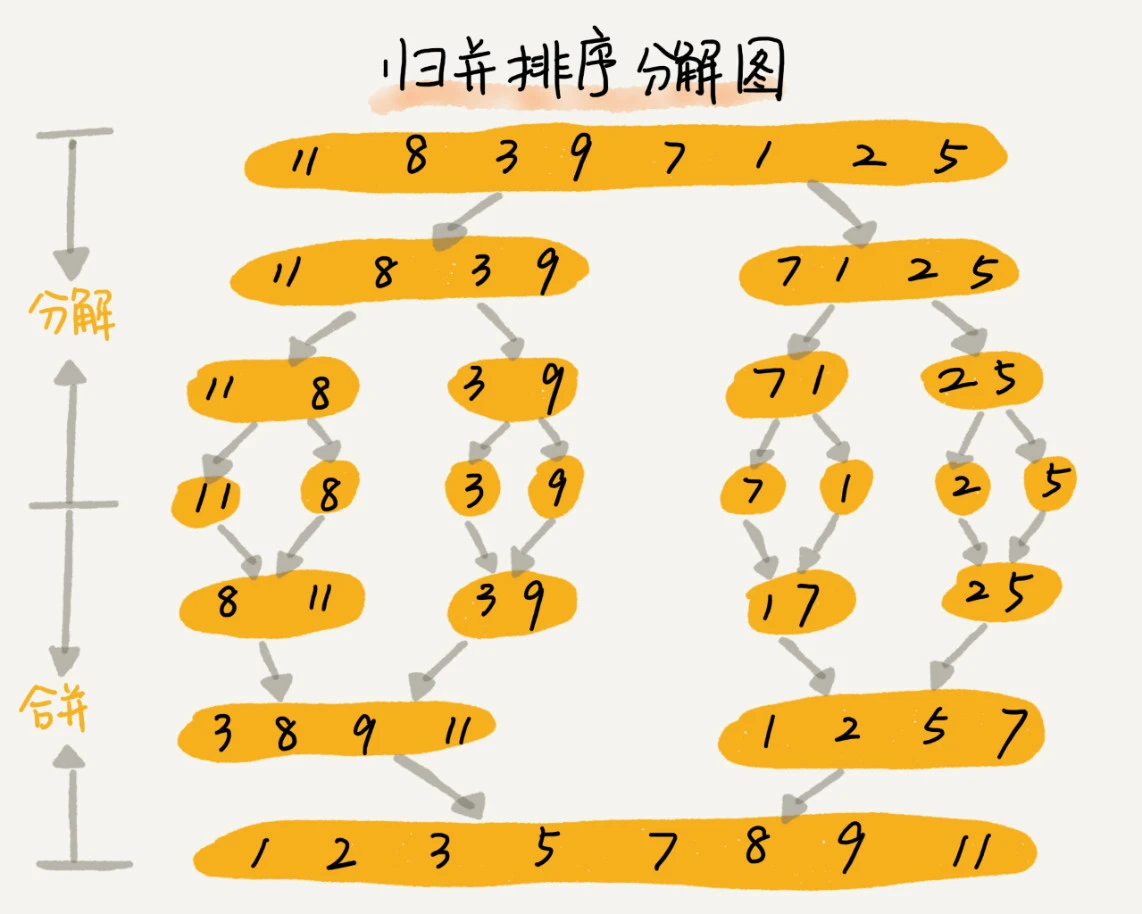
归并排序使用的就是分治思想。分治，顾名思义，就是分而治之，将一个大问题分解成小的子问题来解决。小的子问题解决了，大问题也就解决了。
1
2
3
4
5递推公式： merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r)) 终止条件： p >= r 不用再继续分解
代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36public void mergeSort(int[] a, int n){ merge(a, 0, n-1); } public void merge(int[] a, int l, int r){ if(l >= r){ return; } int mid = (l + r)/2; merge(a, l, mid); merge(a, mid + 1, r); merge(a, l, mid, mid +1, r); } public void merge(int[] a, int l1, int r1, int l2, int r2){ int[] temp = new int[r2 - l1 + 1]; int index = 0; int index1 = l1; int index2 = l2; while(index1 <= r1 && index2 <= r2){ if(a[index1] <= a[index2]){ temp[index++] = a[index1++]; }else{ temp[index++] = a[index2++]; } } while (index1 <= r1){ temp[index++] = a[index1++]; } while (index2 <= r2){ temp[index++] = a[index2++]; } for (int i=0;i<temp.length;++i){ a[l1 + i] = temp[i]; } }
结论：
是否稳定：是稳定排序算法
时间复杂度：
我们假设对 n 个元素进行归并排序需要的时间是 T(n)，那分解成两个子数组排序的时间都是 T(n/2)。我们知道，merge() 函数合并两个有序子数组的时间复杂度是 O(n)。所以，套用前面的公式，归并排序的时间复杂度的计算公式就是
1
2T(1) = C； n=1时，只需要常量级的执行时间，所以表示为C。 T(n) = 2*T(n/2) + n； n>1
1
2
3
4
5
6
7T(n) = 2*T(n/2) + n = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n ...... = 2^k * T(n/2^k) + k * n ......
通过这样一步一步分解推导，我们可以得到 T(n) = 2^kT(n/2^k)+kn。当 T(n/2^k)=T(1) 时，也就是 n/2^k=1，我们得到 k=log2n 。我们将 k 值代入上面的公式，得到 T(n)=Cn+nlog2n 。如果我们用大 O 标记法来表示的话，T(n) 就等于 O(nlogn)。所以归并排序的时间复杂度是 O(nlogn)。
所以不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)。
空间复杂度：尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以空间复杂度是 O(n)。
二、快速排序
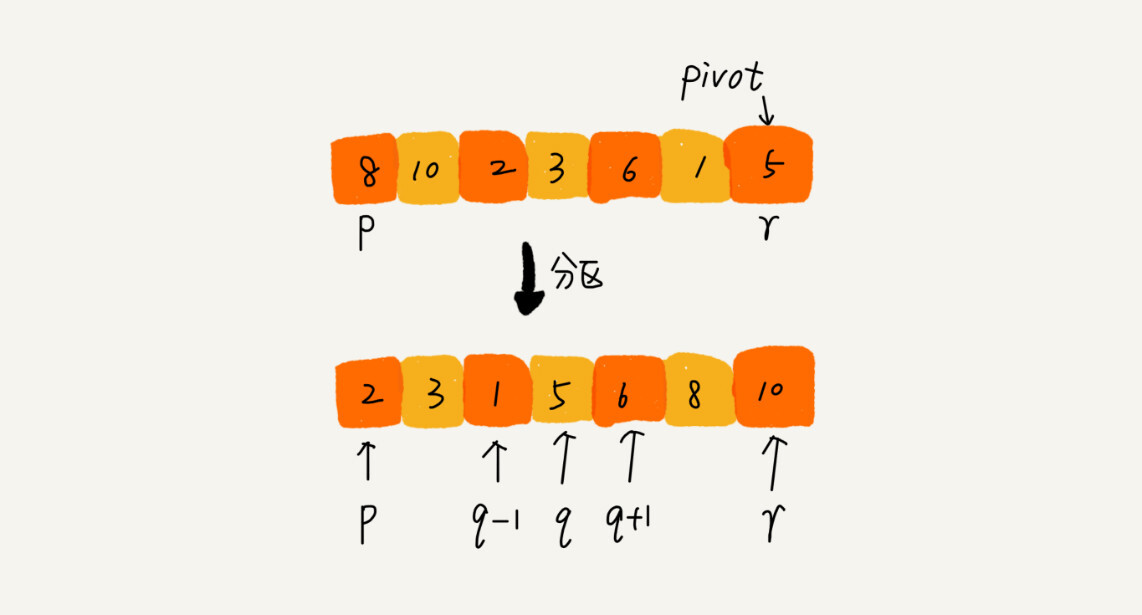
我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。
根据分治、递归的处理思想，我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了。
递推公式：
1
2
3
4
5递推公式： quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1… r) 终止条件： p >= r
代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28public void quickSort(int[] a, int n){ sort(a, 0, n-1); } private void sort(int[] a, int l, int r){ if(l >= r){ return; } int k = a[l]; int start = l, end = r; while(start < end){ while(start < end && a[end] >= k){ end--; } if(start < end){ a[start++] = a[end]; } while(start < end && a[start] <= k){ start++; } if(start < end){ a[end--] = a[start]; } } a[start] = k; sort(a, l, start-1); sort(a, start + 1, r); }
结论：
是否稳定：不稳定，涉及到交换了
是否原地排序：是， 空间复杂度是O(1)
时间复杂度：
1.利用归并排序所讲，假设每次递归都能正好将数组分为相等的2个小区间，那么时间复杂度也是O(nlogn)
2.如果数据是有序的，那么我们要分区n次，每次分区扫描n, n-1 ,n-2 ... 1个数据，也就是平均扫描（n/2）个数据,时间复杂度是O(n^2)
最好、平均时间复杂度是O（nlogn）,最坏是O(n^2)
三、总结
归并排序和快速排序是两种稍微复杂的排序算法，它们用的都是分治的思想，代码都通过递归来实现，过程非常相似。理解归并排序的重点是理解递推公式和 merge() 合并函数。同理，理解快排的重点也是理解递推公式，还有 partition() 分区函数。
最后
以上就是大意溪流最近收集整理的关于10 归并排序and快速排序一、归并排序二、快速排序三、总结的全部内容，更多相关10内容请搜索靠谱客的其他文章。
发表评论 取消回复