概述
一、实验目的
1.熟悉Matlab环境。
2.掌握 Matlab 中一些基本函数的建立方法
3.要求掌握频率域采样会引起时域周期化的概念
4.频率域采样定理及其对频域采样点数选择的指导作用
二、实验内容
(1)实验原理与方法
时域采样定理的要点是：
频域采样定理的要点是：
在数字信号处理的应用中，只要涉及时域或者频域采样，都必须服从这两个采样理论的要点。对比上面叙述的时域采样原理和频域采样原理，得到一个有用的结论，这两个采样理论具有对偶性：“时域采样频谱周期延拓，频域采样时域信号周期延拓”。因此放在一起进行实验。
(2)实验内容及步骤
1.编写程序，产生以下离散序列：
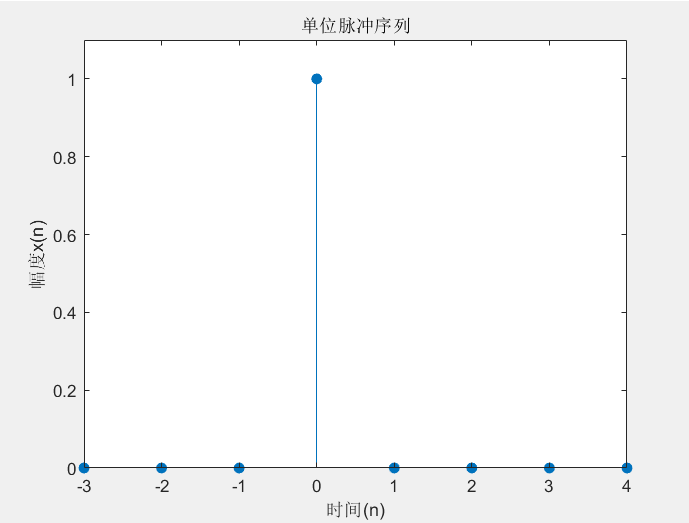
(1) % f(n)=δ(n) (-3<n<4)
clc
clear
n1=-3;n2=4;n0=0;
n=n1:n2;
x=[n==n0];
stem(n,x,'filled');
axis([n1,n2,0,1.1*max(x)]);
xlabel('时间(n)');
ylabel('幅度x(n)');
title('单位脉冲序列');
结果：
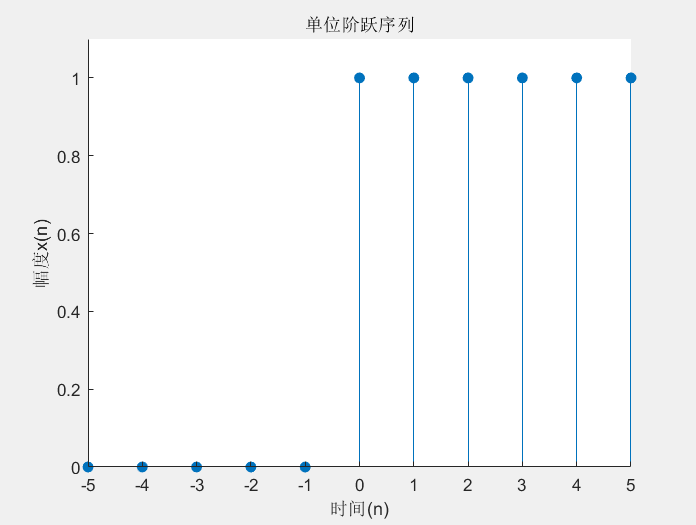
(2) %f(n)=u(n) (-5<n<5)
clc
clear
n1=-5;n2=5;n0=0;
n=n1:n2;
x=[n>=n0];
stem(n,x,'filled');
axis([n1,n2,0,1.1*max(x)]);
xlabel('时间(n)');
ylabel('幅度x(n)');
title('单位阶跃序列');
box
结果：
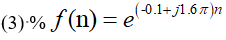
clc
clear
n1=16;a=-0.1;w=1.6*pi;
n=0:n1;
x=exp((a+j*w)*n);
subplot(2,2,1);
plot(n,real(x));
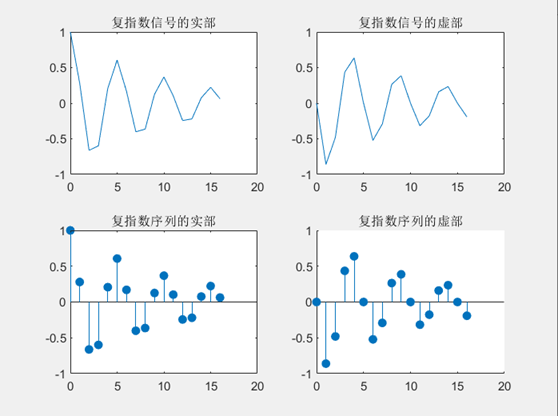
title('复指数信号的实部');
subplot(2,2,3);
stem(n,real(x),'filled');
title('复指数序列的实部');
subplot(2,2,2);
plot(n,imag(x));
title('复指数信号的虚部');
subplot(2,2,4);
stem(n,imag(x),'filled');
title('复指数序列的虚部');
box %box on
结果：
(4) %f(n)=3sin(nπ/4) (0<n<20); 能够算出来周期为8
f= 1/8;
Um=3;
nt=2; %显示的周期数目
N=32; T=1/f;
dt=T/N; %采样间隔
n=0:nt*N-1;
tn=n*dt;
x=Um*sin(2*f*pi*tn);
subplot(2,1,1);
plot(tn,x);
axis([0,nt*T,1.1*min(x),1.1*max(x)]);
ylabel('x(t)');
subplot(2,1,2);
stem(tn,x);
axis([0,nt*T,1.1*min(x),1.1*max(x)]);
ylabel('x(n)');
box on %对当前图形右边及上边加边框
结果：
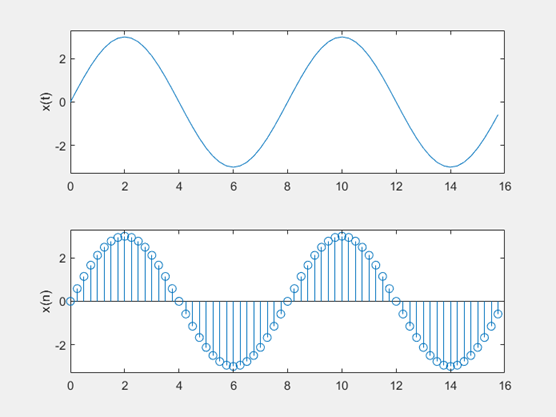
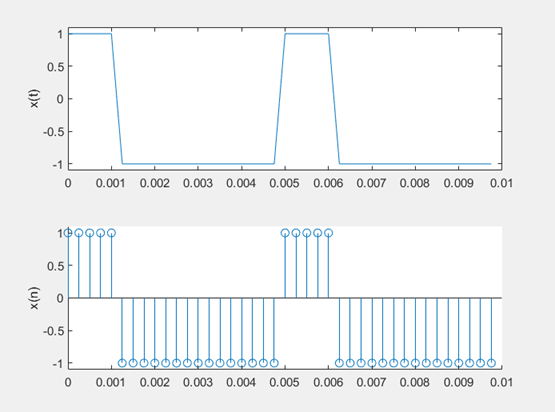
(5) 一个连续的周期性方波信号频率为200Hz，信号幅度在-1～+1V之间，要求在图形窗口上显示其两个周期的波形。以4kHz的频率对连续信号进行采样，编写程序生成连续信号和其采样获得的离散信号波形。
clc
clear
f=200;
nt=2; %显示周期数
N=20;T=1/f;
dt=T/N; %每个周期显示20个离散值，4kHz的频率
n=0:nt*N-1;tn=n*dt;
x=square(2*f*pi*tn,25); %其中25为占空比
subplot(2,1,1);
plot(tn,x);
axis([0,nt*T,1.1*min(x),1.1*max(x)]);
ylabel('x(t)');
subplot(2,1,2);
stem(tn,x);
axis([0,nt*T,1.1*min(x),1.1*max(x)]);
ylabel('x(n)');
box
结果：
(6) 时域采样理论的验证程序清单
clc
clear
% 时域采样理论验证程序exp1a.m
Tp=64/1000; %观察时间Tp=64微秒
%产生M长采样序列x(n)
% Fs=1000;T=1/Fs;
% M=Tp*Fs;n=0:M-1;
% Fs=300;T=1/Fs;
% M=Tp*Fs;n=0:M-1;
Fs=200;T=1/Fs;
M=Tp*Fs;n=0:M-1;
A=444.128;alph=pi*50*2^0.5;omega=pi*50*2^0.5;
xnt=A*exp(-alph*n*T).*sin(omega*n*T);
Xk=T*fft(xnt,M); %M点FFT[xnt)]
yn='xa(nT)';
subplot(3,2,5);
tstem(xnt,yn); %调用自编绘图函数tstem绘制序列图
box on;
title('(c) Fs=1000Hz');
k=0:M-1;fk=k/Tp;
subplot(3,2,6);
plot(fk,abs(Xk));
title('(c) T*FT[xa(nT)],Fs=1000Hz');
xlabel('f(Hz)');
ylabel('幅度');
axis([0,Fs,0,1.2*max(abs(Xk))])
%=================================================
function tstem(xn,yn)
%时域序列绘图函数
% xn:信号数据序列，yn:绘图信号的纵坐标名称（字符串）
n=0:length(xn)-1;
stem(n,xn,'.');
box on
xlabel('n');
ylabel(yn);
axis([0,n(end),min(xn),1.2*max(xn)])
end
结果：
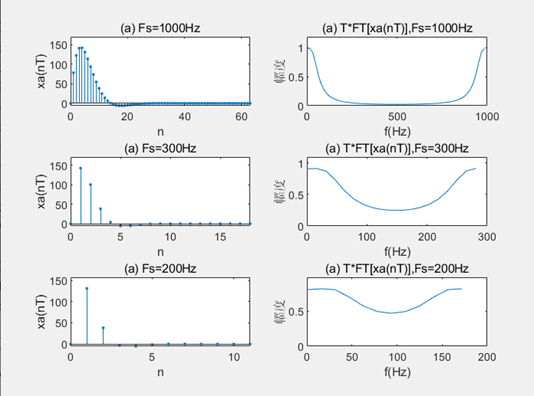
如图所示可见，采样序列的频谱的确是以采样频率为周期对模拟信号频谱的周期延拓。当采样频率为1000Hz时频谱混叠很小；当采样频率为300Hz时，在折叠频率150Hz附近频谱混叠很严重；当采样频率为200Hz时，在折叠频率110Hz附近频谱混叠更很严重。
频域采样理论的验证程序清单
clc
clear
%频域采样理论验证程序exp1b.m
M=27;N=32;n=0:M;
%产生M长三角波序列x(n)
xa=0:floor(M/2);
xb= ceil(M/2)-1:-1:0;
xn=[xa,xb];
Xk=fft(xn,1024); %1024点FFT[x(n)], 用于近似序列x(n)的TF
X32k=fft(xn,32); %32点FFT[x(n)]
x32n=ifft(X32k); %32点IFFT[X32(k)]得到x32(n)
X16k=X32k(1:2:N); %隔点抽取X32k得到X16(K)
x16n=ifft(X16k,N/2);%16点IFFT[X16(k)]得到x16(n)
subplot(3,2,2);stem(n,xn,'.');
box on
title('(b) 三角波序列x(n)');
xlabel('n');
ylabel('x(n)');
axis([0,32,0,20])
k=0:1023;wk=2*k/1024; %
subplot(3,2,1);
plot(wk,abs(Xk));
title('(a)FT[x(n)]');
xlabel('omega/pi');
ylabel('|X(e^j^omega)|');
axis([0,1,0,200])
k=0:N/2-1;
subplot(3,2,3);
stem(k,abs(X16k),'.');
box on
title('(c) 16点频域采样');
xlabel('k');
ylabel('|X_1_6(k)|');
axis([0,8,0,200])
n1=0:N/2-1;
subplot(3,2,4);
stem(n1,x16n,'.');
box on
title('(d) 16点IDFT[X_1_6(k)]');
xlabel('n');
ylabel('x_1_6(n)');
axis([0,32,0,20])
k=0:N-1;
subplot(3,2,5);
stem(k,abs(X32k),'.');
box on
title('(e) 32点频域采样');
xlabel('k');
ylabel('|X_3_2(k)|');
axis([0,16,0,200])
n1=0:N-1;
subplot(3,2,6);
stem(n1,x32n,'.');box on
title('(f) 32点IDFT[X_3_2(k)]');
xlabel('n');
ylabel('x_3_2(n)');
axis([0,32,0,20])
结果：
tstem 程序清单
%=======================tstem 程序清单====================
function tstem(xn,yn)
%时域序列绘图函数
% xn:信号数据序列，yn:绘图信号的纵坐标名称（字符串）
n=0:length(xn)-1;
stem(n,xn,'.');box on
xlabel('n');ylabel(yn);
axis([0,n(end),min(xn),1.2*max(xn)])
三、实验总结
实验结果说明什么？
时域采样理论的验证结果：
由程序运行结果图6可见，采样序列的频谱的确是以采样频率为周期对模拟信号频谱的周期延拓。当采样频率为1000Hz时频谱混叠很小；当采样频率为300Hz时，在折叠频率150Hz附近频谱混叠很严重；当采样频率为200Hz时，在折叠频率110Hz附近频谱混叠更很严重。
频域采样理论的验证的结果：
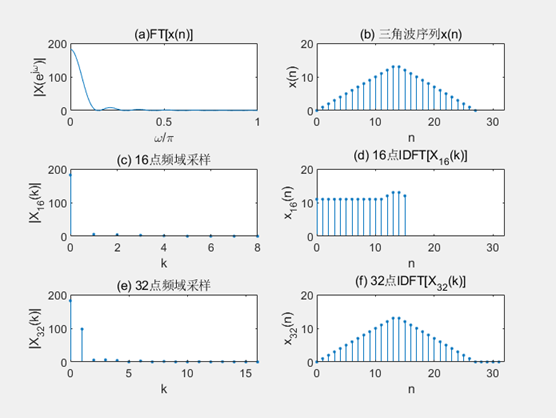
该图验证了频域采样理论和频域采样定理。对信号x(n)的频谱函数X(e^jω)在[0，2π]上等间隔采样N=16时， N点IDFT[]得到的序列正是原序列x(n)以16为周期进行周期延拓后的主值区序列：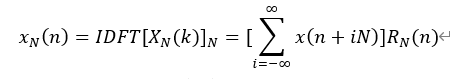
由于N<M，所以发生了时域混叠失真，因此。与x(n)不相同，如图7（c）和（d）所示。当N=32时，如图7（c）和（d）所示，由于N>M，频域采样定理，所以不存在时域混叠失真，因此与x(n)相同。
最后
以上就是故意钢笔为你收集整理的数字信号处理(DSP)实验——离散信号产生及频谱的绘制的全部内容，希望文章能够帮你解决数字信号处理(DSP)实验——离散信号产生及频谱的绘制所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复